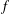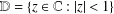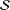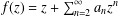Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shi, Lei
and
Arif, Muhammad
2023.
Sharp bounds on the third Hankel determinant for the Ozaki close-to-convex and convex functions.
Lithuanian Mathematical Journal,
Vol. 63,
Issue. 4,
p.
487.