Published online by Cambridge University Press: 21 February 2012
Let p be an odd prime. In this paper, we consider the equation 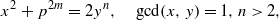 and we describe all its solutions. Moreover, we prove that this equation has no solution (x,y,m,n) when n>3 is an odd prime and y is not the sum of two consecutive squares. This extends the work of Tengely [On the diophantine equation x2+q2m=2yp, Acta Arith.127(1) (2007), 71–86].
and we describe all its solutions. Moreover, we prove that this equation has no solution (x,y,m,n) when n>3 is an odd prime and y is not the sum of two consecutive squares. This extends the work of Tengely [On the diophantine equation x2+q2m=2yp, Acta Arith.127(1) (2007), 71–86].
The first author was partly supported by the Fundamental Research Funds for the Central Universities (No. 2011121039). The second author was supported by the National Science Foundation of China (No. 10971184). The third author was supported by Purdue University North Central.