Article contents
PRIME-UNIVERSAL DIAGONAL QUADRATIC FORMS
Published online by Cambridge University Press: 05 October 2020
Abstract
A (positive definite and integral) quadratic form is said to be prime-universal if it represents all primes. Recently, Doyle and Williams [‘Prime-universal quadratic forms 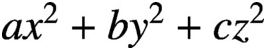 $ax^2+by^2+cz^2$ and
$ax^2+by^2+cz^2$ and 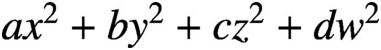 $ax^2+by^2+cz^2+dw^2$’, Bull. Aust. Math. Soc. 101 (2020), 1–12] classified all prime-universal diagonal ternary quadratic forms and all prime-universal diagonal quaternary quadratic forms under two conjectures. We classify all prime-universal diagonal quadratic forms regardless of rank, and prove the so-called 67-theorem for a diagonal quadratic form to be prime-universal.
$ax^2+by^2+cz^2+dw^2$’, Bull. Aust. Math. Soc. 101 (2020), 1–12] classified all prime-universal diagonal ternary quadratic forms and all prime-universal diagonal quaternary quadratic forms under two conjectures. We classify all prime-universal diagonal quadratic forms regardless of rank, and prove the so-called 67-theorem for a diagonal quadratic form to be prime-universal.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (NRF-2019R1F1A1064037), the third author was supported by an NRF grant funded by MSIT (NRF-2020R1I1A1A01055225), the fourth author was supported by the NRF (NRF-2019R1A6A3A01096245) and the fifth author was supported by the NRF grant funded by MSIT (NRF-2020R1A5A1016126).
References
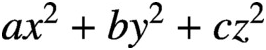 $a{x}^2+b{y}^2+c{z}^2$
and
$a{x}^2+b{y}^2+c{z}^2$
and
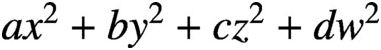 $a{x}^2+b{y}^2+c{z}^2+d{w}^2$
’, Bull. Aust. Math. Soc. 101 (2020), 1–12.10.1017/S0004972719001023CrossRefGoogle Scholar
$a{x}^2+b{y}^2+c{z}^2+d{w}^2$
’, Bull. Aust. Math. Soc. 101 (2020), 1–12.10.1017/S0004972719001023CrossRefGoogle Scholar- 2
- Cited by


