Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T09:01:06.679Z Has data issue: false hasContentIssue false
  • English
  • Français

QUENCHED CENTRAL LIMIT THEOREM FOR DVORETZKY COVERING

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  28 January 2025

YUANYANG CHANG Open the ORCID record for YUANYANG CHANG [Opens in a new window]  and
PING LIU Open the ORCID record for PING LIU [Opens in a new window]
YUANYANG CHANG
Affiliation:
Department of Mathematics, Wuhan University of Technology, Wuhan 430070, P. R. China e-mail: changyy@whut.edu.cn
PING LIU*
Affiliation:
Department of Mathematics, Wuhan University of Technology, Wuhan 430070, P. R. China
*
e-mail: 1724796906@qq.com
Get access Rights & Permissions [Opens in a new window]

Abstract

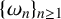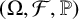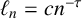Let $\{\omega _n\}_{n\geq 1}$ be a sequence of independent and identically distributed random variables on a probability space $(\Omega , \mathcal {F}, \mathbb {P})$, each uniformly distributed on the unit circle $\mathbb {T}$, and let $\ell _n=cn^{-\tau }$ for some 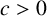$c>0$ and 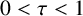$0<\tau <1$. Let $I_{n}=(\omega _n,\omega _n+\ell _n)$ be the random interval with left endpoint 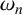$\omega _n$ and length 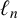$\ell _n$. We study the asymptotic property of the covering time 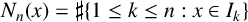$N_n(x)=\sharp \{1\leq k\leq n: x\in I_k\}$ for each 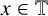$x\in \mathbb {T}$. We prove the quenched central limit theorem for the covering time, that is, 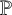$\mathbb {P}$-almost surely,

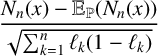$$ \begin{align*}\frac{N_n(x)-\mathbb{E}_{\mathbb{P}}(N_n(x))}{\sqrt{\sum_{k=1}^n \ell_k(1-\ell_k)}}\end{align*} $$

converges in law to the standard normal distribution.

Keywords

quenched central limit theoremDvoretzky covering

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 60F05: Central limit and other weak theorems

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 368 - 378
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work is supported by NSFC 11901204 and 12271418.

References

Abdelkader, M. and Aimino, R., ‘On the quenched central limit theorem for random dynamical systems’, J. Phys. A 49(24) (2016), Article no. 244002, 13 pages.CrossRefGoogle Scholar
Aimino, R., Nicol, M. and Vaienti, S., ‘Annealed and quenched limit theorems for random expanding dynamical systems’, Probab. Theory Related Fields 162(1–2) (2015), 233–274.CrossRefGoogle Scholar
Ayyer, A., Liverani, C. and Stenlund, M., ‘Quenched CLT for random toral automorphism’, Discrete Contin. Dyn. Syst. 24(2) (2009), 331–348.CrossRefGoogle Scholar
Barral, J. and Fan, A. H., ‘Covering numbers of different points in Dvoretzky covering’, Bull. Sci. Math. 129 (2005), 275–317.CrossRefGoogle Scholar
Dvoretzky, A., ‘On covering a circle by randomly placed arcs’, Proc. Natl. Acad. Sci. USA 42 (1956), 199–203.CrossRefGoogle ScholarPubMed
Ekström, F. and Persson, T., ‘Hausdorff dimension of random limsup sets’, J. Lond. Math. Soc. (2) 98(3) (2018), 661–686.CrossRefGoogle Scholar
Fan, A. H., Décompositions de mesures et recouvrements aléatoires, Ph.D. Thesis, University of Paris-Sud, 1989 (Publications Mathématiques d’Orsay, 89-05).Google Scholar
Fan, A. H., ‘How many intervals cover a point in Dvoretzky covering?’, Israel J. Math. 131 (2002), 157–184.CrossRefGoogle Scholar
Fan, A. H. and Kahane, J. P., ‘Rareté des intervalles recouvrant un point dans un recouvrement alatoire’, Ann. Inst. Henri Poincaré Probab. Stat. 29(3) (1993), 453–466.Google Scholar
Fan, A. H. and Karagulyan, D., ‘On $\mu$ -Dvoretzky random covering of the circle’, Bernoulli 27(2) (2021), 1270–1290.CrossRefGoogle Scholar
Fan, A. H., Schmeling, J. and Troubetzkoy, S., ‘A multifractal mass transference principle for Gibbs measures with applications to dynamical Diophantine approximation’, Proc. Lond. Math. Soc. (3) 107(5) (2013), 1173–1219.CrossRefGoogle Scholar
Fan, A. H. and Wu, J., ‘On the covering by small random intervals’, Ann. Inst. Henri Poincaré Probab. Stat. 40(1) (2004), 125–131.CrossRefGoogle Scholar
Feng, D. J., Järvenpää, E., Järvenpää, M. and Suomala, V., ‘Dimensions of random covering sets in Riemann manifolds’, Ann. Probab. 46(3) (2018), 1542–1596.CrossRefGoogle Scholar
Hu, Z. N. and Li, B., ‘Random covering sets in metric space with exponentially mixing property’, Statist. Probab. Lett. 168 (2021), Article no. 108922, 7 pages.CrossRefGoogle Scholar
Järvenpää, E., Järvenpää, M., Koivusalo, H., Li, B. and Suomala, V., ‘Hausdorff dimension of affine random covering sets in torus’, Ann. Inst. Henri Poincaré Probab. Stat. 50 (2014), 1371–1384.CrossRefGoogle Scholar
Järvenpää, E., Järvenpää, M., Koivusalo, H., Li, B., Suomala, V. and Xiao, Y. M., ‘Hitting probabilities of random covering sets in tori and metric spaces’, Electron. J. Probab. 22(1) (2017), 1–18.CrossRefGoogle Scholar
Kahane, J. P., Some Random Series of Functions (Cambridge University Press, Cambridge, 1985).Google Scholar
Kifer, Y., ‘Limit theorems for random transformations and processes in random environments’, Trans. Amer. Math. Soc. 350 (1998), 1481–1518.CrossRefGoogle Scholar
Petrov, V. V., Limit Theorems of Probability Theory, Oxford Studies in Probability, 4 (The Clarendon Press, Oxford, 1995).Google Scholar
Seuret, S., ‘Inhomogeneous random coverings of topological Markov shifts’, Math. Proc. Cambridge Philos. Soc. 165(2) (2018), 341–357.CrossRefGoogle Scholar
Shepp, L., ‘Covering the circle with random arcs’, Israel J. Math. 11 (1972), 328–345.CrossRefGoogle Scholar