Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koizumi, Shin
2013.
An analogue of the spectral projection for homogeneous trees.
Hiroshima Mathematical Journal,
Vol. 43,
Issue. 2,
Colin de Verdière, Yves
and
Truc, Françoise
2013.
Scattering theory for graphs isomorphic to a regular tree at infinity.
Journal of Mathematical Physics,
Vol. 54,
Issue. 6,
Le Masson, Etienne
2014.
Pseudo-Differential Calculus on Homogeneous Trees.
Annales Henri Poincaré,
Vol. 15,
Issue. 9,
p.
1697.
Anantharaman, Nalini
and
Le Masson, Etienne
2015.
Quantum ergodicity on large regular graphs.
Duke Mathematical Journal,
Vol. 164,
Issue. 4,
Koizumi, Shin
2017.
A Paley–Wiener theorem for the spectral projection of symmetric graphs.
Pacific Journal of Mathematics,
Vol. 290,
Issue. 1,
p.
117.
Anantharaman, Nalini
2017.
Quantum Ergodicity on Regular Graphs.
Communications in Mathematical Physics,
Vol. 353,
Issue. 2,
p.
633.
Celotto, Dario
and
Meda, Stefano
2018.
On the analogue of the Fefferman–Stein theorem on graphs with the Cheeger property.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 197,
Issue. 5,
p.
1637.
Fernández-Bertolin, Aingeru
and
Jaming, Philippe
2020.
Uniqueness for solutions of the Schrödinger equation on trees.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 199,
Issue. 2,
p.
681.
Kumar, Pratyoosh
and
Rano, Sumit Kumar
2021.
A characterization of weak Lp-eigenfunctions of the Laplacian on homogeneous trees.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 200,
Issue. 2,
p.
721.
Rano, Sumit Kumar
2022.
A theorem of Roe and Strichartz on homogeneous trees.
Forum Mathematicum,
Vol. 34,
Issue. 1,
p.
115.
Mondal, Shyam Swarup
2022.
Boundedness and nuclearity of pseudo-differential operators on homogeneous trees.
Analysis and Mathematical Physics,
Vol. 12,
Issue. 3,
Rano, Sumit Kumar
2025.
Eigenfunctions of the Laplacian Satisfying Hardy-Type Estimates on Homogeneous Trees.
Potential Analysis,
Vol. 63,
Issue. 2,
p.
579.
Rano, Sumit Kumar
and
Sarkar, Rudra P.
2025.
A theorem of Strichartz for multipliers on homogeneous trees.
Mathematische Zeitschrift,
Vol. 309,
Issue. 1,

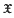 be a homogeneous tree,
be a homogeneous tree, 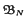 be the closed ball of radius
be the closed ball of radius 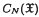 , the space of functions supported in
, the space of functions supported in 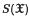 , the space of rapidly decreasing functions on
, the space of rapidly decreasing functions on 