Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Katz, Nicholas
and
Sarnak, Peter
1999.
Zeroes of zeta functions and symmetry.
Bulletin of the American Mathematical Society,
Vol. 36,
Issue. 1,
p.
1.
Bays, Carter
Ford, Kevin
Hudson, Richard H
and
Rubinstein, Michael
2001.
Zeros of Dirichlet L-functions near the Real Axis and Chebyshev's Bias.
Journal of Number Theory,
Vol. 87,
Issue. 1,
p.
54.
Miller, S. J.
2010.
A Symplectic Test of the L-Functions Ratios Conjecture.
International Mathematics Research Notices,
Goes, John
Jackson, Steven
Miller, Steven J.
Montague, David
Ninsuwan, Kesinee
Peckner, Ryan
and
Pham, Thuy
2010.
A unitary test of the Ratios Conjecture.
Journal of Number Theory,
Vol. 130,
Issue. 10,
p.
2238.
Huynh, Duc Khiem
Miller, Steven J.
and
Morrison, Ralph
2011.
An elliptic curve test of the L-Functions Ratios Conjecture.
Journal of Number Theory,
Vol. 131,
Issue. 6,
p.
1117.
Miller, Steven J.
and
Peckner, Ryan
2012.
Low-lying zeros of number field L -functions.
Journal of Number Theory,
Vol. 132,
Issue. 12,
p.
2866.
Entin, Alexei
Roditty-Gershon, Edva
and
Rudnick, Zeév
2013.
Low-lying Zeros of Quadratic Dirichlet L-Functions, Hyper-elliptic Curves and Random Matrix Theory.
Geometric and Functional Analysis,
Vol. 23,
Issue. 4,
p.
1230.
Alpoge, L.
and
Miller, S. J.
2014.
Low-Lying Zeros of Maass Form L-Functions.
International Mathematics Research Notices,
Alpoge, Levent
Amersi, Nadine
Iyer, Geoffrey
Lazarev, Oleg
Miller, Steven J.
and
Zhang, Liyang
2015.
Analytic Number Theory.
p.
19.
Barrett, Owen
Firk, Frank W. K.
Miller, Steven J.
and
Turnage-Butterbaugh, Caroline
2016.
Open Problems in Mathematics.
p.
123.
Mackall, Blake
Miller, Steven J.
Rapti, Christina
Turnage-Butterbaugh, Caroline
and
Winsor, Karl
2016.
Families of Automorphic Forms and the Trace Formula.
p.
435.
Sarnak, Peter
Shin, Sug Woo
and
Templier, Nicolas
2016.
Families of Automorphic Forms and the Trace Formula.
p.
531.
Barrett, Owen
Burkhardt, Paula
DeWitt, Jonathan
Dorward, Robert
and
Miller, Steven J.
2017.
One-level density for holomorphic cusp forms of arbitrary level.
Research in Number Theory,
Vol. 3,
Issue. 1,
Fiorilli, Daniel
Parks, James
and
Södergren, Anders
2017.
Low-lying zeros of quadratic Dirichlet -functions: lower order terms for extended support.
Compositio Mathematica,
Vol. 153,
Issue. 6,
p.
1196.
Andrade, Julio
and
Baluyot, Siegfred
2020.
Small zeros of Dirichlet L-functions of quadratic characters of prime modulus.
Research in Number Theory,
Vol. 6,
Issue. 2,
Lesesvre, Didier
2022.
Low-lying zeros of L-functions for Quaternion Algebras.
Annales de l'Institut Fourier,
Vol. 71,
Issue. 4,
p.
1635.
Bołdyriew, Elżbieta
Chen, Fangu
Devlin, Charles
Miller, Steven J.
and
Zhao, Jason
2023.
Determining optimal test functions for 2-level densities.
Research in Number Theory,
Vol. 9,
Issue. 2,
Lin, Hua
2024.
One-level density of zeros of Dirichlet L-functions over function fields.
Journal of Number Theory,
Vol. 258,
Issue. ,
p.
368.
Holm, Kristian
2025.
The 1-Level Density for Zeros of Hecke L-Functions of Imaginary Quadratic Number Fields of Class Number 1.
Journal de théorie des nombres de Bordeaux,
Vol. 37,
Issue. 1,
p.
237.

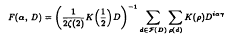
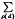 denotes the sum over the non-trivial zeros
denotes the sum over the non-trivial zeros 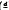 ) is the Kronecker symbol. The outer sum
) is the Kronecker symbol. The outer sum  is over all fundamental discriminants
is over all fundamental discriminants