No CrossRef data available.
Article contents
SOLVABLE GROUPS WHOSE NONNORMAL SUBGROUPS HAVE FEW ORDERS
Part of:
Representation theory of groups
Published online by Cambridge University Press: 27 December 2023
Abstract
Suppose that G is a finite solvable group. Let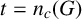 
$t=n_c(G)$ denote the number of orders of nonnormal subgroups of G. We bound the derived length 
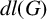$dl(G)$ in terms of 
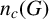$n_c(G)$. If G is a finite p-group, we show that 
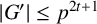$|G'|\leq p^{2t+1}$ and 
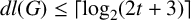$dl(G)\leq \lceil \log _2(2t+3)\rceil $. If G is a finite solvable nonnilpotent group, we prove that the sum of the powers of the prime divisors of 
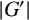$|G'|$ is less than t and that 
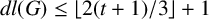$dl(G)\leq \lfloor 2(t+1)/3\rfloor +1$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 110 , Issue 1 , August 2024 , pp. 121 - 128
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This research is supported by the National Natural Science Foundation of China (Nos. 11971391, 12071376), by Fundamental Research Funds for the Central Universities (SWU-XDJH202305) and the Postgraduate Research and Innovation Project of Southwest University (SWUB23034).
References
An, L. J., ‘Finite
$p$
-groups whose non-normal subgroups have few orders’, Front. Math. China 13(4) (2018), 763–777.Google Scholar
$p$
-groups whose non-normal subgroups have few orders’, Front. Math. China 13(4) (2018), 763–777.Google ScholarBerkovich, Y., Groups of Prime Power Order, De Gruyter Expositions in Mathematics, 1 (Walter de Gruyter, Berlin, 2008).Google Scholar
Brandl, R., ‘Groups with few non-normal subgroups’, Comm. Algebra 23(6) (1995), 2091–2098.Google Scholar
Brandl, R., ‘Non-soluble groups with few conjugacy classes of non-normal subgroups’, Beitr. Algebra Geom. 54(2) (2013), 493–501.Google Scholar
Chen, G. Y. and Chen, S. M., ‘A note on the solvability of a finite group and the number of conjugate classes of its non-normal subgroups’, Southeast Asian Bull. Math. 34(4) (2010), 625–628.Google Scholar
Dedekind, R., ‘Üeber Gruppen, deren sämmtliche Theiler Normaltheiler sind’, Math. Ann. 48 (1897), 548–561.CrossRefGoogle Scholar
Gong, L., Cao, H. P. and Chen, G. Y., ‘Finite nilpotent groups having exactly four conjugacy classes of non-normal subgroups’, Algebra Colloq. 20(4) (2013), 579–592.Google Scholar
Kurzweil, H. and Stellmacher, B., The Theory of Finite Groups. An Introduction, Universitext (Springer-Verlag, New York, 2004); translated from the 1998 German original.Google Scholar
Mousavi, H., ‘On finite groups with few non-normal subgroups’, Comm. Algebra 27(7) (1999), 3143–3151.CrossRefGoogle Scholar
Mousavi, H., ‘Nilpotent groups with three conjugacy classes of non-normal subgroups’, Bull. Iranian Math. Soc. 40(5) (2014), 1291–1300.Google Scholar
Mousavi, H., ‘Non-nilpotent groups with three conjugacy classes of non-normal subgroups’, Int. J. Group Theory 3(2) (2014), 1–7.Google Scholar
Zhang, J. Q., ‘Finite groups all of whose non-normal subgroups possess the same order’, J. Algebra Appl. 11(3) (2012), Article no. 1250053, 7 pages.CrossRefGoogle Scholar