Hostname: page-component-cb9f654ff-w5vf4 Total loading time: 0 Render date: 2025-08-31T08:03:46.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants for metabelian groups of prime power exponent, colorings, and stairs

Part of: Algebraic combinatorics Representation theory of groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  10 December 2021

Jonathan Ariel Barmak
Jonathan Ariel Barmak*
Affiliation:
Departamento de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Buenos Aires, Argentina Instituto de Investigaciones Matemáticas Luis A, Santaló (IMAS), CONICET-Universidad de Buenos Aires, Buenos Aires, Argentina
*
e-mail: jbarmak@dm.uba.ar
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the free metabelian group 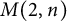$M(2,n)$ of prime power exponent n on two generators by means of invariants 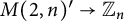$M(2,n)'\to \mathbb {Z}_n$ that we construct from colorings of the squares in the integer grid 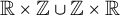$\mathbb {R} \times \mathbb {Z} \cup \mathbb {Z} \times \mathbb {R}$. In particular, we improve bounds found by Newman for the order of 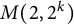$M(2,2^k)$. We study identities in 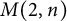$M(2,n)$, which give information about identities in the Burnside group 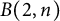$B(2,n)$ and the restricted Burnside group 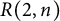$R(2,n)$.

Keywords

Burnside groupsmetabelian groupswinding invariantcoloringsidentities

MSC classification

Primary: 20F50: Periodic groups; locally finite groups
Secondary: 05E15: Combinatorial aspects of groups and algebras 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks 20F45: Engel conditions 20F70: Algebraic geometry over groups; equations over groups

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 1 , February 2023 , pp. 267 - 297
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is supported by CONICET and partially supported by grants PICT-2017-2806, PIP 11220170100357CO, and UBACyT 20020160100081BA.

References

Adian, S. I., The Burnside problem and identities in groups (Nauka, Moscow, 1975), Springer, Berlin, 1979.CrossRefGoogle Scholar
Adian, S. I., New estimates of odd exponents of infinite Burnside groups . Proc. Steklov Inst. Math. 289(2015), 33–71.CrossRefGoogle Scholar
Adian, S. I. and Novikov, P. S., On infinite periodic groups I, II, III . Izv. Akad. Nauk SSSR. Ser. Mat. 32(1968), 212–244; 251–524; 709–731.Google Scholar
Alford, W. A., Havas, G., and Newman, M. F., Groups of exponent four . Notices Amer. Math. Soc. 22(1975), 301.Google Scholar
Allouche, J.-P. and Shallit, J., The ubiquitous Prouhet–Thue–Morse sequence . In: C. Ding, T. Helleseth, H. Niederreiter (eds.), Sequences and their applications (Singapore, 1998), Discrete Mathematics and Theoretical Computer Science, Springer, London, 1999, pp. 1–16.Google Scholar
Bachmuth, S., Heilbronn, H. A., and Mochizuki, H. Y., Burnside metabelian groups , Proc. R. Soc. Lond. Ser. A 307(1968), 235–250.Google Scholar
Barmak, J. A., A counterexample to a strong version of the Andrews–Curtis conjecture. Preprint, 2018. arXiv:1806.11493Google Scholar
Barmak, J. A., The winding invariant. Preprint, 2019. arXiv:1904.10072 Google Scholar
Bayes, A. J., Kautsky, J., and Wamsley, J. W., Computation in nilpotent groups (application) . In: M. F. Newman (ed.), Proceedings of the Second International Conference on the Theory of Groups (Canberra 1973), Lecture Notes in Mathematics, 372, Springer, Berlin, 1974, pp. 82–89.Google Scholar
Boffa, M. and Point, F., Identités de Thue–Morse dans les groupes . C. R. Acad. Sci. Paris Sér. I 312(1991), 667–670.Google Scholar
Bruck, R. H.. On the restricted Burnside problem . Arch. Math. (Basel) 13(1962), 179–186.CrossRefGoogle Scholar
Burnside, W., On an unsettled question in the theory of discontinuous groups . Q. J. Pure Appl. Math. 33(1902), 230–238.Google Scholar
Dark, R. S. and Newell, M. L.. On 2-generator metabelian groups of prime power exponent . Arch. Math. (Basel) 37(1982), 385–400.CrossRefGoogle Scholar
GAP Group, GAP—Groups, algorithms, and programming, version 4.10.2. 2019. https://www.gap-system.org.Google Scholar
Glauberman, G., Krause, E. F., and Struik, R. R., Engel congruences in groups of prime-power exponent . Canad. J. Math. 18(1966), 579–588.Google Scholar
Groves, D. and Vaughan-Lee, M., Finite groups of bounded exponent . Bull. Lond. Math. Soc. 35(2003), 37–40.CrossRefGoogle Scholar
Grunewald, F. J., Havas, G., Mennicke, J. L., and Newman, M. F., Groups of exponent 8 . Bull. Aust. Math. Soc. 20(1979), 7–16.Google Scholar
Gupta, N. D. and Newman, M. F., Engel congruences in groups of prime-power exponent . Canad. J. Math. 20(1968), 1321–1323.CrossRefGoogle Scholar
Gupta, N. D., Newman, M. F., and Tobin, S. J., On metabelian groups of prime-power exponent . Proc. R. Soc. Lond. Ser. A 302(1968), 237–242.Google Scholar
Gupta, N. D. and Tobin, S. J., On certain groups with exponent four . Math. Z. 102(1967), 216–226.Google Scholar
Hall, M. Jr, Solution of the Burnside problem for exponent six . Illinois J. Math. 2(1958), 764–786.CrossRefGoogle Scholar
Hall, M. Jr, The theory of groups, New York, Macmillan, 1959.Google Scholar
Hall, P. and Higman, G., On the p-length of p-soluble groups and reduction theorems for Burnside’s problem . Proc. Lond. Math. Soc. (3) 6(1956), 1–42.Google Scholar
Havas, G. and Newman, M. F., Application of computers to questions like those of Burnside . In: Burnside groups (Proceedings of a Workshop Held at the University of Bielefeld, Germany, June–July 1977), Lecture Notes in Mathematics, 806, Springer, Berlin–Heidelberg–New York, 1980, pp. 211–230.Google Scholar
Havas, G., Wall, G. E., and Wamsley, J. W., The two generator restricted Burnside group of exponent five . Bull. Aust. Math. Soc. 10(1974), 459–470.CrossRefGoogle Scholar
Hermanns, F.-J., Eine metabelsche Gruppe vom Exponenten 8 . Arch. Math. (Basel) 29(1977), 375–382.CrossRefGoogle Scholar
Ivanov, S. V., The free Burnside groups of sufficiently large exponents . Internat. J. Algebra Comput. 4(1994), nos. 1–2, 1–308.CrossRefGoogle Scholar
Khukhro, E. I. and Mazurov, V. D. (eds.). Unsolved problems in group theory, The Kourovka Notebook, 19, Institute of Mathematics, SO RAN, Novosibirsk, 2018. http://math.nsc.ru/~alglog/19tkt.pdf.Google Scholar
Kostrikin, A. I., On Burnside’s problem . Dokl. Akad. Nauk SSSR (N.S.) 119(1958), 1081–1084.Google Scholar
Kostrikin, A. I., The Burnside problem . Izv. Akad. Nauk SSSR Ser. Mat. 23(1959), 3–34; Amer. Math. Soc. Transl. (2) 36(1964), 63–99.Google Scholar
Kostrikin, A. I., On Engel properties of groups with the identical relation ${x}^{p^{\alpha }} = 1$ . Dokl. Akad. Nauk SSSR (N.S.) 35(1960), 524–526.Google Scholar
Kostrikin, A. I., Some related questions in the theory of groups and Lie algebras . In: M.F. Newman (ed.), Proceedings of the Second International Conference on the Theory of Groups, Canberra 1973, Lecture Notes in Mathematics, 372, Springer, Berlin, Heidelberg, 1974, pp. 409–416.Google Scholar
Kostrikin, A. I., Sandwiches in Lie algebras . Mat. Sb. (N.S.) 110(1979), no. 152, 3–12; Math. USSR Sb. 38(1981), 1–9.Google Scholar
Krause, E. F., Groups of exponent 8 satisfy the 14th Engel congruence . Proc. Amer. Math. Soc. 15(1964), 491–496.CrossRefGoogle Scholar
Levi, F. W., Groups in which the commutator operation satisfies certain algebraic conditions . J. Indian Math. Soc. (N.S.) 6(1942), 87–97.Google Scholar
Magnus, W., A connection between the Baker–Hausdorff formula and a problem of Burnside . Ann. of Math. (2) 52(1950), 111–126.CrossRefGoogle Scholar
Meier-Wunderli, H., Metabelsche Gruppen . Comment. Math. Helv. 25(1951), 1–10.CrossRefGoogle Scholar
Newman, M. F., Metabelian groups of prime-power exponent . In: Groups—Korea 1983, Lecture Notes in Mathematics, 1098, Springer, Berlin–Heidelberg–New York, 1984, pp. 87–98.CrossRefGoogle Scholar
Newman, M. F. and O’Brien, E. A., Application of computers to questions like those of Burnside, II . Internat. J. Algebra Comput. 6(1996), 593–605.Google Scholar
Nickel, W., NQ—a GAP package, version 2.5.4. 2019. https://www2.mathematik.tu-darmstadt.de/nickel/software/NQ/.Google Scholar
O’Brien, E. A. and Vaughan-Lee, M., The 2-generator restricted Burnside group of exponent 7 . Internat. J. Algebra Comput. 12(2002), no. 4, 575–592.CrossRefGoogle Scholar
Sanov, I. N., Solution of Burnside’s problem for exponent 4 . Uchen. Zap. Leningrad State Univ. Ser. Mat. 10(1940), 166–170.Google Scholar
Sanov, I. N., On a certain system of relations in periodic groups with period a power of a prime number . Izv. Akad. Nauk SSSR Ser. Mat. 15(1951), 477–502.Google Scholar
Shalev, A., Finite p-groups . In: Hartley, B., Seitz, G. M., Borovik, A. V., and Bryant, R. M. (eds.), Finite and locally finite groups (Proceedings of the NATO Advanced Study Institute held in Istanbul, August 14–27, 1974), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, 471, Kluwer Academic Publishers Group, Dodrecht, 1995, pp. 401–450.Google Scholar
Sims, C., Computation with finitely presented groups. Cambridge University Press, Cambridge, 1994.CrossRefGoogle Scholar
Skopin, A. I., Factors of the nilpotent series of certain metabelian groups of primary exponent . J. Math. Sci. (N.Y.) 30(1985), 1887–1912.CrossRefGoogle Scholar
Skopin, A. I., Investigation on the Besm-6 computer of the structure of the nilpotent series for the metabelian 2-generated group of exponent 27 . J. Sov. Math. 52(1990), 3185–3193.CrossRefGoogle Scholar
Struik, R. R., Notes on a paper by Sanov I . Proc. Amer. Math. Soc. 8(1957), 638–641.CrossRefGoogle Scholar
Vaughan-Lee, M. R., The restricted Burnside problem . Bull. Lond. Math. Soc. 17(1985), 113–133.CrossRefGoogle Scholar
Vaughan-Lee, M. R. and Zelmanov, E. I., Upper bounds in the restricted Burnside problem . J. Algebra 162(1993), 107–145.CrossRefGoogle Scholar
Vaughan-Lee, M. R. and Zelmanov, E. I., Upper bounds in the restricted Burnside problem, II . Internat. J. Algebra Comput. 6(1996) 735–744.CrossRefGoogle Scholar
Vaughan-Lee, M. R. and Zelmanov, E. I., Bounds in the restricted Burnside problem . J. Aust. Math. Soc. (Ser. A) 67(1999), 261–271.CrossRefGoogle Scholar
Zel’manov, E. I., The solution of the restricted Burnside problem for groups of odd exponent . lzv. Math. USSR 36(1991), 41–60.CrossRefGoogle Scholar
Zel’manov, E. I., The solution of the restricted Burnside problem for 2-groups . Mat. Sb. 182(1991), 568–592.Google Scholar