Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-31T13:02:29.880Z Has data issue: false hasContentIssue false
  • English
  • Français

Two general series identities involving modified Bessel functions and a class of arithmetical functions

Part of: Multiplicative number theory Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  10 October 2022

Bruce C. Berndt ,
Atul Dixit ,
Rajat Gupta  and
Alexandru Zaharescu
Bruce C. Berndt
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, IL 61801, USA e-mail: berndt@illinois.edu
Atul Dixit
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat 382355, India e-mail: adixit@iitgn.ac.in
Rajat Gupta*
Affiliation:
Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar, Gujarat 382355, India. Current address: Institute of Mathematics, Academia Sinica, 6F, Astronomy-Mathematics Building, No. 1, Sec. 4, Roosevelt Road, Taipei 106319, Taiwan
Alexandru Zaharescu
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, IL 61801, USA, and Institute of Mathematics of the Romanian Academy, P.O. Box 1-764, Bucharest RO-70700, Romania e-mail: zaharesc@illinois.edu
*
e-mail: rajatgpt@gate.sinica.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider two sequences 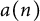$a(n)$ and 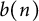$b(n)$, 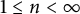$1\leq n<\infty $, generated by Dirichlet series

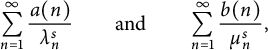$$ \begin{align*}\sum_{n=1}^{\infty}\frac{a(n)}{\lambda_n^{s}}\qquad\text{and}\qquad \sum_{n=1}^{\infty}\frac{b(n)}{\mu_n^{s}},\end{align*} $$

satisfying a familiar functional equation involving the gamma function 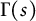$\Gamma (s)$. Two general identities are established. The first involves the modified Bessel function 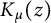$K_{\mu }(z)$, and can be thought of as a ‘modular’ or ‘theta’ relation wherein modified Bessel functions, instead of exponential functions, appear. Appearing in the second identity are 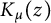$K_{\mu }(z)$, the Bessel functions of imaginary argument 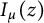$I_{\mu }(z)$, and ordinary hypergeometric functions 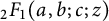${_2F_1}(a,b;c;z)$. Although certain special cases appear in the literature, the general identities are new. The arithmetical functions appearing in the identities include Ramanujan’s arithmetical function 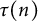$\tau (n)$, the number of representations of n as a sum of k squares 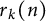$r_k(n)$, and primitive Dirichlet characters 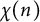$\chi (n)$.

Keywords

Bessel functionsfunctional equationsclassical arithmetic functions

MSC classification

Primary: 33C10: Bessel and Airy functions, cylinder functions, $_0F_1$
Secondary: 11M06: $zeta (s)$ and $L(s, chi)$ 11N99: None of the above, but in this section

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 6 , December 2023 , pp. 1800 - 1830
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first and second authors sincerely thank the MHRD SPARC project SPARC/2018-2019/P567/SL for their financial support. The first author is also supported by a grant from the Simons Foundation. The third author is a postdoctoral fellow at IIT Gandhinagar supported, in part, by the grant CRG/2020/002367.

References

Andrews, G. E., Askey, R. A., and Roy, R., Special functions, Cambridge University Press, Cambridge, 1999.10.1017/CBO9781107325937CrossRefGoogle Scholar
Andrews, G. E. and Berndt, B. C., Ramanujan’s lost notebook, part IV, Springer, New York, 2013.10.1007/978-1-4614-4081-9CrossRefGoogle Scholar
Berndt, B. C., Identities involving the coefficients of a class of Dirichlet series. III . Trans. Amer. Math. Soc. 146(1969), 323–348.CrossRefGoogle Scholar
Berndt, B. C., Identities involving the coefficients of a class of Dirichlet series. V . Trans. Amer. Math. Soc. 160(1971), 139–156.CrossRefGoogle Scholar
Berndt, B. C., Dixit, A., Gupta, R., and Zaharescu, A., A class of identities associated with Dirichlet series satisfying Hecke’s functional equation . Proc. Amer. Math. Soc. 150(2022), no. 11, 4785–4799.CrossRefGoogle Scholar
Berndt, B. C., Dixit, A., Kim, S., and Zaharescu, A., Sums of squares and products of Bessel functions . Adv. Math. 338(2018), 305–338.CrossRefGoogle Scholar
Berndt, B. C., Lee, Y., and Sohn, J., Koshliakov’s formula and Guinand’s formula in Ramanujan’s lost notebook . In: Alladi, K. (ed.), Surveys in number theory, Springer, New York, 2008, pp. 21–42.Google Scholar
Bochner, S., Some properties of modular relations . Ann. Math. 53(1951), 332–363.CrossRefGoogle Scholar
Chandrasekharan, K. and Narasimhan, R., Hecke’s functional equation and arithmetical identities . Ann. Math. 4(1961), 1–23.CrossRefGoogle Scholar
Cohen, H., A course in computational algebraic number theory, Springer, Berlin, 1993.10.1007/978-3-662-02945-9CrossRefGoogle Scholar
Davenport, H., Multiplicative number theory, 3rd. ed., Springer, New York, 2000.Google Scholar
Dixon, A. L. and Ferrar, W. L., Some summations over the lattice points of a circle (I) . Quart. J. Math. 5(1934), 48–63.10.1093/qmath/os-5.1.48CrossRefGoogle Scholar
Edwards, H. M., Riemann’s zeta function, Academic Press, New York, 1974.Google Scholar
Fock, V. A., Zur Berechnung des elektromagnetischen Wechselstromfeldes bei ebener Begrenzung . Ann. Phys. 17(1933), no. 5, 401–420.10.1002/andp.19334090405CrossRefGoogle Scholar
Fock, V. A. and Bursian, V., Electromagnetic field of alternating current in a circuit with two groundings , J. Russian Phys. Chem. Soc. 58(2) (1926), 355–363 (in Russian).Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series and products, 5th ed., Academic Press, San Diego, 1994.Google Scholar
Guinand, A. P., Some rapidly convergent series for the Riemann $\xi$ -function . Quart. J. Math. (Oxford) 6(1955), 156–160.CrossRefGoogle Scholar
Hardy, G. H., On the expression of a number as the sum of two squares , Quart. J. Pure Appl. Math. 46 (1915), 263–283.Google Scholar
Koshliakov, N. S., On some summation formulae connected with the theory of numbers. II . C. R. Acad. Sci. URSS 1(1934), 553–556 (in Russian).Google Scholar
Koshliakov, N. S., On a certain definite integral connected with the cylindric function ${\mathrm{J}}_{\unicode{x3bc}}(\mathrm{x})$ . C. R. Acad. Sci. URSS 2(1934), 145–147.Google Scholar
Maass, H., Über eine neue art von nichtanalytischen automorphen Funktionen and die Bestimmung Dirichletscher Reihen durch Funktionalgleichungen . Math. Ann. 121(1949), 141–183.CrossRefGoogle Scholar
Oberhettinger, F. and Soni, K., On some relations which are equivalent to functional equations involving the Riemann zeta function . Math. Z. 127(1972), 17–34.CrossRefGoogle Scholar
Prudnikov, A. P., Brychkov, Y. A., and Marichev, O. I., Integrals and series, vol. 3, Gordon and Breach, New York, 2003.Google Scholar
Ramanujan, S., The lost notebook and other unpublished papers, Narosa, New Delhi, 1988.Google Scholar
Watson, G. N., Some self-reciprocal functions . Quart. J. Math. (Oxford) 2(1931), 298–309.CrossRefGoogle Scholar
Watson, G. N., Theory of Bessel functions, 2nd ed., Cambridge University Press, London, 1966.Google Scholar