Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hambleton, Ian
and
Madsen, Ib
1986.
Local surgery obstructions and space forms.
Mathematische Zeitschrift,
Vol. 193,
Issue. 2,
p.
191.
Hambleton, I.
Ranicki, A.
and
Taylor, L.
1987.
Round L-theory.
Journal of Pure and Applied Algebra,
Vol. 47,
Issue. 2,
p.
131.
Davis, James F.
1988.
Evaluation of odd-dimensional surgery obstructions with finite fundamental group.
Topology,
Vol. 27,
Issue. 2,
p.
179.
Madsen, Ib
and
Rothenberg, Mel
1988.
On the homotopy theory of equivariant automorphism groups.
Inventiones Mathematicae,
Vol. 94,
Issue. 3,
p.
623.
Madsen, I.
and
Rothenberg, M.
1989.
Transformation Groups.
Vol. 1375,
Issue. ,
p.
216.
Hambleton, I.
Taylor, Laurence
and
Williams, Bruce
1990.
Detection theorems for K-theory and L-theory.
Journal of Pure and Applied Algebra,
Vol. 63,
Issue. 3,
p.
247.
Hambleton, Ian
and
Pedersen, Erik Kjær
1991.
Bounded surgery and dihedral group actions on spheres.
Journal of the American Mathematical Society,
Vol. 4,
Issue. 1,
p.
105.
Ferry, Steven C.
and
Pedersen, Erik Kjaer
1991.
Some mildly wild circles in Sn arising from algebraic K-Theory.
K-Theory,
Vol. 4,
Issue. 5,
p.
479.
Hillman, Jonathan A.
1993.
On 4-manifolds with universal covering space S2 × R2 or S3 × R.
Topology and its Applications,
Vol. 52,
Issue. 1,
p.
23.
Hambleton, Ian
and
Madsen, Ib
1993.
On the computation of the projective surgery obstruction groups.
K-Theory,
Vol. 7,
Issue. 6,
p.
537.
Williams, Bruce
2005.
Handbook of K-Theory.
p.
611.
Khan, Qayum
2009.
Reduction of UNil for finite groups with normal abelian Sylow 2-subgroup.
Journal of Pure and Applied Algebra,
Vol. 213,
Issue. 3,
p.
279.
Hillman, Jonathan A
2012.
Indecomposable PD3–complexes.
Algebraic & Geometric Topology,
Vol. 12,
Issue. 1,
p.
131.
Wall, C. T. C.
2013.
Lie Groups: Structure, Actions, and Representations.
Vol. 306,
Issue. ,
p.
381.
Bleile, Beatrice
Bokor, Imre
and
Hillman, Jonathan
2018.
Poincaré duality complexes with highly
connected universal cover.
Algebraic & Geometric Topology,
Vol. 18,
Issue. 7,
p.
3749.
Hillman, Jonathan
2020.
Poincaré Duality in Dimension 3.
Open Book Series,
Vol. 3,
Issue. 1,
p.
1.
Hillman, Jonathan
2020.
Poincaré Duality in Dimension 3.
Open Book Series,
Vol. 3,
Issue. 1,
p.
1.
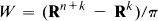
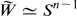 as considered by Swan [41].
as considered by Swan [41].
