No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
An  $E$-ring is a unital ring
$E$-ring is a unital ring 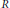 $R$ such that every endomorphism of the underlying abelian group
$R$ such that every endomorphism of the underlying abelian group 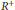 ${{R}^{+}}$ is multiplication by some ring element. The existence of almost-free
${{R}^{+}}$ is multiplication by some ring element. The existence of almost-free  $E$-rings of cardinality greater than
$E$-rings of cardinality greater than 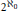 ${{2}^{{{\aleph }_{0}}}}$ is undecidable in ZFC. While they exist in Gödel's universe, they do not exist in other models of set theory. For a regular cardinal
${{2}^{{{\aleph }_{0}}}}$ is undecidable in ZFC. While they exist in Gödel's universe, they do not exist in other models of set theory. For a regular cardinal 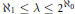 ${{\aleph }_{1}}\le \text{ }\!\!\lambda\!\!\text{ }\le {{2}^{{{\aleph }_{0}}}}$ we construct
${{\aleph }_{1}}\le \text{ }\!\!\lambda\!\!\text{ }\le {{2}^{{{\aleph }_{0}}}}$ we construct  $E$-rings of cardinality
$E$-rings of cardinality  $\lambda $ in ZFC which have
$\lambda $ in ZFC which have 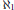 ${{\aleph }_{1}}$-free additive structure. For
${{\aleph }_{1}}$-free additive structure. For 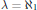 $\text{ }\!\!\lambda\!\!\text{ }={{\aleph }_{1}}$ we therefore obtain the existence of almost-free
$\text{ }\!\!\lambda\!\!\text{ }={{\aleph }_{1}}$ we therefore obtain the existence of almost-free  $E$-rings of cardinality
$E$-rings of cardinality 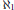 ${{\aleph }_{1}}$ in ZFC.
${{\aleph }_{1}}$ in ZFC.