No CrossRef data available.
Article contents
An Infinite Order Whittaker Function
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we construct a flat smooth section of an induced space 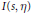 $I(s,\eta )$ of
$I(s,\eta )$ of 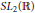 $S{{L}_{2}}\left( \mathbb{R} \right)$ so that the attached Whittaker function is not of finite order. An asymptotic method of classical analysis is used.
$S{{L}_{2}}\left( \mathbb{R} \right)$ so that the attached Whittaker function is not of finite order. An asymptotic method of classical analysis is used.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
de Bruijn, N. G., Asymptotic Methods in Analysis.
Dover Publications, New York, 1981.Google Scholar
[2]
Cogdell, J. W. and Piatetski-Shapiro, I. I., Converse theorems for GLn II.
J. Reine Angew. Math. 507(1999), 165–188.Google Scholar
[3]
Cohn, L., Analytic theory of the Harish–Chandra C-function.
Lecture Notes in Mathematics 429, Springer-Verlag, Berlin–New York, 1974.Google Scholar
[5]
Gelbart, S. and Shahidi, F., Boundedness of a Automorphic L-functions in vertical strips.
J. Amer. Math. Soc. 14(2001), no. 1, 79–107.Google Scholar
[6]
Jacquet, H., Fonctions de Whittaker associeés aux groupes de Chevalley.
Bull. Soc. Math. France
95(1967), 243–309.Google Scholar
[7]
Kim, H. H., Functoriality for the exterior square of GL 4 and the symmetric fourth of GL 2, J. Amer. Math. Soc. 16(2003), no. 1, 139–183.Google Scholar
[8]
Kim, H. H. and Shahidi, F., Functorial products for GL 2 × GL 3 and the symmetric cube for GL 2. Ann. of Math. 155(2002), no. 3, 837–893.Google Scholar
[9]
Langlands, R., Euler products.
Yale Mathematical Monographs 1, Yale University Press, New Haven, CT, 1971.Google Scholar
[10]
Langlands, R., On the functional equations satisfied by Eisenstein series.
Lecture Notes in Mathematics 544, Springer-Verlag, Berlin-New York, 1976.Google Scholar
[11]
Mc Kee, M., On the finite order of Whittaker functions, Eisenstein series, and automorphic L-functions. Ph. D. thesis, Princeton University, 2003.Google Scholar
[13]
Schiffman, G., Intégrales d';interlacement et fonctions de Whittaker.
Bull. Soc. Math. France
99(1971), 3–72.Google Scholar
[14]
Shahidi, F., Functional equation satisfied by certain L-functions.
Compositio Math. 37(1978), no. 2, 171–207.Google Scholar
[15]
Shahidi, F.,Whittaker models for real groups.
Duke Math. J. 47(1980), no. 1, 99–125.Google Scholar
[17]
Shahidi, F., Local coefficients as Artin factors for real groups.
Duke Math. J. 52(1985), no. 4, 973–1007.Google Scholar
[18]
Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions.
Ann. of Math. 127(1988), no. 3, 547–584.Google Scholar
[19]
Shahidi, F., A proof of Langlands’ conjecture on Plancherel measures; Complementary series for p-adic groups.
Ann. of Math
132(1990), no. 2, 273–330.Google Scholar
[20]
Shalika, J. A., The multiplicity one theorem for GLn.
Ann. of Math. 100(1974), 171–193.Google Scholar
[21]
Wallach, N. R., Real reductive groups I.
Pure and Applied Mathematics 132, Academic Press, Boston, MA, 1988.Google Scholar
[22]
Wallach, N. R., Real reductive groups II.
Pure and Applied Mathematics 132-II, Academic Press, Boston, MA, 1992.Google Scholar

