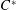Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matsumoto, Kengo
2021.
<inline-formula><tex-math id="M1">$ C^* $</tex-math></inline-formula>-algebras associated with asymptotic equivalence relations defined by hyperbolic toral automorphisms.
Electronic Research Archive,
Vol. 29,
Issue. 4,
p.
2645.
Matsumoto, Kengo
2021.
An étale equivalence relation on a tiling space arising from a two-sided subshift and associatedC*-algebras.
Dynamical Systems,
Vol. 36,
Issue. 3,
p.
445.
MATSUMOTO, KENGO
2022.
-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS.
Journal of the Australian Mathematical Society,
Vol. 112,
Issue. 2,
p.
230.
Qiang, Xiangqi
and
Hou, Chengjun
2024.
Continuous Orbit Equivalence for Automorphism Systems of Equivalence Relations.
Taiwanese Journal of Mathematics,
Vol. 28,
Issue. 1,
Qiang, Xiang Qi
and
Hou, Cheng Jun
2024.
Continuous Orbit Equivalence of Semigroup Actions.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 6,
p.
1581.