Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-21T17:59:44.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic Maximum Principles for Subharmonic and Plurisubharmonic Functions

Published online by Cambridge University Press:  20 November 2018

P. M. Gauthier ,
R. Grothmann  and
W. Hengartner
P. M. Gauthier
Affiliation:
Université de Montréal, Montréal, Québec
R. Grothmann
Affiliation:
Kath, Universitàt Eichstätt, Federal Republic of Germany
W. Hengartner
Affiliation:
Université Laval, Québec, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Ω be a bounded open set in Rn. An immediate consequence of the maximum principle is that if s is a function continuous on 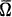and subharmonic on Ω, then

(1)

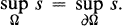
Of course (1) is no longer true if Ω is not bounded. For example in C ∼ R2 consider the functions

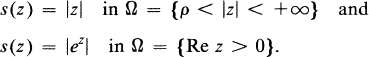
However, if we restrict the growth of s, then (1) may still hold even if the open set Ω is no longer bounded and such is the theme of Phragmèn-Lindelöf type theorems. If we assume even more, namely, that s is upper-bounded, then we can again infer (1) for unbounded open sets Ω. We shall return to this point later.

In the present note, we wish to prove (1) for an arbitrary subharmonic function s on an open subset Ω of Rn. In particular, we do not assume that s is bounded or even of restricted growth. Rather, we impose restrictions on the (possibly unbounded) set Ω.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 2 , 01 April 1988 , pp. 477 - 486
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bagby, T., A Runge theorem for harmonic functions on closed subsets of Riemann surfaces, Proc. Amer. Math. Soc. (accepted).CrossRefGoogle Scholar
2. Blanchet, P., Oral communication. Google Scholar
3. Boivin, A., Approximation uniforme harmonique et tangentielle holomorphe ou méromorphe sur les surfaces de Riemann, Ph.D. Thesis, Université de Montréal (1984.,Google Scholar
. Calabi, E., An intrinsic characterization of harmonie one-forms, In Global analysis (Univ. Tokyo Press, Tokyo, (1969), 101–117.Google Scholar
5. Gaidenko, S. V., Growth of harmonic functions near a boundary, Differential Equations 21 (1985), 557–561.Google Scholar
6. Gauthier, P. M., Goldstein, M. and Ow, W. H., Uniform approximation on closed sets by harmonic functions with Newtonian singularities, J. London Math. Soc. (2) 28 (1983), 71–82.Google Scholar
7. Gauthier, P. M., Hengartner, W. and Stray, A., A problem of Rube I concerning approximation on unbounded sets by entire functions, Rocky Mountain J. (accepted).Google Scholar
8. Sario, L. et al., Classification theory of Riemannian manifolds, S.L.N. 605 (Springer-Verlag, Berlin-Heidelberg-New York, 1977).CrossRefGoogle Scholar
9. Stray, A., Decomposition of approximable functions. Ann. Math. 720(1984), 225–235.Google Scholar