Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-09T02:13:54.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Bakry–Émery Curvature Functions on Graphs

Part of: Graph theory Discrete geometry Classical differential geometry

Published online by Cambridge University Press:  07 January 2019

David Cushing ,
Shiping Liu  and
Norbert Peyerimhoff
David Cushing
Affiliation:
Department of Mathematical Sciences, Durham University, Science Laboratories, South Road, Durham, DH1 3LE, United Kingdom e-mail: david.cushing@durham.ac.uknorbert.peyerimhoff@durham.ac.uk
Shiping Liu
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China e-mail: spliu@ustc.edu.cn
Norbert Peyerimhoff
Affiliation:
Department of Mathematical Sciences, Durham University, Science Laboratories, South Road, Durham, DH1 3LE, United Kingdom e-mail: david.cushing@durham.ac.uknorbert.peyerimhoff@durham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

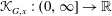We study local properties of the Bakry–Émery curvature function ${\mathcal{K}}_{G,x}:(0,\infty ]\rightarrow \mathbb{R}$ at a vertex $x$ of a graph 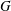$G$ systematically. Here 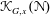${\mathcal{K}}_{G,x}({\mathcal{N}})$ is defined as the optimal curvature lower bound 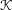${\mathcal{K}}$ in the Bakry–Émery curvature-dimension inequality 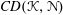$CD({\mathcal{K}},{\mathcal{N}})$ that $x$ satisfies. We provide upper and lower bounds for the curvature functions, introduce fundamental concepts like curvature sharpness and 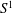$S^{1}$-out regularity, and relate the curvature functions of 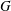$G$ with various spectral properties of (weighted) graphs constructed from local structures of 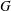$G$. We prove that the curvature functions of the Cartesian product of two graphs 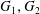$G_{1},G_{2}$ are equal to an abstract product of curvature functions of 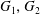$G_{1},G_{2}$. We explore the curvature functions of Cayley graphs and many particular (families of) examples. We present various conjectures and construct an infinite increasing family of 6-regular graphs which satisfy 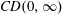$CD(0,\infty )$ but are not Cayley graphs.

Keywords

Bakry–Emery curvaturecurvature-dimension inequalityCayley graphCartesian product

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 52C99: None of the above, but in this section 53A40: Other special differential geometries
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 1 , February 2020 , pp. 89 - 143
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the EPSRC Grant EP/K016687/1 “Topology, Geometry and Laplacians of Simplicial Complexes”.

References

Alon, N. and Roichman, Y., Random Cayley graphs and expanders . Random Structures Algorithms 5(1994), no. 2, 271–284. https://doi.org/10.1002/rsa.3240050203.Google Scholar
Bakry, D., Functional inequalities for Markov semigroups. In: Probability measures on groups: recent directions and trends. Tata Inst. Fund. Res., Mumbai, 2006, pp. 91–147.Google Scholar
Bakry, D. and Émery, M., Diffusions hypercontractives . Lecture Notes in Math. 1123, Springer, Berlin, 1985, pp. 177–206.. https://doi.org/10.1007/BFb0075847.Google Scholar
Bauer, F., Horn, P., Lin, Y., Lippner, G., Mangoubi, D., and Yau, S.-T., Li-Yau inequality on graphs . J. Differential Geom. 99(2015), no. 3, 359–405.Google Scholar
Brouwer, A. E. and Haemers, W. H., Spectra of graphs . Universitext, Springer, New York, 2012. https://doi.org/10.1007/978-1-4614-1939-6.Google Scholar
Chung, F. R. K., Lin, Y., and Yau, S.-T., Harnack inequalities for graphs with non-negative Ricci curvature . J. Math. Anal. Appl. 415(2014), 25–32. https://doi.org/10.1016/j.jmaa.2014.01.044.Google Scholar
Chung, F. R. K. and Yau, S.-T., Logarithmic Harnack inequalities . Math. Res. Lett. 3(1996), no. 6, 793–812. https://doi.org/10.4310/MRL.1996.v3.n6.a8.Google Scholar
Cushing, D., Kangaslampi, R., Lipläinen, V., Liu, S., and Stagg, G. W., The graph curvature calculator and the curvatures of cubic graphs. arxiv:1712.03033.Google Scholar
Davis, M. W., The geometry and topology of Coxeter groups . London Mathematical Society Monographs Series, 32. Princeton University Press, Princeton, NJ, 2008.Google Scholar
Friedman, J., Murty, R., and Tillich, J.-P., Spectral estimates for abelian Cayley graphs . J. Combin. Theory Ser. B 96(2006), no. 1, 111–121. https://doi.org/10.1016/j.jctb.2005.06.012.Google Scholar
Godsil, C. and Royle, G., Algebraic graph theory . Graduate Texts in Mathematics, 207. Springer-Verlag, New York, 2001. https://doi.org/10.1007/978-1-4613-0163-9.Google Scholar
Horn, P., Lin, Y., Liu, Shuang, and Yau, S.-T., Volume doubling, Poincaré inequality and Gaussian heat kernel estimate for nonnegative curvature graphs. J. Reine Angew Math. https://doi.org/10.1515/crelle-2017-0038.Google Scholar
Hua, B. and Lin, Y., Stochastic completeness for graphs with curvature dimension conditions . Adv. Math. 306(2017), 279–302. https://doi.org/10.1016/j.aim.2016.10.022.Google Scholar
Hua, B. and Lin, Y., Graphs with large girth and nonnegative curvature dimension condition . Comm. Anal. Geom., to appear. arxiv:1608.07000.Google Scholar
Jost, J. and Liu, S., Ollivier’s Ricci curvature, local clustering and curvature-dimension inequalities on graphs . Discrete Comput. Geom. 51(2014), no. 2, 300–322. https://doi.org/10.1007/s00454-013-9558-1.Google Scholar
Klartag, B., Kozma, G., Ralli, P., and Tetali, P., Discrete curvature and abelian groups . Canad. J. Math. 68(2016), 655–674. https://doi.org/10.4153/CJM-2015-046-8.Google Scholar
Kolesnikov, A. V. and Milman, E., Brascamp–Lieb type inequalities on weighted Riemannian manifolds with boundary . J. Geom. Anal. 27(2017), no. 2, 1680–1702. https://doi.org/10.1007/s12220-016-9736-5.Google Scholar
Lakzian, A. and McGuirk, Z., A global Poincaré inequality on graphs via a conical curvature-dimension condition . Anal. Geom. Metr. Spaces 6(2018), 32–47. https://doi.org/10.1515/agms- 2018- 0002.Google Scholar
Lin, Y. and Yau, S.-T., Ricci curvature and eigenvalue estimate on locally nite graphs . Math. Res. Lett. 17(2010), no. 2, 343–356. https://doi.org/10.4310/MRL.2010.v17.n2.a13.Google Scholar
Liu, S., Münch, F., and Peyerimhoff, N., Curvature and higher order Buser inequalities for the graph connection Laplacian . SIAM J. Discrete Math., to appear. arxiv:1512.08134.Google Scholar
Liu, S., Münch, F., and Peyerimhoff, N., Bakry-Émery curvature and diameter bounds on graphs . Calc. Var. Partial Differential Equations 57(2018), 57–67. arxiv:1608.07778 https://doi.org/10.1007/s00526-018-1334-x.Google Scholar
Liu, S. and Peyerimhoff, N., Eigenvalue ratios of nonnegatively curved graphs . Combinatorics, Probability and Computing. https://doi.org/10.1017/s0963548318000214.Google Scholar
Münch, F., Li-Yau inequality on finite graphs via non-linear curvature dimension conditions. arxiv:1412.3340.Google Scholar
Münch, F., Remarks on curvature dimension conditions on graphs . Calc. Var. Partial Differential Equations 56(2017), no. 1. Art. 11, 8 pp. https://doi.org/10.1007/s00526-016-1104-6.Google Scholar
Ohta, S., (K, N)-convexity and the curvature-dimension condition for negative . N. J. Geom. Anal. 26(2016), no. 3, 2067–2096. https://doi.org/10.1007/s12220-015-9619-1.Google Scholar
Qian, Z., Estimates for weighted volumes and applications . Quart. J. Math. Oxford Ser. (2) 48(1997), no. 190, 235–242. https://doi.org/10.1093/qmath/48.2.235.Google Scholar
Schmuckenschläger, M., Curvature of nonlocal Markov generators. In: Convex geometric analysis. Math. Sci. Res. Inst. Publ., 34. Cambridge Univ. Press, Cambridge, 1999, pp. 189–197.Google Scholar