Article contents
The Batalin–Vilkovisky Algebra in the String Topology of Classifying Spaces
Published online by Cambridge University Press: 09 January 2019
Abstract
For almost any compact connected Lie group 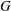 $G$ and any field
$G$ and any field 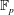 $\mathbb{F}_{p}$, we compute the Batalin–Vilkovisky algebra
$\mathbb{F}_{p}$, we compute the Batalin–Vilkovisky algebra 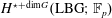 $H^{\star +\text{dim}\,G}(\text{LBG};\mathbb{F}_{p})$ on the loop cohomology of the classifying space introduced by Chataur and the second author. In particular, if
$H^{\star +\text{dim}\,G}(\text{LBG};\mathbb{F}_{p})$ on the loop cohomology of the classifying space introduced by Chataur and the second author. In particular, if 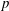 $p$ is odd or
$p$ is odd or 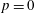 $p=0$, this Batalin–Vilkovisky algebra is isomorphic to the Hochschild cohomology
$p=0$, this Batalin–Vilkovisky algebra is isomorphic to the Hochschild cohomology 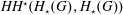 $HH^{\star }(H_{\star }(G),H_{\star }(G))$. Over
$HH^{\star }(H_{\star }(G),H_{\star }(G))$. Over 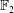 $\mathbb{F}_{2}$ , such an isomorphism of Batalin–Vilkovisky algebras does not hold when
$\mathbb{F}_{2}$ , such an isomorphism of Batalin–Vilkovisky algebras does not hold when 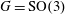 $G=\text{SO}(3)$ or
$G=\text{SO}(3)$ or 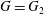 $G=G_{2}$. Our elaborate considerations on the signs in string topology of the classifying spaces give rise to a general theorem on graded homological conformal field theory.
$G=G_{2}$. Our elaborate considerations on the signs in string topology of the classifying spaces give rise to a general theorem on graded homological conformal field theory.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
The first author was partially supported by JSPS KAKENHI Grant Number 25287008.
References
- 1
- Cited by

