Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-08T15:45:51.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds for Lattice Polytopes Containing a Fixed Number of Interior Points in a Sublattice

Published online by Cambridge University Press:  20 November 2018

Jeffrey C. Lagarias  and
Günter M. Ziegler
Jeffrey C. Lagarias
Affiliation:
AT&T Bell Laboratories, Room 2C-373, Murray Hill, New Jersey, U.S.A. 07974
Günter M. Ziegler
Affiliation:
Universität Augsburg, Augsburg, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

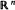A lattice polytope is a polytope in whose vertices are all in 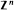. The volume of a lattice polytope P containing exactly k ≥ 1 points in d 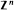in its interior is bounded above by 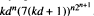. Any lattice polytope in 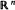of volume V can after an integral unimodular transformation be contained in a lattice cube having side length at most n˙n ! V. Thus the number of equivalence classes under integer unimodular transformations of lattice poly topes of bounded volume is finite. If S is any simplex of maximum volume inside a closed bounded convex body K in 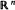having nonempty interior, then K⊆ ( n + 2)S — (n+ l)s where mS denotes a nomothetic copy of S with scale factor m, and s is the centroid of S.

Keywords

52A4311H0611P21
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 1022 - 1035
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Andrews, G.E., A lower bound for the volume of strictly convex bodies with many boundary lattice points, Trans. Amer. Math. Soc. 106 (1963), 270–279.Google Scholar
2. Blichfeldt, H., A new principle in the geometry of numbers, with some applications, Trans. Amer. Math. Soc. 15 (1914), 227–235.Google Scholar
3. Cassels, J.W.S., An introduction to the geometry of numbers. Grundlehren Series 99, Springer-Verlag, 1971.Google Scholar
4. Gruber, P.M. and Lekkerkerker, C.G., Geometry of numbers. 2nd éd., North-Holland, Amsterdam, 1987.Google Scholar
5. Hensley, D., Lattice vertex poly topes with interior lattice points, Pacific J. Math. 105 (1983), 183–191.Google Scholar
6. Mahler, K., The geometry of numbers. Duplicated lecture notes, University of Colorado, 1950.Google Scholar
7. Rado, R., Some covering theorems (I), Proc. London Math. Soc. 51 (1949), 232–264.Google Scholar
8. Reznick, B., Lattice point simplices, Discrete Math. 60 (1986), 219–242.Google Scholar
9. Scott, R.P., On convex lattice polygons, Bull. Austral. Math. Soc. 15 (1976), 395–399.Google Scholar
10. Zaks, J., Perles, A. and Wills, J.M., On lattice polytopes having interior lattice points, Elemente der Math.Google Scholar