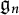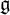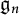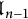1 Introduction
Truncated current Lie algebras have appeared in numerous parts of the literature in recent years, and a large part of their interest stems from the fact that they interpolate between the finite-dimensional simple Lie algebras and the vacuum parabolic of the corresponding untwisted affine Lie algebra. If
![]() $\mathfrak {g} = \operatorname {Lie}(G)$
is the Lie algebra of a complex reductive algebraic group, then the group
$\mathfrak {g} = \operatorname {Lie}(G)$
is the Lie algebra of a complex reductive algebraic group, then the group
![]() $G[t]$
of polynomial currents in G is the (infinite-dimensional) algebraic group of regular maps
$G[t]$
of polynomial currents in G is the (infinite-dimensional) algebraic group of regular maps
![]() $\mathbb {A}^1_{\mathbb {C}} \to G$
. The current Lie algebra
$\mathbb {A}^1_{\mathbb {C}} \to G$
. The current Lie algebra
![]() $\mathfrak {g}[t] := \operatorname {Lie} G[t] = \mathfrak {g} \otimes \mathbb {C}[t]$
is isomorphic to the derived subalgebra of a maximal parabolic of the Kac–Moody affinization of
$\mathfrak {g}[t] := \operatorname {Lie} G[t] = \mathfrak {g} \otimes \mathbb {C}[t]$
is isomorphic to the derived subalgebra of a maximal parabolic of the Kac–Moody affinization of
![]() $\mathfrak {g}$
, and the nth truncated current Lie algebra is the quotient
$\mathfrak {g}$
, and the nth truncated current Lie algebra is the quotient
![]() $\mathfrak {g}_n := \mathfrak {g} \otimes \mathbb {C}[t]/(t^{n+1})$
. Equivalently,
$\mathfrak {g}_n := \mathfrak {g} \otimes \mathbb {C}[t]/(t^{n+1})$
. Equivalently,
![]() $\mathfrak {g}_n$
can be described as the Lie algebra of the nth jet scheme
$\mathfrak {g}_n$
can be described as the Lie algebra of the nth jet scheme
![]() $J_n G$
of G.
$J_n G$
of G.
The first truncated currents Lie algebra
![]() $\mathfrak {g}_1$
appeared in the work of Takiff, and so they are often referred to as Takiff Lie algebras. He showed that the symmetric invariant algebra
$\mathfrak {g}_1$
appeared in the work of Takiff, and so they are often referred to as Takiff Lie algebras. He showed that the symmetric invariant algebra
![]() $S(\mathfrak {g}_1)^{\mathfrak {g}_1}$
is a polynomial algebra on
$S(\mathfrak {g}_1)^{\mathfrak {g}_1}$
is a polynomial algebra on
![]() $2\operatorname {rank}(\mathfrak {g})$
variables [Reference TakiffTa71], generalizing the classical theorem of Chevalley which describes
$2\operatorname {rank}(\mathfrak {g})$
variables [Reference TakiffTa71], generalizing the classical theorem of Chevalley which describes
![]() $S(\mathfrak {g}_0)^{\mathfrak {g}_0}$
. Later, Raïs and Tauvel extended Takiff’s theorem for arbitrary n [Reference Raïs and TauvelRT92]. Since the latter work is a crucial ingredient in our paper, we will briefly describe their main results in Section 2.2. More recently, Macedo and Savage extended their work further to the case of truncated multicurrents [Reference Macedo and SavageMS19], and Panyushev and Yakimova showed that for complex Lie algebras, the operation
$S(\mathfrak {g}_0)^{\mathfrak {g}_0}$
. Later, Raïs and Tauvel extended Takiff’s theorem for arbitrary n [Reference Raïs and TauvelRT92]. Since the latter work is a crucial ingredient in our paper, we will briefly describe their main results in Section 2.2. More recently, Macedo and Savage extended their work further to the case of truncated multicurrents [Reference Macedo and SavageMS19], and Panyushev and Yakimova showed that for complex Lie algebras, the operation
![]() $\mathfrak {g} \mapsto \mathfrak {g}_1$
preserves the property of having polynomial symmetric invariants, under mild assumptions [Reference Panyushev and YakimovaPY20].
$\mathfrak {g} \mapsto \mathfrak {g}_1$
preserves the property of having polynomial symmetric invariants, under mild assumptions [Reference Panyushev and YakimovaPY20].
These works on invariant theory have important applications in the theory of vertex algebras. Notably, the first approximation to describing the center of the critical-level universal affine vertex algebra associated with
![]() $\mathfrak {g}$
(a.k.a. the Feigin–Frenkel center) is the description of the semi-classical limit, which is equal to
$\mathfrak {g}$
(a.k.a. the Feigin–Frenkel center) is the description of the semi-classical limit, which is equal to
![]() $S(\mathfrak {g}[t^{-1}]t^{-1})^{\mathfrak {g}[t]}$
. This in turn can be described as the direct limit of the algebras
$S(\mathfrak {g}[t^{-1}]t^{-1})^{\mathfrak {g}[t]}$
. This in turn can be described as the direct limit of the algebras
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
discussed in the previous paragraph (see, for example, [Reference FrenkelFr07, Section 3.4] or [Reference MolevMo18, Section 6]). This connection with the Feigin–Frenkel center was recently used by Arakawa and Premet to provide a positive solution to Vinberg’s problem for centralizers, using affine W-algebras [Reference ArkhipovAP17]. We also mention the work of Kamgarpour [Reference KamgarpourKa16] for a discussion of the relationship with the geometric Langlands program. Another connection with the theory of W-algebras is given by the work of Brundan and Kleshchev [Reference Brundan and KleshchevBK06, Section 12], which states that the finite W-algebra for
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
discussed in the previous paragraph (see, for example, [Reference FrenkelFr07, Section 3.4] or [Reference MolevMo18, Section 6]). This connection with the Feigin–Frenkel center was recently used by Arakawa and Premet to provide a positive solution to Vinberg’s problem for centralizers, using affine W-algebras [Reference ArkhipovAP17]. We also mention the work of Kamgarpour [Reference KamgarpourKa16] for a discussion of the relationship with the geometric Langlands program. Another connection with the theory of W-algebras is given by the work of Brundan and Kleshchev [Reference Brundan and KleshchevBK06, Section 12], which states that the finite W-algebra for
![]() $\mathfrak {gl}_N$
associated with a nilpotent element with all Jordan blocks of size n is isomorphic to a truncated Yangian, which admits
$\mathfrak {gl}_N$
associated with a nilpotent element with all Jordan blocks of size n is isomorphic to a truncated Yangian, which admits
![]() $U(\mathfrak {g}_n)$
as a filtered degeneration.
$U(\mathfrak {g}_n)$
as a filtered degeneration.
This paper focuses on the representation theory of truncated current algebras. The most famous category of modules for a complex reductive Lie algebra
![]() $\mathfrak {g}$
is the Bernstein–Gelfand–Gelfand (BGG) category
$\mathfrak {g}$
is the Bernstein–Gelfand–Gelfand (BGG) category
![]() ${\mathcal {O}}$
, which is an abelian category containing all highest weight modules (see [Reference HumphreysHu08] for a survey). Wilson extended the notion of highest weight modules to all truncated currents [Reference WilsonWi11], and subsequently Mazorchuck and Sörderberg introduced a version of category
${\mathcal {O}}$
, which is an abelian category containing all highest weight modules (see [Reference HumphreysHu08] for a survey). Wilson extended the notion of highest weight modules to all truncated currents [Reference WilsonWi11], and subsequently Mazorchuck and Sörderberg introduced a version of category
![]() ${\mathcal {O}}$
for Takiff
${\mathcal {O}}$
for Takiff
![]() $\mathfrak {sl}_2$
[Reference Mazorchuk and SöderbergMSo19]. The most recent development in this field is the work of the first author [Reference ChaffeCh23], which made a thorough study of category
$\mathfrak {sl}_2$
[Reference Mazorchuk and SöderbergMSo19]. The most recent development in this field is the work of the first author [Reference ChaffeCh23], which made a thorough study of category
![]() ${\mathcal {O}}$
for all Takiff Lie algebras, eventually showing that the composition multiplicities of simple modules inside Verma modules can be determined by certain formulas involving Kazhdan–Lusztig polynomials. The results of the present paper generalize all of the main results of loc. cit. to the case of truncated current Lie algebras
${\mathcal {O}}$
for all Takiff Lie algebras, eventually showing that the composition multiplicities of simple modules inside Verma modules can be determined by certain formulas involving Kazhdan–Lusztig polynomials. The results of the present paper generalize all of the main results of loc. cit. to the case of truncated current Lie algebras
![]() $\mathfrak {g}_n$
.
$\mathfrak {g}_n$
.
For the rest of the introduction, we fix
![]() $\mathfrak {g} = \operatorname {Lie}(G)$
, where G is a complex reductive algebraic group, and fix
$\mathfrak {g} = \operatorname {Lie}(G)$
, where G is a complex reductive algebraic group, and fix
![]() $n> 0$
. We also fix a triangular decomposition
$n> 0$
. We also fix a triangular decomposition
![]() $\mathfrak {g} = \mathfrak {n}^- \oplus \mathfrak {h} \oplus \mathfrak {n}^+$
and write
$\mathfrak {g} = \mathfrak {n}^- \oplus \mathfrak {h} \oplus \mathfrak {n}^+$
and write
![]() $\mathfrak {b} = \mathfrak {h} \oplus \mathfrak {n}^+$
. This gives rise to a triangular decomposition
$\mathfrak {b} = \mathfrak {h} \oplus \mathfrak {n}^+$
. This gives rise to a triangular decomposition
![]() $\mathfrak {g}_n = \mathfrak {n}^-_n \oplus \mathfrak {h}_n \oplus \mathfrak {n}^+_n$
, and we say that a module is highest weight if it is generated (as a
$\mathfrak {g}_n = \mathfrak {n}^-_n \oplus \mathfrak {h}_n \oplus \mathfrak {n}^+_n$
, and we say that a module is highest weight if it is generated (as a
![]() $\mathfrak {g}_n$
-module) by a one-dimensional
$\mathfrak {g}_n$
-module) by a one-dimensional
![]() $\mathfrak {b}_n$
-module. These one-dimensional modules are parametrized by
$\mathfrak {b}_n$
-module. These one-dimensional modules are parametrized by
![]() $\mathfrak {h}_n^{*}$
, and the one-dimensional module afforded by
$\mathfrak {h}_n^{*}$
, and the one-dimensional module afforded by
![]() $\lambda \in \mathfrak {h}_n^{*}$
is denoted
$\lambda \in \mathfrak {h}_n^{*}$
is denoted
![]() $\mathbb {C}_\lambda $
. We define the universal highest weight module or Verma module of weight
$\mathbb {C}_\lambda $
. We define the universal highest weight module or Verma module of weight
![]() $\lambda $
by
$\lambda $
by
Since this is semisimple over
![]() $\mathfrak {h} = \mathfrak {h} \otimes 1 \subseteq \mathfrak {h}_n$
, with one-dimensional
$\mathfrak {h} = \mathfrak {h} \otimes 1 \subseteq \mathfrak {h}_n$
, with one-dimensional
![]() $\lambda |_{\mathfrak {h}}$
-weight space, it follows that it has a unique maximal submodule and a unique simple quotient, which we denote
$\lambda |_{\mathfrak {h}}$
-weight space, it follows that it has a unique maximal submodule and a unique simple quotient, which we denote
![]() $L_\lambda $
.
$L_\lambda $
.
We study the category
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
of finitely generated
${\mathcal {O}}(\mathfrak {g}_n)$
of finitely generated
![]() $\mathfrak {g}_n$
-modules on which
$\mathfrak {g}_n$
-modules on which
![]() $\mathfrak {n}_n^+$
acts locally nilpotently,
$\mathfrak {n}_n^+$
acts locally nilpotently,
![]() $\mathfrak {h}$
acts semisimply, and
$\mathfrak {h}$
acts semisimply, and
![]() $\mathfrak {h}_n^{\ge 1} := \mathfrak {h} \otimes t\mathbb {C}[t] / (t^{n+1}) \subseteq \mathfrak {h}_n$
acts locally finitely (see Definition 3.1). This category is closed under quotients and submodules, and the simple modules are precisely
$\mathfrak {h}_n^{\ge 1} := \mathfrak {h} \otimes t\mathbb {C}[t] / (t^{n+1}) \subseteq \mathfrak {h}_n$
acts locally finitely (see Definition 3.1). This category is closed under quotients and submodules, and the simple modules are precisely
![]() $\{L_\lambda \mid \lambda \in \mathfrak {h}_n^{*}\}$
.
$\{L_\lambda \mid \lambda \in \mathfrak {h}_n^{*}\}$
.
One especially nice feature of the BGG category
![]() ${\mathcal {O}}$
for
${\mathcal {O}}$
for
![]() $\mathfrak {g}$
it that it is Artinian; however, this fails for
$\mathfrak {g}$
it that it is Artinian; however, this fails for
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
. Therefore, we define composition multiplicities
${\mathcal {O}}(\mathfrak {g}_n)$
. Therefore, we define composition multiplicities
![]() $[M : L_\mu ]$
using formal characters: every module
$[M : L_\mu ]$
using formal characters: every module
![]() $M \in {\mathcal {O}}(\mathfrak {g}_n)$
has finite-dimensional
$M \in {\mathcal {O}}(\mathfrak {g}_n)$
has finite-dimensional
![]() $\mathfrak {h}$
-weight spaces and the formal character
$\mathfrak {h}$
-weight spaces and the formal character
![]() $\operatorname {ch} M$
can be expressed uniquely as a nonnegative integral linear combinations of characters of simple modules. We call the coefficients appearing in these sums the composition multiplicities of
$\operatorname {ch} M$
can be expressed uniquely as a nonnegative integral linear combinations of characters of simple modules. We call the coefficients appearing in these sums the composition multiplicities of
![]() $M \in {\mathcal {O}}(\mathfrak {g}_n)$
. We explain this in more detail in Section 6, and give a description (see Lemma 6.2) of the
$M \in {\mathcal {O}}(\mathfrak {g}_n)$
. We explain this in more detail in Section 6, and give a description (see Lemma 6.2) of the
![]() $[M : L_\lambda ]$
in the spirit of composition multiplicities for affine Lie algebras [Reference KacKac90, Proposition 9.7].
$[M : L_\lambda ]$
in the spirit of composition multiplicities for affine Lie algebras [Reference KacKac90, Proposition 9.7].
We now state the main result of this paper, which follows directly from Corollary 6.8.
Theorem 1.1 Let
![]() $n> 0$
, let G be a connected reductive group, and let
$n> 0$
, let G be a connected reductive group, and let
![]() $\lambda , \mu \in \mathfrak {h}_n^{*}$
. The composition multiplicity
$\lambda , \mu \in \mathfrak {h}_n^{*}$
. The composition multiplicity
![]() $[M_\lambda : L_\mu ]$
can be expressed via a precise formula (6.1) in terms of composition multiplicities of simple modules inside Verma modules for a truncated current algebra
$[M_\lambda : L_\mu ]$
can be expressed via a precise formula (6.1) in terms of composition multiplicities of simple modules inside Verma modules for a truncated current algebra
![]() ${\mathfrak {l}}_{n-1}$
where
${\mathfrak {l}}_{n-1}$
where
![]() ${\mathfrak {l}} = \operatorname {Lie}(L)$
for some Levi subgroup
${\mathfrak {l}} = \operatorname {Lie}(L)$
for some Levi subgroup
![]() $L \subseteq G$
.
$L \subseteq G$
.
Theorem 1.1 suggests an inductive procedure for calculating the composition multiplicities
![]() $[M_\lambda : L_\mu ]$
for the nth truncated current algebra in terms of the analogous composition multiplicities for
$[M_\lambda : L_\mu ]$
for the nth truncated current algebra in terms of the analogous composition multiplicities for
![]() $\mathfrak {g}_0$
. By the proof of the Kazhdan–Lusztig conjecture by Beilinson–Bernstein and Brylinski–Kashiwara (see [Reference Hotta, Takeuchi and TanisakiHTT08]), we know that for
$\mathfrak {g}_0$
. By the proof of the Kazhdan–Lusztig conjecture by Beilinson–Bernstein and Brylinski–Kashiwara (see [Reference Hotta, Takeuchi and TanisakiHTT08]), we know that for
![]() $n = 0$
, the composition multiplicities
$n = 0$
, the composition multiplicities
![]() $[M_\lambda : L_\mu ]$
are given by the evaluation at 1 of certain Kazhdan–Lusztig polynomials. Hence, for
$[M_\lambda : L_\mu ]$
are given by the evaluation at 1 of certain Kazhdan–Lusztig polynomials. Hence, for
![]() $n> 0$
, the values
$n> 0$
, the values
![]() $[M_\lambda : L_\mu ]$
can be described by formulas involving nonnegative integral linear combinations of these Kazhdan–Lusztig polynomials at 1. It is interesting to wonder whether our formulas have a natural geometric interpretation on the flag variety.
$[M_\lambda : L_\mu ]$
can be described by formulas involving nonnegative integral linear combinations of these Kazhdan–Lusztig polynomials at 1. It is interesting to wonder whether our formulas have a natural geometric interpretation on the flag variety.
We remark that the methods of this paper generalize those of [Reference ChaffeCh23]. In the rest of the introduction, we highlight some of our other key results, and describe the structure of the paper.
In Section 2, we introduce the basic notation, which will be used throughout the paper. We then recall the work of Raïs and Tauvel [Reference Raïs and TauvelRT92] on
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
and use it to describe the generators of the center of the enveloping algebra
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
and use it to describe the generators of the center of the enveloping algebra
![]() $U(\mathfrak {g}_n)$
.
$U(\mathfrak {g}_n)$
.
In Section 3, we describe all of the elementary properties of our category
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
. We also explain that the category can be decomposed into a direct sum of abelian subcategories which are parameterized by the generalized eigenspaces of
${\mathcal {O}}(\mathfrak {g}_n)$
. We also explain that the category can be decomposed into a direct sum of abelian subcategories which are parameterized by the generalized eigenspaces of
![]() $\mathfrak {h}\otimes t^i$
for
$\mathfrak {h}\otimes t^i$
for
![]() $i =1,...,n$
. The generalized eigenvalues are parametrized by
$i =1,...,n$
. The generalized eigenvalues are parametrized by
![]() $(\mathfrak {h}_n^{\ge 1})^{*}$
, and for
$(\mathfrak {h}_n^{\ge 1})^{*}$
, and for
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, we call the subcategory
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, we call the subcategory
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
a Jordan block of
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
a Jordan block of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
.
${\mathcal {O}}(\mathfrak {g}_n)$
.
In Section 4, we introduce one of our main tools for simplifying the study of Jordan blocks of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
. Let
${\mathcal {O}}(\mathfrak {g}_n)$
. Let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, and let
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, and let
![]() $\mu _n := \mu |_{\mathfrak {h}\otimes t^n}$
, which we identify with an element of
$\mu _n := \mu |_{\mathfrak {h}\otimes t^n}$
, which we identify with an element of
![]() $\mathfrak {h}^{*}$
in the obvious fashion. The centralizer
$\mathfrak {h}^{*}$
in the obvious fashion. The centralizer
![]() ${\mathfrak {l}} := \mathfrak {g}^{\mu _n}$
is a Levi subalgebra containing
${\mathfrak {l}} := \mathfrak {g}^{\mu _n}$
is a Levi subalgebra containing
![]() $\mathfrak {h}$
, and we suppose that it is the Levi factor of a standard parabolic
$\mathfrak {h}$
, and we suppose that it is the Levi factor of a standard parabolic
![]() $\mathfrak {p}\subseteq \mathfrak {g}$
such that
$\mathfrak {p}\subseteq \mathfrak {g}$
such that
![]() ${\mathfrak {r}} = \operatorname {Rad}(\mathfrak {p}) \subseteq \mathfrak {n}^+$
. In this case, we can parabolically induce modules from
${\mathfrak {r}} = \operatorname {Rad}(\mathfrak {p}) \subseteq \mathfrak {n}^+$
. In this case, we can parabolically induce modules from
![]() ${\mathcal {O}}^{(\mu )}({\mathfrak {l}}_n)$
to
${\mathcal {O}}^{(\mu )}({\mathfrak {l}}_n)$
to
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
. Similarly, we have a functor of
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
. Similarly, we have a functor of
![]() ${\mathfrak {r}}_n$
-invariants in the opposite direction.
${\mathfrak {r}}_n$
-invariants in the opposite direction.
A precise statement of the following result is given in Theorem 4.1.
Theorem 1.2 If
![]() ${\mathfrak {l}} = \mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, parabolic induction and
${\mathfrak {l}} = \mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, parabolic induction and
![]() ${\mathfrak {r}}_n$
-invariants are quasi-inverse equivalences between
${\mathfrak {r}}_n$
-invariants are quasi-inverse equivalences between
![]() ${\mathcal {O}}^{(\mu )}({\mathfrak {l}}_n)$
and
${\mathcal {O}}^{(\mu )}({\mathfrak {l}}_n)$
and
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
.
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
.
In the case where
![]() $\mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, the theorem allows us to reduce the study of
$\mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, the theorem allows us to reduce the study of
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
![]() $\mu _n$
is supported on the center of
$\mu _n$
is supported on the center of
![]() $\mathfrak {g}$
. Another simple reduction (Lemma 3.7) impels us to focus on the case
$\mathfrak {g}$
. Another simple reduction (Lemma 3.7) impels us to focus on the case
![]() $\mu _n = 0$
.
$\mu _n = 0$
.
Theorem 1.2 was inspired by a result of Friedlander and Parshall in modular representation theory of Lie algebras [Reference Friedlander and ParshallFP88, Theorem 3.2]. Using the fact that modules in
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
admit finite filtrations with highest weight sections (Lemma 3.3), the proof quickly reduces to showing that
${\mathcal {O}}(\mathfrak {g}_n)$
admit finite filtrations with highest weight sections (Lemma 3.3), the proof quickly reduces to showing that
![]() $(\bullet)^{{\mathfrak {r}}_n}$
is exact. This is the hardest part of the proof, and requires a careful study of central characters of highest weight modules (Theorem 4.2), which ultimately depends on our description of the center of
$(\bullet)^{{\mathfrak {r}}_n}$
is exact. This is the hardest part of the proof, and requires a careful study of central characters of highest weight modules (Theorem 4.2), which ultimately depends on our description of the center of
![]() $U(\mathfrak {g}_n)$
given in Section 2.2. In particular, in comparison to the Takiff case treated in [Reference ChaffeCh23, Section 4], the description of the central elements given by [Reference Raïs and TauvelRT92] is more difficult to work with.
$U(\mathfrak {g}_n)$
given in Section 2.2. In particular, in comparison to the Takiff case treated in [Reference ChaffeCh23, Section 4], the description of the central elements given by [Reference Raïs and TauvelRT92] is more difficult to work with.
In Section 5, we remove the requirement in Theorem 1.2 that
![]() ${\mathfrak {l}}$
is a standard Levi subalgebra; this is achieved with the use of twisting functors. These were first introduced by Arkhipov [Reference Arakawa and PremetAr01] and were applied to category
${\mathfrak {l}}$
is a standard Levi subalgebra; this is achieved with the use of twisting functors. These were first introduced by Arkhipov [Reference Arakawa and PremetAr01] and were applied to category
![]() ${\mathcal {O}}$
for
${\mathcal {O}}$
for
![]() $\mathfrak {g}$
by Andersen and Stroppel [Reference Andersen and StroppelAS03]. They were used in the context of Takiff Lie algebras by the first author in [Reference ChaffeCh23] while proving a similar reduction to that of the present paper. The main result of Section 5 is Theorem 5.9, which implies, together with Proposition 6.7, the following.
$\mathfrak {g}$
by Andersen and Stroppel [Reference Andersen and StroppelAS03]. They were used in the context of Takiff Lie algebras by the first author in [Reference ChaffeCh23] while proving a similar reduction to that of the present paper. The main result of Section 5 is Theorem 5.9, which implies, together with Proposition 6.7, the following.
Theorem 1.3 Every Jordan block of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
is equivalent to a Jordan block
${\mathcal {O}}(\mathfrak {g}_n)$
is equivalent to a Jordan block
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
such that
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
such that
![]() $\mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra.
$\mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra.
Together with Theorem 1.2, this allows us to reduce the study of Jordan blocks
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
![]() $\mu _n = 0$
. The proof of Theorem 1.3 is similar to [Reference ChaffeCh23, Theorem 5.7]; however, several of the proofs, especially the proofs of Lemmas 5.15 and 5.16, are significantly more complicated. As such, we provide detailed arguments for all of the proofs which are different, and refer the reader to the appropriate part of op. cit. otherwise.
$\mu _n = 0$
. The proof of Theorem 1.3 is similar to [Reference ChaffeCh23, Theorem 5.7]; however, several of the proofs, especially the proofs of Lemmas 5.15 and 5.16, are significantly more complicated. As such, we provide detailed arguments for all of the proofs which are different, and refer the reader to the appropriate part of op. cit. otherwise.
In Section 6, we address the problem of defining composition multiplicities and computing multiplicities of simples in Vermas. We begin by explaining how these numbers are defined and interpreting them in terms of composition series, which is all very similar to [Reference ChaffeCh23, Section 6.1], except that the structure of the filtrations considered in Lemma 6.2 is more complicated than the analogous filtrations in the Takiff case. Finally, we focus on the blocks
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
with
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
with
![]() $\mu _n = 0$
. The main result of the section is Corollary 6.8, which is a precise version of Theorem 1.1.
$\mu _n = 0$
. The main result of the section is Corollary 6.8, which is a precise version of Theorem 1.1.
2 Preliminaries
In this paper, all vector spaces, algebras, and algebraic varieties will be defined over
![]() $\mathbb {C}$
. Unadorned tensor products are taken over
$\mathbb {C}$
. Unadorned tensor products are taken over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
2.1 Reductive Lie algebras and truncated currents
From henceforth, we fix a reductive algebraic group G of rank r, with Lie algebra
![]() $\mathfrak {g}$
, and a choice of maximal torus
$\mathfrak {g}$
, and a choice of maximal torus
![]() $\mathfrak {h} \subseteq \mathfrak {g}$
. The Weyl group
$\mathfrak {h} \subseteq \mathfrak {g}$
. The Weyl group
![]() $N_G(\mathfrak {h}) / C_G(\mathfrak {h})$
will be denoted W. Let
$N_G(\mathfrak {h}) / C_G(\mathfrak {h})$
will be denoted W. Let
![]() $\Phi \subseteq \mathfrak {h}^{*}$
be the root system of
$\Phi \subseteq \mathfrak {h}^{*}$
be the root system of
![]() $\mathfrak {g}$
, and let
$\mathfrak {g}$
, and let
![]() $\Delta $
be a choice of simple roots for
$\Delta $
be a choice of simple roots for
![]() $\Phi $
, which give a set of positive roots
$\Phi $
, which give a set of positive roots
![]() $\Phi ^+ = \Phi \cap \sum _{\alpha \in \Delta } \mathbb {Z}_{\ge 0} \alpha $
. For each root
$\Phi ^+ = \Phi \cap \sum _{\alpha \in \Delta } \mathbb {Z}_{\ge 0} \alpha $
. For each root
![]() $\alpha \in \Phi $
, we have a one-dimensional root space
$\alpha \in \Phi $
, we have a one-dimensional root space
![]() $\mathfrak {g}_{\alpha }$
, and for positive roots
$\mathfrak {g}_{\alpha }$
, and for positive roots
![]() $\alpha $
, we fix a choice of triple
$\alpha $
, we fix a choice of triple
![]() $(e_{\alpha }, h_{\alpha }, f_{\alpha })$
such that
$(e_{\alpha }, h_{\alpha }, f_{\alpha })$
such that
![]() $e_{\alpha } \in \mathfrak {g}_{\alpha }$
,
$e_{\alpha } \in \mathfrak {g}_{\alpha }$
,
![]() $f_{\alpha } \in \mathfrak {g}_{-\alpha }$
, and
$f_{\alpha } \in \mathfrak {g}_{-\alpha }$
, and
![]() $h_{\alpha } := [e_{\alpha }, f_{\alpha }]$
, satisfying
$h_{\alpha } := [e_{\alpha }, f_{\alpha }]$
, satisfying
![]() $\alpha (h_{\alpha }) = 2$
.
$\alpha (h_{\alpha }) = 2$
.
These data give us a triangular decomposition
where
![]() $\mathfrak {n}^\pm := \bigoplus _{\alpha \in \Phi ^+} \mathfrak {g}_{\pm \alpha }$
. We also write
$\mathfrak {n}^\pm := \bigoplus _{\alpha \in \Phi ^+} \mathfrak {g}_{\pm \alpha }$
. We also write
![]() $\mathfrak {b} = \mathfrak {h} \oplus \mathfrak {n}^+$
for the corresponding Borel subalgebra of
$\mathfrak {b} = \mathfrak {h} \oplus \mathfrak {n}^+$
for the corresponding Borel subalgebra of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
For
![]() $n \geq 1$
, we consider the truncated current algebra
$n \geq 1$
, we consider the truncated current algebra
![]() $\mathfrak {g}_n := \mathfrak {g} \otimes \mathbb {C}[t]/(t^{n+1})$
. For any subalgebra
$\mathfrak {g}_n := \mathfrak {g} \otimes \mathbb {C}[t]/(t^{n+1})$
. For any subalgebra
![]() $\mathfrak {s} \subseteq \mathfrak {g}$
, we have a natural embedding
$\mathfrak {s} \subseteq \mathfrak {g}$
, we have a natural embedding
![]() $\mathfrak {s}_n \subseteq \mathfrak {g}_n$
of truncated currents. We make the notation
$\mathfrak {s}_n \subseteq \mathfrak {g}_n$
of truncated currents. We make the notation
![]() $\mathfrak {s}_n^i := \mathfrak {s}\otimes t^i \subseteq \mathfrak {g}_n$
. This gives a grading
$\mathfrak {s}_n^i := \mathfrak {s}\otimes t^i \subseteq \mathfrak {g}_n$
. This gives a grading
![]() $\mathfrak {s}_n = \bigoplus _{i=0}^n \mathfrak {s}_n^i$
. We write
$\mathfrak {s}_n = \bigoplus _{i=0}^n \mathfrak {s}_n^i$
. We write
![]() $\mathfrak {s}_n^{\ge m}$
for the sum of the graded pieces of degree
$\mathfrak {s}_n^{\ge m}$
for the sum of the graded pieces of degree
![]() $m,m+1,...,n$
.
$m,m+1,...,n$
.
For
![]() $x \in \mathfrak {g}$
and
$x \in \mathfrak {g}$
and
![]() $\alpha \in \Phi ^+$
, then we make the notation
$\alpha \in \Phi ^+$
, then we make the notation
 $$ \begin{align} \begin{array}{rcl} x_i &:=& x \otimes t^i, \\ e_{\alpha, i} &:=& e_{\alpha} \otimes t^i,\\ f_{\alpha, i} &:=& f_{\alpha} \otimes t^i,\\ h_{\alpha, i}&:=& h_{\alpha} \otimes t^i. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcl} x_i &:=& x \otimes t^i, \\ e_{\alpha, i} &:=& e_{\alpha} \otimes t^i,\\ f_{\alpha, i} &:=& f_{\alpha} \otimes t^i,\\ h_{\alpha, i}&:=& h_{\alpha} \otimes t^i. \end{array} \end{align} $$
We will often need to consider linear functions of
![]() $\mathfrak {g}_n$
and
$\mathfrak {g}_n$
and
![]() $\mathfrak {h}_n$
. If
$\mathfrak {h}_n$
. If
![]() $\lambda \in \mathfrak {h}_n^{*}$
, then we write
$\lambda \in \mathfrak {h}_n^{*}$
, then we write
 $$ \begin{align} \begin{array}{rcl} \lambda_i & :=& \lambda|_{\mathfrak{h}_n^i}, \\ \lambda_{\ge i} &:=& \lambda|_{\mathfrak{h}_n^{\ge i}}, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcl} \lambda_i & :=& \lambda|_{\mathfrak{h}_n^i}, \\ \lambda_{\ge i} &:=& \lambda|_{\mathfrak{h}_n^{\ge i}}, \end{array} \end{align} $$
for
![]() $i=0,...,n$
, and we often view
$i=0,...,n$
, and we often view
![]() $\lambda _i$
as an element of
$\lambda _i$
as an element of
![]() $\mathfrak {h}^{*}$
via the obvious identification
$\mathfrak {h}^{*}$
via the obvious identification
![]() $\mathfrak {h} = \mathfrak {h}_n^i$
. If
$\mathfrak {h} = \mathfrak {h}_n^i$
. If
![]() $\lambda \in \mathfrak {h}_n^{*}$
, then we can also view it as an element of
$\lambda \in \mathfrak {h}_n^{*}$
, then we can also view it as an element of
![]() $\mathfrak {g}_n^{*}$
by setting
$\mathfrak {g}_n^{*}$
by setting
![]() $\lambda (\mathfrak {n}_n^{\pm }) = 0$
.
$\lambda (\mathfrak {n}_n^{\pm }) = 0$
.
2.2 The symmetric invariants and the center of the enveloping algebra
We write
![]() $S(\mathfrak {g}_n)$
and
$S(\mathfrak {g}_n)$
and
![]() $U(\mathfrak {g}_n)$
for the symmetric algebra and the universal enveloping algebra of
$U(\mathfrak {g}_n)$
for the symmetric algebra and the universal enveloping algebra of
![]() $\mathfrak {g}_n$
, respectively. The algebra
$\mathfrak {g}_n$
, respectively. The algebra
![]() $U(\mathfrak {g}_n)$
is equipped with the PBW filtration, and the associated graded algebra is
$U(\mathfrak {g}_n)$
is equipped with the PBW filtration, and the associated graded algebra is
![]() $\operatorname {gr} U(\mathfrak {g}_n) = S(\mathfrak {g}_n)$
, the symmetric algebra on
$\operatorname {gr} U(\mathfrak {g}_n) = S(\mathfrak {g}_n)$
, the symmetric algebra on
![]() $\mathfrak {g}_n$
. In the present section, we describe the center
$\mathfrak {g}_n$
. In the present section, we describe the center
![]() $Z(\mathfrak {g}_n)$
of the enveloping algebra and its semi-classical limit.
$Z(\mathfrak {g}_n)$
of the enveloping algebra and its semi-classical limit.
The adjoint representation of
![]() $\mathfrak {g}_n$
extends uniquely to an action of
$\mathfrak {g}_n$
extends uniquely to an action of
![]() $\mathfrak {g}_n$
on both
$\mathfrak {g}_n$
on both
![]() $S(\mathfrak {g}_n)$
and
$S(\mathfrak {g}_n)$
and
![]() $U(\mathfrak {g}_n)$
by derivations [Reference DixmierDi77, Proposition 2.4.9]. The center
$U(\mathfrak {g}_n)$
by derivations [Reference DixmierDi77, Proposition 2.4.9]. The center
![]() $Z(\mathfrak {g}_n)$
is equal to
$Z(\mathfrak {g}_n)$
is equal to
![]() $U(\mathfrak {g}_n)^{\mathfrak {g}_n}$
, and the identification
$U(\mathfrak {g}_n)^{\mathfrak {g}_n}$
, and the identification
![]() $\operatorname {gr} U(\mathfrak {g}_n) = S(\mathfrak {g}_n)$
is
$\operatorname {gr} U(\mathfrak {g}_n) = S(\mathfrak {g}_n)$
is
![]() $\mathfrak {g}_n$
-equivariant. The invariant algebra
$\mathfrak {g}_n$
-equivariant. The invariant algebra
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
was first described by Raïs and Tauvel [Reference Raïs and TauvelRT92], as we now recall.
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
was first described by Raïs and Tauvel [Reference Raïs and TauvelRT92], as we now recall.
We define a series of (vector space) endomorphisms
![]() $\partial ^{(0)},..., \partial ^{(n)}$
of
$\partial ^{(0)},..., \partial ^{(n)}$
of
![]() $S(\mathfrak {g}_n)$
by putting
$S(\mathfrak {g}_n)$
by putting
![]() $\partial ^{(0)}$
equal to the identity map, and then inductively defining
$\partial ^{(0)}$
equal to the identity map, and then inductively defining
 $$ \begin{align} & \partial^{(k)}(x_j) = \left\{\begin{array}{cl} \binom{j}{k} x_{j-k}, & \text{ if } j \ge k,\\ 0, & \text{ otherwise}, \end{array} \right. \end{align} $$
$$ \begin{align} & \partial^{(k)}(x_j) = \left\{\begin{array}{cl} \binom{j}{k} x_{j-k}, & \text{ if } j \ge k,\\ 0, & \text{ otherwise}, \end{array} \right. \end{align} $$
for
![]() $x \in \mathfrak {g}$
and
$x \in \mathfrak {g}$
and
![]() $f,g \in S(\mathfrak {g}_n)$
. These endomorphisms will be used to construct the basic invariant generators introduced in op. cit. We remark that the family of operators
$f,g \in S(\mathfrak {g}_n)$
. These endomorphisms will be used to construct the basic invariant generators introduced in op. cit. We remark that the family of operators
![]() $(\partial ^{(0)},...,\partial ^{(n)})$
which we define here are an instance of higher order derivation [Reference Schmid and HasseSH], but we shall not use this formalism.
$(\partial ^{(0)},...,\partial ^{(n)})$
which we define here are an instance of higher order derivation [Reference Schmid and HasseSH], but we shall not use this formalism.
Recall Chevalley’s restriction theorem, which states that
![]() $S(\mathfrak {g})^G = S(\mathfrak {g})^{\mathfrak {g}} \cong S(\mathfrak {h})^W$
. Furthermore, the Chevalley–Sheppard–Todd theorem implies that
$S(\mathfrak {g})^G = S(\mathfrak {g})^{\mathfrak {g}} \cong S(\mathfrak {h})^W$
. Furthermore, the Chevalley–Sheppard–Todd theorem implies that
![]() $S(\mathfrak {g})^{\mathfrak {g}}$
is a graded polynomial algebra generated by
$S(\mathfrak {g})^{\mathfrak {g}}$
is a graded polynomial algebra generated by
![]() $\operatorname {rank}(\mathfrak {g})$
homogeneous elements. Write
$\operatorname {rank}(\mathfrak {g})$
homogeneous elements. Write
![]() $p_1,...,p_r$
for a choice of such elements.
$p_1,...,p_r$
for a choice of such elements.
The adjoint representation of
![]() $\mathfrak {g}_n$
stabilizes
$\mathfrak {g}_n$
stabilizes
![]() $\mathfrak {g}_n^n$
, and the action factors through the map
$\mathfrak {g}_n^n$
, and the action factors through the map
![]() $\mathfrak {g}_n \twoheadrightarrow \mathfrak {g}_n / \mathfrak {g}_n^{\ge 1} = \mathfrak {g}_0 = \mathfrak {g}$
. Therefore, we have a natural inclusion
$\mathfrak {g}_n \twoheadrightarrow \mathfrak {g}_n / \mathfrak {g}_n^{\ge 1} = \mathfrak {g}_0 = \mathfrak {g}$
. Therefore, we have a natural inclusion
![]() $S(\mathfrak {g})^{\mathfrak {g}} \hookrightarrow S(\mathfrak {g}_n^n)^{\mathfrak {g}_n}$
. Abusing notation, we view
$S(\mathfrak {g})^{\mathfrak {g}} \hookrightarrow S(\mathfrak {g}_n^n)^{\mathfrak {g}_n}$
. Abusing notation, we view
![]() $p_1,...,p_r$
as elements of
$p_1,...,p_r$
as elements of
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
.
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
.
Theorem 2.1 [Reference Raïs and TauvelRT92, Section 3]
The invariant algebra
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
is a polynomial ring generated by
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
is a polynomial ring generated by
![]() $(n+1)r$
elements
$(n+1)r$
elements
Let
![]() $d^{(k)} : S(\mathfrak {g}_n^n) \to S(\mathfrak {g}_n)$
be the partial derivative
$d^{(k)} : S(\mathfrak {g}_n^n) \to S(\mathfrak {g}_n)$
be the partial derivative
![]() $\sum _x x_{n-k} \frac {d}{dx_n}$
, where the sum is taken over a basis for
$\sum _x x_{n-k} \frac {d}{dx_n}$
, where the sum is taken over a basis for
![]() $\mathfrak {g}$
. Then it follows straight from the definitions (2.4) and (2.5) that there exist elements
$\mathfrak {g}$
. Then it follows straight from the definitions (2.4) and (2.5) that there exist elements
![]() $q_j^{(k)} \in S(\mathfrak {g}_n^{\ge n-k+1})$
such that
$q_j^{(k)} \in S(\mathfrak {g}_n^{\ge n-k+1})$
such that
We refer the reader to [Reference Raïs and TauvelRT92, Lemma 3.2(ii)] for the proof of (2.7). The next observation follows directly from the definitions, and we record it as a lemma for later use.
Lemma 2.2 The map
![]() $d^{(k)}$
sends
$d^{(k)}$
sends
![]() $\operatorname {ad}(\mathfrak {h})$
-invariants to
$\operatorname {ad}(\mathfrak {h})$
-invariants to
![]() $\operatorname {ad}(\mathfrak {h})$
-invariants.
$\operatorname {ad}(\mathfrak {h})$
-invariants.
Finally, we give a description of the center
![]() $Z(\mathfrak {g}_n)$
of the enveloping algebra. There is an isomorphism of
$Z(\mathfrak {g}_n)$
of the enveloping algebra. There is an isomorphism of
![]() $\mathfrak {g}_n$
-modules
$\mathfrak {g}_n$
-modules
![]() $\omega : S(\mathfrak {g}_n) \to U(\mathfrak {g}_n)$
called the symmetrization map [Reference DixmierDi77, Section 2.4]. It is defined by the rule
$\omega : S(\mathfrak {g}_n) \to U(\mathfrak {g}_n)$
called the symmetrization map [Reference DixmierDi77, Section 2.4]. It is defined by the rule
where
![]() $x^1,...,x^m \in \mathfrak {g}_n$
are any elements, so that
$x^1,...,x^m \in \mathfrak {g}_n$
are any elements, so that
![]() $x^1\cdots x^m \in S(\mathfrak {g}_n)$
is a monomial of degree m, and
$x^1\cdots x^m \in S(\mathfrak {g}_n)$
is a monomial of degree m, and
![]() $\mathfrak {S}_m$
denotes the symmetric group on m letters. If
$\mathfrak {S}_m$
denotes the symmetric group on m letters. If
![]() $\operatorname {gr} : U(\mathfrak {g}_n) \to S(\mathfrak {g}_n)$
is the (nonlinear) map defined by taking the top degree component with respect to the PBW filtration, then
$\operatorname {gr} : U(\mathfrak {g}_n) \to S(\mathfrak {g}_n)$
is the (nonlinear) map defined by taking the top degree component with respect to the PBW filtration, then
Since the isomorphism
![]() $\omega : S(\mathfrak {g}_n)^{\mathfrak {g}_n} \overset {\sim }{\longrightarrow } U(\mathfrak {g}_n)^{\mathfrak {g}_n} = Z(\mathfrak {g}_n)$
respects filtrations, we can describe the
$\omega : S(\mathfrak {g}_n)^{\mathfrak {g}_n} \overset {\sim }{\longrightarrow } U(\mathfrak {g}_n)^{\mathfrak {g}_n} = Z(\mathfrak {g}_n)$
respects filtrations, we can describe the
![]() $Z(\mathfrak {g}_n)$
.
$Z(\mathfrak {g}_n)$
.
Corollary 2.3
![]() $Z(\mathfrak {g}_n)$
is a polynomial algebra generated by
$Z(\mathfrak {g}_n)$
is a polynomial algebra generated by
![]() $(n+1)r$
elements
$(n+1)r$
elements
Proof Let
![]() $Z \subseteq Z(\mathfrak {g}_n)$
be the subalgebra generated by the elements (2.10). Since the inclusion
$Z \subseteq Z(\mathfrak {g}_n)$
be the subalgebra generated by the elements (2.10). Since the inclusion
![]() $\operatorname {gr} Z \subseteq \operatorname {gr} Z(\mathfrak {g}_n)$
is an equality, it follows that the inclusion
$\operatorname {gr} Z \subseteq \operatorname {gr} Z(\mathfrak {g}_n)$
is an equality, it follows that the inclusion
![]() $Z \subseteq Z(\mathfrak {g}_n)$
is also an equality. If these elements admit a nontrivial algebraic relation, then taking
$Z \subseteq Z(\mathfrak {g}_n)$
is also an equality. If these elements admit a nontrivial algebraic relation, then taking
![]() $\operatorname {gr}$
and using (2.9), we see that the elements (2.6) would admit a nontrivial relation. By Theorem 2.1, we see that (2.10) are algebraically independent.
$\operatorname {gr}$
and using (2.9), we see that the elements (2.6) would admit a nontrivial relation. By Theorem 2.1, we see that (2.10) are algebraically independent.
3 Category
 $\mathcal {O}$
for truncated current Lie algebras
$\mathcal {O}$
for truncated current Lie algebras
3.1 Definition and first properties of
 $\mathcal {O}$
$\mathcal {O}$
We begin by stating the definition of category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}_n$
.
$\mathfrak {g}_n$
.
Definition 3.1 The category
![]() $\mathcal {O}(\mathfrak {g}_n)$
is the full subcategory of
$\mathcal {O}(\mathfrak {g}_n)$
is the full subcategory of
![]() $U(\mathfrak {g}_n)$
-Mod with objects M satisfying the following:
$U(\mathfrak {g}_n)$
-Mod with objects M satisfying the following:
-
 $(\mathcal {O}1)$
M is finitely generated.
$(\mathcal {O}1)$
M is finitely generated. -
 $(\mathcal {O}2)$
$(\mathcal {O}2)$
 $\mathfrak {h}_n^0$
acts semisimply on M.
$\mathfrak {h}_n^0$
acts semisimply on M. -
 $(\mathcal {O}3)$
$(\mathcal {O}3)$
 $\mathfrak {h}_n^{\ge 1}\oplus \mathfrak {n}_n^+$
acts locally finitely on M.
$\mathfrak {h}_n^{\ge 1}\oplus \mathfrak {n}_n^+$
acts locally finitely on M.
Note that
![]() ${\mathcal {O}}(\mathfrak {g}_0)$
is nothing but the BGG category
${\mathcal {O}}(\mathfrak {g}_0)$
is nothing but the BGG category
![]() ${\mathcal {O}}$
for
${\mathcal {O}}$
for
![]() $\mathfrak {g}_0 = \mathfrak {g}$
.
$\mathfrak {g}_0 = \mathfrak {g}$
.
We refer the reader to [Reference HumphreysHu08] for a fairly comprehensive introduction to the algebraic study of
![]() ${\mathcal {O}}$
, and to [Reference Hotta, Takeuchi and TanisakiHTT08] for a discussion of the relationship between
${\mathcal {O}}$
, and to [Reference Hotta, Takeuchi and TanisakiHTT08] for a discussion of the relationship between
![]() ${\mathcal {O}}$
and
${\mathcal {O}}$
and
![]() $\mathcal {D}$
-modules on the flag variety.
$\mathcal {D}$
-modules on the flag variety.
It is not hard to see that
![]() $\mathcal {O}(\mathfrak {g}_n)$
is closed under submodules, quotients, and finite direct sums. Furthermore, by (
$\mathcal {O}(\mathfrak {g}_n)$
is closed under submodules, quotients, and finite direct sums. Furthermore, by (
![]() $\mathcal {O}1)$
, every
$\mathcal {O}1)$
, every
![]() $M \in \mathcal {O}(\mathfrak {g}_n)$
is Noetherian, since
$M \in \mathcal {O}(\mathfrak {g}_n)$
is Noetherian, since
![]() $U(\mathfrak {g}_n)$
is Noetherian.
$U(\mathfrak {g}_n)$
is Noetherian.
Let
![]() $M \in \mathcal {O}(\mathfrak {g}_n)$
and
$M \in \mathcal {O}(\mathfrak {g}_n)$
and
![]() $\lambda \in \mathfrak {h}^{*}$
. Define the weight space of weight
$\lambda \in \mathfrak {h}^{*}$
. Define the weight space of weight
![]() $\lambda $
by
$\lambda $
by
By (
![]() ${\mathcal {O}}2$
), we have
${\mathcal {O}}2$
), we have
![]() $M = \bigoplus _{\lambda \in \mathfrak {h}^{*}} M^\lambda $
, and this is a module grading of M, if we equip
$M = \bigoplus _{\lambda \in \mathfrak {h}^{*}} M^\lambda $
, and this is a module grading of M, if we equip
![]() $U(\mathfrak {g}_n)$
with its natural grading by the root lattice. The elements of
$U(\mathfrak {g}_n)$
with its natural grading by the root lattice. The elements of
![]() $M^\lambda $
are called weight vectors of weight
$M^\lambda $
are called weight vectors of weight
![]() $\lambda \in \mathfrak {h}^{*}$
. If
$\lambda \in \mathfrak {h}^{*}$
. If
![]() $m \in M^\lambda $
is a weight vector satisfying
$m \in M^\lambda $
is a weight vector satisfying
![]() $\mathfrak {n}_n^+ \cdot m = 0$
, then we say that m is a maximal vector of weight
$\mathfrak {n}_n^+ \cdot m = 0$
, then we say that m is a maximal vector of weight
![]() $\lambda $
.
$\lambda $
.
Now, let
![]() $\lambda \in \mathfrak {h}_n^{*}$
and recall that
$\lambda \in \mathfrak {h}_n^{*}$
and recall that
![]() $\lambda _i := \lambda |_{\mathfrak {h}_n^i}$
. We say that
$\lambda _i := \lambda |_{\mathfrak {h}_n^i}$
. We say that
![]() $m \in M^{\lambda _0}$
is a highest weight vector of weight
$m \in M^{\lambda _0}$
is a highest weight vector of weight
![]() $\lambda $
if m is maximal of weight
$\lambda $
if m is maximal of weight
![]() $\lambda $
and
$\lambda $
and
The following basic properties of weight spaces of
![]() $M \in {\mathcal {O}}(\mathfrak {g}_n)$
can be proven using the same argument as in BGG category
$M \in {\mathcal {O}}(\mathfrak {g}_n)$
can be proven using the same argument as in BGG category
![]() ${\mathcal {O}}$
(see [Reference HumphreysHu08, Section 1.1]):
${\mathcal {O}}$
(see [Reference HumphreysHu08, Section 1.1]):
 $$ \begin{align} \begin{array}{l} \dim(M^\lambda) < \infty \text{ for all } \lambda \in \mathfrak{h}^{*}, \\ \{\lambda \in \mathfrak{h}^{*} : M^{\lambda} \neq 0\} \subseteq \bigcup_{\lambda \in I} (\lambda - \mathbb{Z}_{\geq 0}\Phi^+) \text{ for some finite subset }I \subseteq \mathfrak{h}^{*}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l} \dim(M^\lambda) < \infty \text{ for all } \lambda \in \mathfrak{h}^{*}, \\ \{\lambda \in \mathfrak{h}^{*} : M^{\lambda} \neq 0\} \subseteq \bigcup_{\lambda \in I} (\lambda - \mathbb{Z}_{\geq 0}\Phi^+) \text{ for some finite subset }I \subseteq \mathfrak{h}^{*}. \end{array} \end{align} $$
If
![]() $m\in M \in {\mathcal {O}}(\mathfrak {g}_n)$
is a maximal vector, then we can find a highest weight vector in
$m\in M \in {\mathcal {O}}(\mathfrak {g}_n)$
is a maximal vector, then we can find a highest weight vector in
![]() $U(\mathfrak {h}_n) v$
thanks to
$U(\mathfrak {h}_n) v$
thanks to
![]() $({\mathcal {O}}3)$
. This proves the following result.
$({\mathcal {O}}3)$
. This proves the following result.
Lemma 3.2 [Reference ChaffeCh23, Corollary 3.3]
Suppose that
![]() $M \in \mathcal {O}$
admits a nonzero maximal vector of weight
$M \in \mathcal {O}$
admits a nonzero maximal vector of weight
![]() $\lambda \in \mathfrak {h}^{*}$
in M. Then M admits a nonzero highest weight vector of weight
$\lambda \in \mathfrak {h}^{*}$
in M. Then M admits a nonzero highest weight vector of weight
![]() $\mu $
for some
$\mu $
for some
![]() $\mu \in \mathfrak {h}_n^{*}$
satisfying
$\mu \in \mathfrak {h}_n^{*}$
satisfying
![]() $\mu _0 = \lambda $
.
$\mu _0 = \lambda $
.
3.2 Highest weight modules
We say M is a highest weight module of weight
![]() $\lambda \in \mathfrak {h}_n^{*}$
if M is generated by a highest weight vector of weight
$\lambda \in \mathfrak {h}_n^{*}$
if M is generated by a highest weight vector of weight
![]() $\lambda $
. The following result on highest weight filtrations is analogous to the situation for BGG category
$\lambda $
. The following result on highest weight filtrations is analogous to the situation for BGG category
![]() ${\mathcal {O}}$
(see [Reference HumphreysHu08, Corollary 1.2]). The proof is essentially the same as [Reference ChaffeCh23, Lemma 3.4].
${\mathcal {O}}$
(see [Reference HumphreysHu08, Corollary 1.2]). The proof is essentially the same as [Reference ChaffeCh23, Lemma 3.4].
Lemma 3.3 Let
![]() $M \in \mathcal {O}(\mathfrak {g}_n)$
. Then M has a finite filtration
$M \in \mathcal {O}(\mathfrak {g}_n)$
. Then M has a finite filtration
![]() $0 = M_0 \subseteq M_1 \subseteq \cdots \subseteq M_k = M$
such that each
$0 = M_0 \subseteq M_1 \subseteq \cdots \subseteq M_k = M$
such that each
![]() $M_{i+1}/M_i$
is a highest weight module. We call such a filtration a highest weight filtration.
$M_{i+1}/M_i$
is a highest weight module. We call such a filtration a highest weight filtration.
For
![]() $\lambda \in \mathfrak {h}_n^{*}$
, we define the Verma module of weight
$\lambda \in \mathfrak {h}_n^{*}$
, we define the Verma module of weight
![]() $\lambda $
via
$\lambda $
via
where
![]() $\mathbb {C}_{\lambda }$
is the one dimensional
$\mathbb {C}_{\lambda }$
is the one dimensional
![]() $U(\mathfrak {b}_n)$
-module upon which
$U(\mathfrak {b}_n)$
-module upon which
![]() $\mathfrak {h}_n$
acts via
$\mathfrak {h}_n$
acts via
![]() $\lambda $
, and
$\lambda $
, and
![]() $\mathfrak {n}_n$
acts by 0. The Verma modules are the universal highest weight modules, in the sense that every highest weight module is a quotient of a Verma module.
$\mathfrak {n}_n$
acts by 0. The Verma modules are the universal highest weight modules, in the sense that every highest weight module is a quotient of a Verma module.
They enjoy the following nice properties, generalizing the classical case
![]() $n = 0$
(see [Reference HumphreysHu08, Section 1]):
$n = 0$
(see [Reference HumphreysHu08, Section 1]):
-
(1)
 $\dim M_{\lambda }^{\lambda _0}= 1$
, and hence
$\dim M_{\lambda }^{\lambda _0}= 1$
, and hence
 $\dim M^{\lambda _0} = 1$
for every highest weight module of weight
$\dim M^{\lambda _0} = 1$
for every highest weight module of weight
 $\lambda \in \mathfrak {h}_n^{*}$
.
$\lambda \in \mathfrak {h}_n^{*}$
. -
(2) Every highest weight module M admits a central character: for every
 $\lambda \in \mathfrak {h}_n^{*}$
, there is a homomorphism
$\lambda \in \mathfrak {h}_n^{*}$
, there is a homomorphism
 $\chi _\lambda : Z(\mathfrak {g}_n) \to \mathbb {C}$
such that
$\chi _\lambda : Z(\mathfrak {g}_n) \to \mathbb {C}$
such that
 $z\cdot m = \chi _\lambda (z) m$
for all
$z\cdot m = \chi _\lambda (z) m$
for all
 $z\in Z(\mathfrak {g}_n)$
and all
$z\in Z(\mathfrak {g}_n)$
and all
 $m \in M$
where M is a highest weight module, of weight
$m \in M$
where M is a highest weight module, of weight
 $\lambda $
.
$\lambda $
. -
(3)
 $M_\lambda $
admits a unique maximal submodule and a unique simple quotient, which we denote
$M_\lambda $
admits a unique maximal submodule and a unique simple quotient, which we denote
 $L_\lambda $
.
$L_\lambda $
. -
(4) Every simple object in
 ${\mathcal {O}}(\mathfrak {g}_n)$
is isomorphic to precisely one of these simple modules (by Lemma 3.3). Thus, the modules give a complete set of representatives for the isomorphism classes of simple modules in
${\mathcal {O}}(\mathfrak {g}_n)$
is isomorphic to precisely one of these simple modules (by Lemma 3.3). Thus, the modules give a complete set of representatives for the isomorphism classes of simple modules in $$ \begin{align*}\{L_{\lambda} \mid \lambda \in \mathfrak{h}_n^{*}\}\end{align*} $$
$$ \begin{align*}\{L_{\lambda} \mid \lambda \in \mathfrak{h}_n^{*}\}\end{align*} $$
 ${\mathcal {O}}(\mathfrak {g}_n)$
.
${\mathcal {O}}(\mathfrak {g}_n)$
.
3.3 Jordan decomposition for
 $\mathcal {O}(\mathfrak {g}_n)$
$\mathcal {O}(\mathfrak {g}_n)$
The standard approach to studying modules in BGG category
![]() ${\mathcal {O}}$
is to consider modules with a fixed central character for
${\mathcal {O}}$
is to consider modules with a fixed central character for
![]() $U(\mathfrak {g})$
. This refinement is also useful in our more general setting (see Theorem 4.2); however, as a first approximation, we decompose
$U(\mathfrak {g})$
. This refinement is also useful in our more general setting (see Theorem 4.2); however, as a first approximation, we decompose
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
in terms of generalized eigenvalues for
${\mathcal {O}}(\mathfrak {g}_n)$
in terms of generalized eigenvalues for
![]() $\mathfrak {h}_n^{\ge 1}$
.
$\mathfrak {h}_n^{\ge 1}$
.
Fix
![]() $M \in {\mathcal {O}}(\mathfrak {g}_n)$
and
$M \in {\mathcal {O}}(\mathfrak {g}_n)$
and
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
. We define the generalized eigenspace of eigenvalue
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
. We define the generalized eigenspace of eigenvalue
![]() $\mu $
via
$\mu $
via
The following result is a slight generalization of [Reference ChaffeCh23, Lemma 3.7], and we supply a sketch of the proof for the reader’s convenience.
Lemma 3.4 Every
![]() $M \in \mathcal {O}(\mathfrak {g}_n)$
admits a direct sum decomposition of
$M \in \mathcal {O}(\mathfrak {g}_n)$
admits a direct sum decomposition of
![]() $\mathfrak {g}_n$
-modules
$\mathfrak {g}_n$
-modules
Proof Since
![]() $\mathfrak {h}_n$
preserves the weight spaces of M, which are finite-dimensional, it follows that each
$\mathfrak {h}_n$
preserves the weight spaces of M, which are finite-dimensional, it follows that each
![]() $M^\lambda $
decomposes into generalized eigenspaces for
$M^\lambda $
decomposes into generalized eigenspaces for
![]() $\mathfrak {h}_n^{\ge 1}$
. Therefore, M admits a decomposition (3.5), and it suffices to show that each summand is a
$\mathfrak {h}_n^{\ge 1}$
. Therefore, M admits a decomposition (3.5), and it suffices to show that each summand is a
![]() $\mathfrak {g}_n$
-module. This follows by a direct calculation, using the fact that
$\mathfrak {g}_n$
-module. This follows by a direct calculation, using the fact that
![]() $\mathfrak {g}$
admits an eigenbasis for
$\mathfrak {g}$
admits an eigenbasis for
![]() $\mathfrak {h}$
(root space decomposition) and
$\mathfrak {h}$
(root space decomposition) and
![]() $\mathfrak {h}_n^{\ge 1}$
acts nilpotently on
$\mathfrak {h}_n^{\ge 1}$
acts nilpotently on
![]() $\mathfrak {g}_n$
.
$\mathfrak {g}_n$
.
Now, we define the Jordan block of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
of weight
${\mathcal {O}}(\mathfrak {g}_n)$
of weight
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
to be the full subcategory
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
to be the full subcategory
![]() $\mathcal {O}(\mathfrak {g}_n)$
whose objects are the modules M such that
$\mathcal {O}(\mathfrak {g}_n)$
whose objects are the modules M such that
![]() $M = M^{(\mu )}$
. We then have the following Jordan decomposition:
$M = M^{(\mu )}$
. We then have the following Jordan decomposition:
Remark 3.5 It is not hard to see that if
![]() $\lambda \in \mathfrak {h}_n^{*}$
and
$\lambda \in \mathfrak {h}_n^{*}$
and
![]() $\mu = \lambda |_{\mathfrak {h}_n^{\ge 1}}$
, then both
$\mu = \lambda |_{\mathfrak {h}_n^{\ge 1}}$
, then both
![]() $M_{\lambda }$
and
$M_{\lambda }$
and
![]() $L_\lambda $
lie in
$L_\lambda $
lie in
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
(see also [Reference ChaffeCh23, Lemma 3.9]). Combining (3.6) with the fact that Verma modules have unique maximal submodules, and are therefore indecomposable, it follows that
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
(see also [Reference ChaffeCh23, Lemma 3.9]). Combining (3.6) with the fact that Verma modules have unique maximal submodules, and are therefore indecomposable, it follows that
![]() $L_{\lambda }$
cannot occur as a subquotient of
$L_{\lambda }$
cannot occur as a subquotient of
![]() $M_{\nu }$
unless
$M_{\nu }$
unless
![]() $\lambda _{\ge 1} = \nu _{\ge 1}$
.
$\lambda _{\ge 1} = \nu _{\ge 1}$
.
Let
![]() $\mathfrak {g}_n \to \mathfrak {g}_{n-1}$
be the natural quotient map with kernel
$\mathfrak {g}_n \to \mathfrak {g}_{n-1}$
be the natural quotient map with kernel
![]() $\mathfrak {g}_n^n$
, and consider the pullback functor
$\mathfrak {g}_n^n$
, and consider the pullback functor
Lemma 3.6 Let
![]() $\lambda \in \mathfrak {h}_{n-1}^{*}$
and define
$\lambda \in \mathfrak {h}_{n-1}^{*}$
and define
![]() $\nu \in \mathfrak {h}_n^{*}$
by
$\nu \in \mathfrak {h}_n^{*}$
by
![]() $\nu (h_i) = \lambda (h_i)$
for
$\nu (h_i) = \lambda (h_i)$
for
![]() $i=0,...,n-1$
and
$i=0,...,n-1$
and
![]() $\nu (h_n) = 0$
for all
$\nu (h_n) = 0$
for all
![]() $h \in \mathfrak {h}$
. Then
$h \in \mathfrak {h}$
. Then
![]() $p(L_\lambda )\cong L_{\nu }$
as
$p(L_\lambda )\cong L_{\nu }$
as
![]() $\mathfrak {g}_n$
-modules.
$\mathfrak {g}_n$
-modules.
Proof Certainly,
![]() $p(L_\lambda )$
is a simple highest weight module of highest weight
$p(L_\lambda )$
is a simple highest weight module of highest weight
![]() $\nu $
, and the proof follows.
$\nu $
, and the proof follows.
Now, we state and prove some easy equivalences between Jordan blocks of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
which arise by tensoring with one-dimensional
${\mathcal {O}}(\mathfrak {g}_n)$
which arise by tensoring with one-dimensional
![]() $\mathfrak {g}_n$
-modules. We write
$\mathfrak {g}_n$
-modules. We write
![]() $\mathfrak {g}' = [\mathfrak {g},\mathfrak {g}]$
for the derived subalgebra. We note that
$\mathfrak {g}' = [\mathfrak {g},\mathfrak {g}]$
for the derived subalgebra. We note that
![]() $(\mathfrak {g}_n)' = (\mathfrak {g}')_n$
, and so we may use the notation
$(\mathfrak {g}_n)' = (\mathfrak {g}')_n$
, and so we may use the notation
![]() $\mathfrak {g}_n^{\prime }$
unambiguously.
$\mathfrak {g}_n^{\prime }$
unambiguously.
For
![]() $\lambda \in \mathfrak {h}_n^{*}$
, we recall the notation
$\lambda \in \mathfrak {h}_n^{*}$
, we recall the notation
![]() $\lambda _{\ge 1}:=\lambda |_{\mathfrak {h}_n^{\ge 1}}$
. Any such
$\lambda _{\ge 1}:=\lambda |_{\mathfrak {h}_n^{\ge 1}}$
. Any such
![]() $\lambda $
can be extended to an element of
$\lambda $
can be extended to an element of
![]() $\mathfrak {g}_n^{*}$
via
$\mathfrak {g}_n^{*}$
via
![]() $\lambda (\mathfrak {n}_n^{\pm }) = 0$
, and we may abuse notation by identifying
$\lambda (\mathfrak {n}_n^{\pm }) = 0$
, and we may abuse notation by identifying
![]() $\mathfrak {h}_n^{*}$
with a subspace of
$\mathfrak {h}_n^{*}$
with a subspace of
![]() $\mathfrak {g}_n^{*}$
. For
$\mathfrak {g}_n^{*}$
. For
![]() $\lambda \in \operatorname {Ann}_{\mathfrak {g}^{*}_n} (\mathfrak {g}^{\prime }_n)$
, let
$\lambda \in \operatorname {Ann}_{\mathfrak {g}^{*}_n} (\mathfrak {g}^{\prime }_n)$
, let
![]() $\mathbb {C}_{\lambda }$
be the one-dimensional
$\mathbb {C}_{\lambda }$
be the one-dimensional
![]() $\mathfrak {g}_n$
-module afforded by
$\mathfrak {g}_n$
-module afforded by
![]() $\lambda $
.
$\lambda $
.
Lemma 3.7 Suppose that
![]() $\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
$\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
![]() $\lambda |_{\mathfrak {g}_n^{\prime }} = \nu |_{\mathfrak {g}_n^{\prime }}$
. Then
$\lambda |_{\mathfrak {g}_n^{\prime }} = \nu |_{\mathfrak {g}_n^{\prime }}$
. Then
![]() $(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\lambda - \nu }$
and
$(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\lambda - \nu }$
and
![]() $(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\nu - \lambda }$
are quasi-inverse equivalences between
$(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\nu - \lambda }$
are quasi-inverse equivalences between
![]() ${\mathcal {O}}^{(\lambda _{\ge 1})}(\mathfrak {g}_n)$
and
${\mathcal {O}}^{(\lambda _{\ge 1})}(\mathfrak {g}_n)$
and
![]() ${\mathcal {O}}^{(\nu _{\ge 1})}(\mathfrak {g}_n)$
.
${\mathcal {O}}^{(\nu _{\ge 1})}(\mathfrak {g}_n)$
.
Proof Since
![]() $\pm (\lambda - \nu )$
vanishes on
$\pm (\lambda - \nu )$
vanishes on
![]() $\mathfrak {g}_n^{\prime }$
, it defines a one-dimensional representation of
$\mathfrak {g}_n^{\prime }$
, it defines a one-dimensional representation of
![]() $\mathfrak {g}_n$
, and the named functors are quasi-inverse autoequivalences of
$\mathfrak {g}_n$
, and the named functors are quasi-inverse autoequivalences of
![]() $\mathfrak {g}_n\operatorname {-mod}$
. To complete the proof, it suffices to observe that
$\mathfrak {g}_n\operatorname {-mod}$
. To complete the proof, it suffices to observe that
![]() $(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\lambda - \nu }$
sends
$(\bullet) \otimes _{U(\mathfrak {g}_n)} \mathbb {C}_{\lambda - \nu }$
sends
![]() ${\mathcal {O}}^{(\lambda _{\ge 1})}(\mathfrak {g}_n)$
to
${\mathcal {O}}^{(\lambda _{\ge 1})}(\mathfrak {g}_n)$
to
![]() ${\mathcal {O}}^{(\nu _{\ge 1})}(\mathfrak {g}_n)$
, which follows directly from the definitions.
${\mathcal {O}}^{(\nu _{\ge 1})}(\mathfrak {g}_n)$
, which follows directly from the definitions.
4 Parabolic induction
In this section, we prove Theorem 1.2, which allows us to relate the category
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
with a Jordan block of
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
with a Jordan block of
![]() ${\mathcal {O}}({\mathfrak {l}}_n)$
for a Levi subalgebra
${\mathcal {O}}({\mathfrak {l}}_n)$
for a Levi subalgebra
![]() ${\mathfrak {l}}$
. Recall that if
${\mathfrak {l}}$
. Recall that if
![]() $\nu \in \mathfrak {h}^{*}$
, then we extend
$\nu \in \mathfrak {h}^{*}$
, then we extend
![]() $\nu $
to an element of
$\nu $
to an element of
![]() $\mathfrak {g}^{*}$
via
$\mathfrak {g}^{*}$
via
![]() $\nu (\mathfrak {n}^\pm ) = 0$
, and write
$\nu (\mathfrak {n}^\pm ) = 0$
, and write
![]() $\mathfrak {g}^\nu $
for the coadjoint centralizer.
$\mathfrak {g}^\nu $
for the coadjoint centralizer.
Theorem 4.1 Let
![]() $\lambda \in \mathfrak {h}_n^{*}$
. Suppose that the centralizer
$\lambda \in \mathfrak {h}_n^{*}$
. Suppose that the centralizer
![]() ${\mathfrak {l}} = \mathfrak {g}^{\lambda _n}$
is in standard Levi form and let
${\mathfrak {l}} = \mathfrak {g}^{\lambda _n}$
is in standard Levi form and let
![]() $\mathfrak {p} := {\mathfrak {l}} + \mathfrak {n}^+ = {\mathfrak {l}} \oplus {\mathfrak {r}}$
be a parabolic subalgebra with Levi factor
$\mathfrak {p} := {\mathfrak {l}} + \mathfrak {n}^+ = {\mathfrak {l}} \oplus {\mathfrak {r}}$
be a parabolic subalgebra with Levi factor
![]() ${\mathfrak {l}}$
and nilradical
${\mathfrak {l}}$
and nilradical
![]() ${\mathfrak {r}}$
. Write
${\mathfrak {r}}$
. Write
![]() $\mu = \lambda _{\ge 1}$
(notation (2.3)). The categories
$\mu = \lambda _{\ge 1}$
(notation (2.3)). The categories
![]() $\mathcal {O}^{(\mu )}({\mathfrak {l}}_n)$
and
$\mathcal {O}^{(\mu )}({\mathfrak {l}}_n)$
and
![]() $\mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
are equivalent. The quasi-inverse functors inducing the equivalence are parabolic induction and
$\mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
are equivalent. The quasi-inverse functors inducing the equivalence are parabolic induction and
![]() ${\mathfrak {r}}_n$
-invariants:
${\mathfrak {r}}_n$
-invariants:
 $$ \begin{align*} \begin{array}{rcccl} \operatorname{Ind} & : & \mathcal{O}^{(\mu)} ({\mathfrak{l}}_n) &\longrightarrow & \mathcal{O}^{(\mu)} (\mathfrak{g}_n) \\ & & M &\longmapsto & U(\mathfrak{g}_n) \otimes_{U(\mathfrak{p}_n)} M, \\ (\bullet)^{{\mathfrak{r}}_n} & : & \mathcal{O}^{(\mu)} (\mathfrak{g}_n) &\longrightarrow & \mathcal{O}^{(\mu)} ({\mathfrak{l}}_n) \\ & & M &\longmapsto & M^{\mathfrak{r}_n}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcccl} \operatorname{Ind} & : & \mathcal{O}^{(\mu)} ({\mathfrak{l}}_n) &\longrightarrow & \mathcal{O}^{(\mu)} (\mathfrak{g}_n) \\ & & M &\longmapsto & U(\mathfrak{g}_n) \otimes_{U(\mathfrak{p}_n)} M, \\ (\bullet)^{{\mathfrak{r}}_n} & : & \mathcal{O}^{(\mu)} (\mathfrak{g}_n) &\longrightarrow & \mathcal{O}^{(\mu)} ({\mathfrak{l}}_n) \\ & & M &\longmapsto & M^{\mathfrak{r}_n}. \end{array} \end{align*} $$
Theorem 4.1 is inspired by a category equivalence in modular representation theory due to Friedlander and Parshall [Reference Friedlander and ParshallFP88, Theorem 2.1]. The case
![]() $n = 1$
is due to the first author [Reference ChaffeCh23], and our method here is a generalization of loc. cit.
$n = 1$
is due to the first author [Reference ChaffeCh23], and our method here is a generalization of loc. cit.
We observe that
![]() $\operatorname {Ind}$
is left adjoint to
$\operatorname {Ind}$
is left adjoint to
![]() $(\bullet)^{{\mathfrak {r}}_n}$
since we have inverse isomorphisms
$(\bullet)^{{\mathfrak {r}}_n}$
since we have inverse isomorphisms
 $$ \begin{align*} \operatorname{Hom}_{{\mathfrak{l}}_n}(M, N^{\mathfrak{r}_n}) \underset{\eta}{\overset{\theta}{{\mathrel{\substack{\xrightarrow{{\rule{1cm}{0cm}}} \\[-.9ex] \xleftarrow{{\rule{1cm}{0cm}}}}}}}} \operatorname{Hom}_{\mathfrak{g}_n}(\operatorname{Ind} M, N) \end{align*} $$
$$ \begin{align*} \operatorname{Hom}_{{\mathfrak{l}}_n}(M, N^{\mathfrak{r}_n}) \underset{\eta}{\overset{\theta}{{\mathrel{\substack{\xrightarrow{{\rule{1cm}{0cm}}} \\[-.9ex] \xleftarrow{{\rule{1cm}{0cm}}}}}}}} \operatorname{Hom}_{\mathfrak{g}_n}(\operatorname{Ind} M, N) \end{align*} $$
given by
![]() $\theta (f)(u \otimes m) = u \cdot f(m)$
and
$\theta (f)(u \otimes m) = u \cdot f(m)$
and
![]() $\eta (g)(m) = g(1 \otimes m)$
for
$\eta (g)(m) = g(1 \otimes m)$
for
![]() $u\in U(\mathfrak {g}_n)$
and
$u\in U(\mathfrak {g}_n)$
and
![]() $m \in M$
.
$m \in M$
.
Let
![]() denote the identity endofunctor of a category
denote the identity endofunctor of a category
![]() $\mathcal {C}$
. In order to show that the adjoint functors
$\mathcal {C}$
. In order to show that the adjoint functors
![]() $\operatorname {Ind}$
and
$\operatorname {Ind}$
and
![]() $(\bullet)^{{\mathfrak {r}}_n}$
are equivalences, we consider the unit and counit of the adjunction. The unit is the natural transformation
$(\bullet)^{{\mathfrak {r}}_n}$
are equivalences, we consider the unit and counit of the adjunction. The unit is the natural transformation
![]() , which is obtained by applying
, which is obtained by applying
![]() $\eta $
to the identity mapping
$\eta $
to the identity mapping
![]() $N^{{\mathfrak {r}}_n} \to N^{{\mathfrak {r}}_n}$
, while the counit is the natural transformation
$N^{{\mathfrak {r}}_n} \to N^{{\mathfrak {r}}_n}$
, while the counit is the natural transformation
![]() obtained by applying
obtained by applying
![]() $\theta $
to the identity mapping
$\theta $
to the identity mapping
![]() $\operatorname {Ind} M \to \operatorname {Ind} M$
. In particular, we have
$\operatorname {Ind} M \to \operatorname {Ind} M$
. In particular, we have
 $$ \begin{align} \begin{array}{rcl} \psi_M &:& M \longrightarrow (\operatorname{Ind} M)^{\mathfrak{r}_n}\\ & & m \longmapsto 1\otimes m, \\ \varphi_N & : & \operatorname{Ind} (N^{\mathfrak{r}_n}) \longrightarrow N\\ & & u\otimes m \longmapsto u\cdot m. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcl} \psi_M &:& M \longrightarrow (\operatorname{Ind} M)^{\mathfrak{r}_n}\\ & & m \longmapsto 1\otimes m, \\ \varphi_N & : & \operatorname{Ind} (N^{\mathfrak{r}_n}) \longrightarrow N\\ & & u\otimes m \longmapsto u\cdot m. \end{array} \end{align} $$
In order to complete the proof of Theorem 4.1, it suffices to show that
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
are both natural equivalences. The proof, which is given is Section 4.2, depends heavily on the exactness of
$\varphi $
are both natural equivalences. The proof, which is given is Section 4.2, depends heavily on the exactness of
![]() $(\bullet)^{{\mathfrak {r}}_n}$
, which will occupy the majority of Sections 4.1 and 4.2.
$(\bullet)^{{\mathfrak {r}}_n}$
, which will occupy the majority of Sections 4.1 and 4.2.
4.1 Central characters
If two
![]() $\mathfrak {g}_n$
-modules admit different infinitesimal central characters, then there can be no extensions between them. The main step in proving exactness of
$\mathfrak {g}_n$
-modules admit different infinitesimal central characters, then there can be no extensions between them. The main step in proving exactness of
![]() $(\bullet)^{{\mathfrak {r}}_n}$
is the following result, which leads to a vanishing criterion for extensions. For
$(\bullet)^{{\mathfrak {r}}_n}$
is the following result, which leads to a vanishing criterion for extensions. For
![]() $\nu \in \mathfrak {h}^{*}$
, we make the notation
$\nu \in \mathfrak {h}^{*}$
, we make the notation
For
![]() $\lambda \in \mathfrak {h}_n^{*}$
, recall the notation
$\lambda \in \mathfrak {h}_n^{*}$
, recall the notation
![]() $\chi _\lambda $
for central characters, introduced in Section 3.2(2).
$\chi _\lambda $
for central characters, introduced in Section 3.2(2).
Theorem 4.2 Let
![]() $\lambda , \lambda ' \in \mathfrak {h}^{*}_n$
such that
$\lambda , \lambda ' \in \mathfrak {h}^{*}_n$
such that
![]() $\lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
and
$\lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
and
![]() $\mathfrak {g}^{\lambda _n}$
is in standard Levi form. Then
$\mathfrak {g}^{\lambda _n}$
is in standard Levi form. Then
![]() $\chi _\lambda = \chi _{\lambda '}$
if and only if
$\chi _\lambda = \chi _{\lambda '}$
if and only if
![]() $\lambda _0 - \lambda ^{\prime }_0 \in \mathbb {C}\Phi _{\lambda _n}$
.
$\lambda _0 - \lambda ^{\prime }_0 \in \mathbb {C}\Phi _{\lambda _n}$
.
Corollary 4.3 If
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
is indecomposable and
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
is indecomposable and
![]() $\mathfrak {g}^{\mu _n}$
is in standard Levi form, then there is a unique coset
$\mathfrak {g}^{\mu _n}$
is in standard Levi form, then there is a unique coset
![]() $\Xi _M \in \mathfrak {h}^{*}/ \mathbb {C}\Phi _{\mu _n}$
such that if N is a highest weight subquotient of M of weight
$\Xi _M \in \mathfrak {h}^{*}/ \mathbb {C}\Phi _{\mu _n}$
such that if N is a highest weight subquotient of M of weight
![]() $\lambda \in \mathfrak {h}_n^{*}$
, then
$\lambda \in \mathfrak {h}_n^{*}$
, then
![]() $\lambda _{\ge 1} = \mu $
and
$\lambda _{\ge 1} = \mu $
and
![]() $\lambda _0 + \mathbb {C}\Phi _{\mu _n} = \Xi _M$
.
$\lambda _0 + \mathbb {C}\Phi _{\mu _n} = \Xi _M$
.
Before we proceed, we explain how to deduce the corollary from Theorem 4.2. Using the Jordan decomposition from Lemma 3.4 along with Remark 3.5, we see that all subquotients of an indecomposable module lie in the same Jordan block
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
, which confirms that
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
, which confirms that
![]() $\lambda _{\ge 1} = \mu $
. Since M has finite-dimensional weight spaces (3.3) and is indecomposable, it admits a generalized central character, i.e., there is a unique maximal ideal
$\lambda _{\ge 1} = \mu $
. Since M has finite-dimensional weight spaces (3.3) and is indecomposable, it admits a generalized central character, i.e., there is a unique maximal ideal
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() $Z(\mathfrak {g}_n)$
such that
$Z(\mathfrak {g}_n)$
such that
![]() $\mathfrak {m}^k M = 0$
for
$\mathfrak {m}^k M = 0$
for
![]() $k \gg 0$
. Thus, all of the highest weight subquotients have the same central character (Section 3.2(2)). Now, Corollary 4.3 follows from Theorem 4.2.
$k \gg 0$
. Thus, all of the highest weight subquotients have the same central character (Section 3.2(2)). Now, Corollary 4.3 follows from Theorem 4.2.
Remark 4.4 Later, we shall see that Theorem 4.2 and Corollary 4.3 hold without the standard Levi-type hypothesis. This follows from Theorem 1.3. However, since the latter theorem relies on Theorem 4.2, we retain this hypothesis to keep these dependences clear.
We now proceed to prove Theorem 4.2. Recall from Section 2.2 that the symmetric invariants
![]() $S(\mathfrak {g})^{\mathfrak {g}}$
are generated by algebraically independent homogeneous elements
$S(\mathfrak {g})^{\mathfrak {g}}$
are generated by algebraically independent homogeneous elements
![]() $p_1,...,p_r$
. Furthermore, there is an embedding
$p_1,...,p_r$
. Furthermore, there is an embedding
![]() $S(\mathfrak {g})^{\mathfrak {g}} \hookrightarrow S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
such that
$S(\mathfrak {g})^{\mathfrak {g}} \hookrightarrow S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
such that
![]() $S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
is generated by
$S(\mathfrak {g}_n)^{\mathfrak {g}_n}$
is generated by
![]() $r(n+1)$
elements
$r(n+1)$
elements
![]() $\partial ^{(k)} p_j, \ j=1,...,r, \ k =0,...,n$
. There is a linear map
$\partial ^{(k)} p_j, \ j=1,...,r, \ k =0,...,n$
. There is a linear map
![]() $\omega : S(\mathfrak {g}_n)^{\mathfrak {g}_n} \to Z(\mathfrak {g}_n)$
, and we will be especially interested in the central elements
$\omega : S(\mathfrak {g}_n)^{\mathfrak {g}_n} \to Z(\mathfrak {g}_n)$
, and we will be especially interested in the central elements
Now, let
![]() $U(\mathfrak {g}_n)^{\mathfrak {h}}$
be the invariant subalgebra under the adjoint action of
$U(\mathfrak {g}_n)^{\mathfrak {h}}$
be the invariant subalgebra under the adjoint action of
![]() $\mathfrak {h}$
. Also, let
$\mathfrak {h}$
. Also, let
![]() $U(\mathfrak {g}_n) \mathfrak {n}_n^+$
be the left ideal generated by
$U(\mathfrak {g}_n) \mathfrak {n}_n^+$
be the left ideal generated by
![]() $\mathfrak {n}_n^+$
. The intersection
$\mathfrak {n}_n^+$
. The intersection
![]() $U(\mathfrak {g}_n) \mathfrak {n}_n^+ \cap U(\mathfrak {g}_n)^{\mathfrak {h}}$
is actually an ideal of
$U(\mathfrak {g}_n) \mathfrak {n}_n^+ \cap U(\mathfrak {g}_n)^{\mathfrak {h}}$
is actually an ideal of
![]() $U(\mathfrak {g}_n)^{\mathfrak {h}}$
, and it is not hard to see that the quotient by this ideal is isomorphic to
$U(\mathfrak {g}_n)^{\mathfrak {h}}$
, and it is not hard to see that the quotient by this ideal is isomorphic to
![]() $U(\mathfrak {h}_n)$
. Following the observations of [Reference HumphreysHu08, Section 1.7] verbatim, we see that
$U(\mathfrak {h}_n)$
. Following the observations of [Reference HumphreysHu08, Section 1.7] verbatim, we see that
![]() $\chi _\lambda $
coincides with the composition
$\chi _\lambda $
coincides with the composition
where
![]() $\operatorname {ev}_\lambda $
denotes evaluation at
$\operatorname {ev}_\lambda $
denotes evaluation at
![]() $\lambda $
. This allows us to consider
$\lambda $
. This allows us to consider
![]() $\chi _\lambda (p)$
for any
$\chi _\lambda (p)$
for any
![]() $p \in U(\mathfrak {g}_n)^{\mathfrak {h}}$
, not just
$p \in U(\mathfrak {g}_n)^{\mathfrak {h}}$
, not just
![]() $p \in Z(\mathfrak {g}_n)$
.
$p \in Z(\mathfrak {g}_n)$
.
Now, for
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, we define two maps
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
, we define two maps
![]() $\mathfrak {h}^{*} \to \mathbb {C}^r$
. For
$\mathfrak {h}^{*} \to \mathbb {C}^r$
. For
![]() $\nu \in \mathfrak {h}^{*}$
, we use the notation
$\nu \in \mathfrak {h}^{*}$
, we use the notation
![]() $(\nu , \mu )$
to denote the element of
$(\nu , \mu )$
to denote the element of
![]() $\mathfrak {h}_n^{*}$
which restricts as
$\mathfrak {h}_n^{*}$
which restricts as
![]() $\nu $
on
$\nu $
on
![]() $\mathfrak {h}_n^0$
and to
$\mathfrak {h}_n^0$
and to
![]() $\mu $
on
$\mu $
on
![]() $\mathfrak {h}_n^{\ge 1}$
. The first map is
$\mathfrak {h}_n^{\ge 1}$
. The first map is
while the second is
where
![]() $\theta _{(\nu , \mu )}$
denotes the composition
$\theta _{(\nu , \mu )}$
denotes the composition
and
![]() $\mathbb {C}[\mathfrak {g}^{*}] \to \mathbb {C}[\mathfrak {h}^{*}]$
is restriction across the triangular decomposition of
$\mathbb {C}[\mathfrak {g}^{*}] \to \mathbb {C}[\mathfrak {h}^{*}]$
is restriction across the triangular decomposition of
![]() $\mathfrak {g}^{*}$
, while the second map is the restriction of
$\mathfrak {g}^{*}$
, while the second map is the restriction of
![]() $d^{(n)}$
to
$d^{(n)}$
to
![]() $\mathbb {C}[\mathfrak {h}^{*}]$
and the third map is evaluation
$\mathbb {C}[\mathfrak {h}^{*}]$
and the third map is evaluation
![]() $\operatorname {ev}_{(\nu , \mu )}$
.
$\operatorname {ev}_{(\nu , \mu )}$
.
Lemma 4.5
![]() $\xi _\mu (\nu ) - \eta _\mu (\nu )$
depends only on
$\xi _\mu (\nu ) - \eta _\mu (\nu )$
depends only on
![]() $\mu $
.
$\mu $
.
Proof Note that we have a Lie algebra embedding
![]() $\mathfrak {g}_1 \hookrightarrow \mathfrak {g}_n$
given by
$\mathfrak {g}_1 \hookrightarrow \mathfrak {g}_n$
given by
![]() $x_0 \mapsto x_0$
and
$x_0 \mapsto x_0$
and
![]() $x_1 \mapsto x_n$
for all
$x_1 \mapsto x_n$
for all
![]() $x\in \mathfrak {g}$
. We have
$x\in \mathfrak {g}$
. We have
![]() $\xi _\mu (\nu ) - \eta _\mu (\nu ) \in S(\mathfrak {g}_1) \subseteq S(\mathfrak {g}_n)$
, and this reduces the claim to the case
$\xi _\mu (\nu ) - \eta _\mu (\nu ) \in S(\mathfrak {g}_1) \subseteq S(\mathfrak {g}_n)$
, and this reduces the claim to the case
![]() $n = 1$
. This was proven in [Reference ChaffeCh23, Lemma 4.6(b)].
$n = 1$
. This was proven in [Reference ChaffeCh23, Lemma 4.6(b)].
Lemma 4.6 For
![]() $\lambda , \lambda ' \in \mathfrak {h}_n^{*}$
satisfying
$\lambda , \lambda ' \in \mathfrak {h}_n^{*}$
satisfying
![]() $\lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
, we have
$\lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
, we have
![]() $\chi _\lambda = \chi _{\lambda '}$
if and only if
$\chi _\lambda = \chi _{\lambda '}$
if and only if
![]() $\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
for
$\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
for
![]() $i=1,...,r$
.
$i=1,...,r$
.
Proof Since the center
![]() $Z(\mathfrak {g}_n)$
is generated by the elements
$Z(\mathfrak {g}_n)$
is generated by the elements
![]() $\omega (\partial ^{(k)} p_j)$
, it follows that
$\omega (\partial ^{(k)} p_j)$
, it follows that
![]() $\chi _\lambda = \chi _{\lambda '}$
if and only if the characters coincide on these elements. Thus, if we can show that
$\chi _\lambda = \chi _{\lambda '}$
if and only if the characters coincide on these elements. Thus, if we can show that
![]() $\chi _\lambda (z_i^{(j)}) = \chi _{\lambda '}(z_i^{(j)})$
for all
$\chi _\lambda (z_i^{(j)}) = \chi _{\lambda '}(z_i^{(j)})$
for all
![]() $j=0,...,n-1$
, then the proof will be complete.
$j=0,...,n-1$
, then the proof will be complete.
We have
![]() $p_i \in S(\mathfrak {g}_n^n)$
, and it follows from (2.4) and (2.5) that
$p_i \in S(\mathfrak {g}_n^n)$
, and it follows from (2.4) and (2.5) that
![]() $\partial ^{(j)}p_i \in S(\mathfrak {g}_n^{\ge n-j})$
. By the definition of
$\partial ^{(j)}p_i \in S(\mathfrak {g}_n^{\ge n-j})$
. By the definition of
![]() $\omega $
(2.8), we have
$\omega $
(2.8), we have
![]() $z_i^{(j)} \in U(\mathfrak {g}_n^{\ge n-j})$
. Therefore,
$z_i^{(j)} \in U(\mathfrak {g}_n^{\ge n-j})$
. Therefore,
![]() $\chi _\lambda (z_i^{(j)})$
only depends on
$\chi _\lambda (z_i^{(j)})$
only depends on
![]() $\lambda _{\ge n-j}$
. Since
$\lambda _{\ge n-j}$
. Since
![]() $\chi _\lambda $
is precisely the composition (4.2), we have reached the desired conclusion. This completes the proof.
$\chi _\lambda $
is precisely the composition (4.2), we have reached the desired conclusion. This completes the proof.
Proof of Theorem 4.2
Let
![]() $\lambda , \lambda '$
satisfy the assumptions of the theorem. Thanks to Lemma 4.6, we must show that
$\lambda , \lambda '$
satisfy the assumptions of the theorem. Thanks to Lemma 4.6, we must show that
![]() $\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
for all i is equivalent to the condition on
$\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
for all i is equivalent to the condition on
![]() $\lambda _0, \lambda _0^{\prime }$
.
$\lambda _0, \lambda _0^{\prime }$
.
Thanks to (2.7), we have
![]() $z_i^{(n)} = \omega (d^{(n)} p_j) + \omega (q_i^n)$
. Since
$z_i^{(n)} = \omega (d^{(n)} p_j) + \omega (q_i^n)$
. Since
![]() $q_i^n \in S(\mathfrak {g}_n^{\ge 1})$
, it follows from (2.8) that
$q_i^n \in S(\mathfrak {g}_n^{\ge 1})$
, it follows from (2.8) that
![]() $\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
if and only if
$\chi _\lambda (z_i^{(n)}) = \chi _{\lambda '}(z_i^{(n)})$
if and only if
![]() $\chi _\lambda \circ \omega \circ d^{(n)}(p_j) = \chi _{\lambda '} \circ \omega \circ d^{(n)}(p_j)$
for all
$\chi _\lambda \circ \omega \circ d^{(n)}(p_j) = \chi _{\lambda '} \circ \omega \circ d^{(n)}(p_j)$
for all
![]() $i=1,...,r$
. We note that this second equality is well-defined because
$i=1,...,r$
. We note that this second equality is well-defined because
![]() $d^{(n)}$
sends
$d^{(n)}$
sends
![]() $\mathfrak {h}$
-invariants to
$\mathfrak {h}$
-invariants to
![]() $\mathfrak {h}$
-invariants (Lemma 2.2), and
$\mathfrak {h}$
-invariants (Lemma 2.2), and
![]() $\omega $
is
$\omega $
is
![]() $\mathfrak {h}_n$
-equivariant, and
$\mathfrak {h}_n$
-equivariant, and
![]() $\chi _\lambda $
coincides with the composition (4.2).
$\chi _\lambda $
coincides with the composition (4.2).
Since
![]() $\mu := \lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
, we can apply Lemma 4.5 to see that the central characters coincide if and only if
$\mu := \lambda _{\ge 1} = \lambda ^{\prime }_{\ge 1}$
, we can apply Lemma 4.5 to see that the central characters coincide if and only if
![]() $\eta _{\mu }(\lambda _0) = \eta _{\mu }(\lambda _0^{\prime })$
. Let
$\eta _{\mu }(\lambda _0) = \eta _{\mu }(\lambda _0^{\prime })$
. Let
![]() $\pi : \mathfrak {h}^{*} \rightarrow \mathfrak {h}^{*}/W \cong \mathbb {C}^r$
be the quotient map. It follows from the Chevalley restriction theorem [Reference Chriss and GinzburgCGi10, Theorem 3.1.38] that we can write this in coordinates as
$\pi : \mathfrak {h}^{*} \rightarrow \mathfrak {h}^{*}/W \cong \mathbb {C}^r$
be the quotient map. It follows from the Chevalley restriction theorem [Reference Chriss and GinzburgCGi10, Theorem 3.1.38] that we can write this in coordinates as
![]() $\pi (\nu ) = (p_1|_{\mathfrak {h}^{*}}(\nu ),...,p_r|_{\mathfrak {h}^{*}}(\nu ))$
. Now, it is easy to see by a direct comparison of the two definitions that
$\pi (\nu ) = (p_1|_{\mathfrak {h}^{*}}(\nu ),...,p_r|_{\mathfrak {h}^{*}}(\nu ))$
. Now, it is easy to see by a direct comparison of the two definitions that
![]() $\eta _{\mu }(\lambda _0)$
coincides with the differential
$\eta _{\mu }(\lambda _0)$
coincides with the differential
![]() $d_{\lambda _n}\pi (\lambda _0)$
of the quotient map
$d_{\lambda _n}\pi (\lambda _0)$
of the quotient map
![]() $\pi $
.
$\pi $
.
By [Reference ChaffeCh23, Lemma 4.6(e)], we see that
![]() $\ker \eta _\mu = \ker d_{\lambda _n} \pi = \mathbb {C}\Phi _{\lambda _n}$
. This implies that
$\ker \eta _\mu = \ker d_{\lambda _n} \pi = \mathbb {C}\Phi _{\lambda _n}$
. This implies that
![]() $\eta _{\mu }(\lambda _0) = \eta _{\mu }(\lambda _0^{\prime })$
if and only if
$\eta _{\mu }(\lambda _0) = \eta _{\mu }(\lambda _0^{\prime })$
if and only if
![]() $\lambda _0 - \lambda _0^{\prime } \in \mathbb {C} \Phi _{\mu _n}$
(this is where we use the fact that the centralizer in a standard Levi subalgebra). This completes the proof.
$\lambda _0 - \lambda _0^{\prime } \in \mathbb {C} \Phi _{\mu _n}$
(this is where we use the fact that the centralizer in a standard Levi subalgebra). This completes the proof.
4.2 Exactness of the invariants functor
In this section, we fix a standard parabolic subalgebra
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathfrak {g}$
, so that our fixed choice of positive root spaces are contained in
$\mathfrak {g}$
, so that our fixed choice of positive root spaces are contained in
![]() $\mathfrak {p}$
. Pick a Levi decomposition
$\mathfrak {p}$
. Pick a Levi decomposition
![]() $\mathfrak {p} = \mathfrak {l} \oplus \mathfrak {r}$
. The main result of this section is that
$\mathfrak {p} = \mathfrak {l} \oplus \mathfrak {r}$
. The main result of this section is that
![]() $(\bullet)^{{\mathfrak {r}}_n}$
is exact on
$(\bullet)^{{\mathfrak {r}}_n}$
is exact on
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
provided
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
provided
![]() $\mathfrak {g}^{\mu _n} = {\mathfrak {l}}$
. First, we need the following lemma.
$\mathfrak {g}^{\mu _n} = {\mathfrak {l}}$
. First, we need the following lemma.
Proposition 4.7 Let
![]() $M \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
be an indecomposable module, and let
$M \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
be an indecomposable module, and let
![]() $\Xi _M \in \mathfrak {h}^{*} / \mathbb {C} \Phi _{\mu _n}$
be the coset determined by M in Corollary 4.3. If
$\Xi _M \in \mathfrak {h}^{*} / \mathbb {C} \Phi _{\mu _n}$
be the coset determined by M in Corollary 4.3. If
![]() ${\mathfrak {l}} = \mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, then
${\mathfrak {l}} = \mathfrak {g}^{\mu _n}$
is a standard Levi subalgebra, then
Proof Since M is indecomposable and admits a highest weight subquotient of weight
![]() $\lambda $
, we have
$\lambda $
, we have
![]() $\lambda _n = \mu _n$
. Since
$\lambda _n = \mu _n$
. Since
![]() $\mathfrak {g}^{\mu _n}$
is the Levi factor of a standard parabolic, we have
$\mathfrak {g}^{\mu _n}$
is the Levi factor of a standard parabolic, we have
![]() $\mathfrak {r} = \operatorname {span}\{e_{\alpha }: \alpha \in \Phi ^+ \backslash \Phi _{\lambda _n}\}$
. By Lemma 3.3, we have a finite filtration
$\mathfrak {r} = \operatorname {span}\{e_{\alpha }: \alpha \in \Phi ^+ \backslash \Phi _{\lambda _n}\}$
. By Lemma 3.3, we have a finite filtration
![]() $0 \subseteq M_1 \subseteq \dots \subseteq M_k = M$
such that
$0 \subseteq M_1 \subseteq \dots \subseteq M_k = M$
such that
![]() $M_i / M_{i-1}$
has highest weight
$M_i / M_{i-1}$
has highest weight
![]() $\lambda ^{(i)} \in \mathfrak {h}_n^{*}$
. By (3.3), the weights of M lie in the set
$\lambda ^{(i)} \in \mathfrak {h}_n^{*}$
. By (3.3), the weights of M lie in the set
![]() $\bigcup _{i=1}^k \{\lambda ^{(i)}_0 - \sum _{\beta \in \Phi ^+} k_\beta \beta \mid k_\beta \in \mathbb {Z}_{\ge 0}\}$
. Furthermore, by Corollary 4.3, there is an element
$\bigcup _{i=1}^k \{\lambda ^{(i)}_0 - \sum _{\beta \in \Phi ^+} k_\beta \beta \mid k_\beta \in \mathbb {Z}_{\ge 0}\}$
. Furthermore, by Corollary 4.3, there is an element
![]() $\Xi _M \in \mathfrak {h}^{*}/ \mathbb {C} \Phi _{\mu _n}$
such that
$\Xi _M \in \mathfrak {h}^{*}/ \mathbb {C} \Phi _{\mu _n}$
such that
![]() $\lambda _0^{(i)} + \mathbb {C} \Phi _{\mu _n} = \Xi _M$
for all i. It follows that the weights of M actually lie in the set
$\lambda _0^{(i)} + \mathbb {C} \Phi _{\mu _n} = \Xi _M$
for all i. It follows that the weights of M actually lie in the set
![]() $\lambda ^{(i)} + \mathbb {C} \Phi _{\mu _n} - \sum _{\beta \in \Phi ^+} \mathbb {Z}_{\ge 0} \beta $
, for any choice of i.
$\lambda ^{(i)} + \mathbb {C} \Phi _{\mu _n} - \sum _{\beta \in \Phi ^+} \mathbb {Z}_{\ge 0} \beta $
, for any choice of i.
In particular if
![]() $\nu \in \mathfrak {h}^{*}$
satisfies
$\nu \in \mathfrak {h}^{*}$
satisfies
![]() $\nu \in \lambda _0 + \Phi _{\lambda _n}$
, then
$\nu \in \lambda _0 + \Phi _{\lambda _n}$
, then
![]() $\nu + \alpha $
does not lie in
$\nu + \alpha $
does not lie in
![]() $\lambda ^{(i)}_0 - \sum _{\beta \in \Phi ^+} \mathbb {Z}_{\ge 0} \beta $
for any
$\lambda ^{(i)}_0 - \sum _{\beta \in \Phi ^+} \mathbb {Z}_{\ge 0} \beta $
for any
![]() $\alpha \in \Phi ^+ \setminus \Phi _{\lambda _n}$
and for any i. Therefore,
$\alpha \in \Phi ^+ \setminus \Phi _{\lambda _n}$
and for any i. Therefore,
![]() ${\mathfrak {r}}_n \cdot M^{\nu } = 0$
.
${\mathfrak {r}}_n \cdot M^{\nu } = 0$
.
Conversely, suppose
![]() $v\in M^{\mathfrak {r}_n}$
is of weight
$v\in M^{\mathfrak {r}_n}$
is of weight
![]() $\nu \in \mathfrak {h}^{*}$
. Since
$\nu \in \mathfrak {h}^{*}$
. Since
![]() $\mathfrak {h}_n$
acts locally finitely and preserves weight spaces, we can find a common eigenvector for
$\mathfrak {h}_n$
acts locally finitely and preserves weight spaces, we can find a common eigenvector for
![]() $\mathfrak {h}_n$
of weight
$\mathfrak {h}_n$
of weight
![]() $\nu $
in
$\nu $
in
![]() $U(\mathfrak {h}_n)\cdot v$
. Suppose the eigenvalue is
$U(\mathfrak {h}_n)\cdot v$
. Suppose the eigenvalue is
![]() $\lambda ' \in \mathfrak {h}_n^{*}$
(by assumption
$\lambda ' \in \mathfrak {h}_n^{*}$
(by assumption
![]() $\lambda ^{\prime }_0 = \nu $
). Then a quotient of
$\lambda ^{\prime }_0 = \nu $
). Then a quotient of
![]() $M_{\lambda '}$
occurs as a submodule of M. All highest weight modules are indecomposable (they admit unique maximal submodules), and this forces the generalized central character of M to be
$M_{\lambda '}$
occurs as a submodule of M. All highest weight modules are indecomposable (they admit unique maximal submodules), and this forces the generalized central character of M to be
![]() $\chi _{\lambda '}$
. Now, Theorem 4.2 implies that
$\chi _{\lambda '}$
. Now, Theorem 4.2 implies that
![]() $\nu \in \lambda _0^{\prime } + \mathbb {C}\Phi _{\mu _n}$
. By Corollary 4.3, we see that
$\nu \in \lambda _0^{\prime } + \mathbb {C}\Phi _{\mu _n}$
. By Corollary 4.3, we see that
![]() $\lambda _0^{\prime }$
and
$\lambda _0^{\prime }$
and
![]() $\lambda _0$
lie in the same coset of
$\lambda _0$
lie in the same coset of
![]() $\mathfrak {h}^{*}$
modulo
$\mathfrak {h}^{*}$
modulo
![]() $\mathbb {C}\Phi _{\mu _n}$
, and so
$\mathbb {C}\Phi _{\mu _n}$
, and so
![]() $\nu \in \lambda _0 + \mathbb {C}\Phi _{\mu _n}$
.
$\nu \in \lambda _0 + \mathbb {C}\Phi _{\mu _n}$
.
Corollary 4.8 Suppose that
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
such that
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
such that
![]() $\mathfrak {g}^{\mu _n} = \mathfrak {l}$
is a standard Levi subalgebra. Then the functor
$\mathfrak {g}^{\mu _n} = \mathfrak {l}$
is a standard Levi subalgebra. Then the functor
![]() $(\bullet)^{\mathfrak {r}_n} : {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n) \to {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n^{\mu _n})$
is exact.
$(\bullet)^{\mathfrak {r}_n} : {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n) \to {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n^{\mu _n})$
is exact.
Proof It suffices to take a surjective morphism
![]() $M \to N$
in
$M \to N$
in
![]() ${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
, and show that the restriction
${\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
, and show that the restriction
![]() $M^{\mathfrak {r}_n} \rightarrow N^{\mathfrak {r}_n}$
is surjective. Without loss of generality, we can assume that
$M^{\mathfrak {r}_n} \rightarrow N^{\mathfrak {r}_n}$
is surjective. Without loss of generality, we can assume that
![]() $M, N$
are indecomposable. The existence of a nonzero map
$M, N$
are indecomposable. The existence of a nonzero map
![]() $M \to N$
forces
$M \to N$
forces
![]() $\Xi _M = \Xi _N$
. Since objects of
$\Xi _M = \Xi _N$
. Since objects of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
are
${\mathcal {O}}(\mathfrak {g}_n)$
are
![]() $\mathfrak {h}$
-semisimple, it follows that
$\mathfrak {h}$
-semisimple, it follows that
![]() $M \to N$
is surjective on
$M \to N$
is surjective on
![]() $\mathfrak {h}$
-weight spaces, and now the result follows immediately from Proposition 4.7.
$\mathfrak {h}$
-weight spaces, and now the result follows immediately from Proposition 4.7.
Proof of Theorem 4.1
We let
![]() $\varphi _M$
and
$\varphi _M$
and
![]() $\psi _N$
be the adjunction morphisms from (4.1).
$\psi _N$
be the adjunction morphisms from (4.1).
Note that
![]() $\operatorname {Ind}$
is an exact functor because
$\operatorname {Ind}$
is an exact functor because
![]() $U(\mathfrak {g}_n)$
is free over
$U(\mathfrak {g}_n)$
is free over
![]() $U(\mathfrak {p}_n)$
, thanks to the PBW theorem. Furthermore,
$U(\mathfrak {p}_n)$
, thanks to the PBW theorem. Furthermore,
![]() $(\bullet)^{{\mathfrak {r}}_n}$
is exact by Corollary 4.8. If we can check that
$(\bullet)^{{\mathfrak {r}}_n}$
is exact by Corollary 4.8. If we can check that
![]() $\varphi _M$
and
$\varphi _M$
and
![]() $\psi _N$
are isomorphisms on highest weight modules, then a standard argument using the length of a highest weight filtration (Lemma 3.3) can be used to conclude that
$\psi _N$
are isomorphisms on highest weight modules, then a standard argument using the length of a highest weight filtration (Lemma 3.3) can be used to conclude that
![]() $\varphi _M$
and
$\varphi _M$
and
![]() $\psi _N$
are isomorphisms for all
$\psi _N$
are isomorphisms for all
![]() $M \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
and all
$M \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
and all
![]() $N \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n^{\mu _n})$
$N \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n^{\mu _n})$
The map
![]() $\psi _M$
is an isomorphism for highest weight modules M, thanks to Proposition 4.7.
$\psi _M$
is an isomorphism for highest weight modules M, thanks to Proposition 4.7.
Now, suppose that
![]() $N \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
is a highest weight module with highest weight generator v. Since
$N \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
is a highest weight module with highest weight generator v. Since
![]() ${\mathfrak {r}}_n \cdot v = 0$
, it follows that
${\mathfrak {r}}_n \cdot v = 0$
, it follows that
![]() $1\otimes v$
lies in the image of
$1\otimes v$
lies in the image of
![]() $\varphi _N$
and so
$\varphi _N$
and so
![]() $\varphi _N$
is surjective. To prove injectivity, let
$\varphi _N$
is surjective. To prove injectivity, let
![]() $K = \ker (\varphi _N)$
and consider the short exact sequence
$K = \ker (\varphi _N)$
and consider the short exact sequence
![]() $K \to \operatorname {Ind}(N^{{\mathfrak {r}}_n}) \to N$
. By Corollary 4.8, we have another short exact sequence
$K \to \operatorname {Ind}(N^{{\mathfrak {r}}_n}) \to N$
. By Corollary 4.8, we have another short exact sequence
![]() $K^{\mathfrak {r}_n} \to \operatorname {Ind}(N^{{\mathfrak {r}}_n})^{{\mathfrak {r}}_n} \to N^{{\mathfrak {r}}_n}$
.
$K^{\mathfrak {r}_n} \to \operatorname {Ind}(N^{{\mathfrak {r}}_n})^{{\mathfrak {r}}_n} \to N^{{\mathfrak {r}}_n}$
.
Now, set
![]() $M = N^{{\mathfrak {r}}_n}$
, which is a highest weight
$M = N^{{\mathfrak {r}}_n}$
, which is a highest weight
![]() $\mathfrak {g}^{\mu _n}_n$
-module generated by v. The map
$\mathfrak {g}^{\mu _n}_n$
-module generated by v. The map
![]() $\operatorname {Ind}(M)^{{\mathfrak {r}}_n} \to M$
is
$\operatorname {Ind}(M)^{{\mathfrak {r}}_n} \to M$
is
![]() $U(\mathfrak {g}_n)$
-equivariant map uniquely determined by
$U(\mathfrak {g}_n)$
-equivariant map uniquely determined by
![]() $1\otimes m \mapsto m$
. Therefore, it is the left inverse of
$1\otimes m \mapsto m$
. Therefore, it is the left inverse of
![]() $\psi _M$
, which we have already shown to be bijective. It follows that
$\psi _M$
, which we have already shown to be bijective. It follows that
![]() $K^{{\mathfrak {r}}_n} = 0$
, but since every nonzero object in
$K^{{\mathfrak {r}}_n} = 0$
, but since every nonzero object in
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
admits a nonzero highest weight vector, it follows that
${\mathcal {O}}(\mathfrak {g}_n)$
admits a nonzero highest weight vector, it follows that
![]() $K = 0$
and so
$K = 0$
and so
![]() $\varphi _N$
is an isomorphism for highest weight N.
$\varphi _N$
is an isomorphism for highest weight N.
This concludes the proof.
5 Twisting functors
5.1 Definition of twisting functors
Now, we proceed to proving Theorem 1.3, extending the results of the first author [Reference ChaffeCh23, Section 5]. Throughout this section, we fix a simple root
![]() $\alpha \in \Delta $
and make the notation
$\alpha \in \Delta $
and make the notation
![]() $U := U(\mathfrak {g}_n)$
for the sake of brevity.
$U := U(\mathfrak {g}_n)$
for the sake of brevity.
Recall that a right Ore set S in a non-commutative ring R is a multiplicatively closed set of elements such that for all
![]() $r\in R$
and
$r\in R$
and
![]() $s\in S$
, there exist
$s\in S$
, there exist
![]() $r' \in R$
and
$r' \in R$
and
![]() $s' \in S$
such that
$s' \in S$
such that
![]() $rs' = sr'$
. A left Ore set is defined dually. In order for R to admit a right ring of quotients with respect to S, it is necessary that S is a right Ore set. When R has no zero divisors, the condition is also sufficient, and when S is both a right and left Ore set, the left and right fraction fields are isomorphic (see [Reference McConnell and RobsonMR01, Section 2.1] for a survey of these facts).
$rs' = sr'$
. A left Ore set is defined dually. In order for R to admit a right ring of quotients with respect to S, it is necessary that S is a right Ore set. When R has no zero divisors, the condition is also sufficient, and when S is both a right and left Ore set, the left and right fraction fields are isomorphic (see [Reference McConnell and RobsonMR01, Section 2.1] for a survey of these facts).
Also recall the notation
![]() $e_{\alpha , i}, h_{\alpha , i}, h_{\alpha , i}$
from (2.2). Let
$e_{\alpha , i}, h_{\alpha , i}, h_{\alpha , i}$
from (2.2). Let
![]() $F_{\alpha }$
be the multiplicative set generated by
$F_{\alpha }$
be the multiplicative set generated by
![]() $\{f_{\alpha ,0},...,f_{\alpha , n}\}$
, and note that these elements commute among themselves. The proof of the following result is almost identical to [Reference ChaffeCh23, Lemma 5.1].
$\{f_{\alpha ,0},...,f_{\alpha , n}\}$
, and note that these elements commute among themselves. The proof of the following result is almost identical to [Reference ChaffeCh23, Lemma 5.1].
Lemma 5.1
![]() $F_{\alpha }$
is both a left and right Ore set in U.
$F_{\alpha }$
is both a left and right Ore set in U.
We now wish to explicitly construct the localization U with respect to
![]() $F_{\alpha }$
. It certainly exists, by our previous remarks. Consider the U-algebra
$F_{\alpha }$
. It certainly exists, by our previous remarks. Consider the U-algebra
![]() $U_{\alpha } := U[ F_{\alpha }^{-1}]$
, which is freely generated by symbols
$U_{\alpha } := U[ F_{\alpha }^{-1}]$
, which is freely generated by symbols
![]() $\{f_{\alpha , i}^{-1} \mid i=0,1,...,n\}$
, subject to the relations
$\{f_{\alpha , i}^{-1} \mid i=0,1,...,n\}$
, subject to the relations
![]() $f_{\alpha , i} f_{\alpha ,i}^{-1} = 1$
.
$f_{\alpha , i} f_{\alpha ,i}^{-1} = 1$
.
We introduce some notation to describe a basis for
![]() $U_{\alpha }$
. If
$U_{\alpha }$
. If
 $$ \begin{align} \begin{array}{l} k : \Phi^+ \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0},\\ l : \Delta \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0},\\ m : \Phi^+ \setminus \{\alpha\} \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0} \end{array} \end{align} $$
$$ \begin{align} \begin{array}{l} k : \Phi^+ \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0},\\ l : \Delta \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0},\\ m : \Phi^+ \setminus \{\alpha\} \times \{0,1,...,n\} \to \mathbb{Z}_{\ge 0} \end{array} \end{align} $$
are arbitrary maps of sets, then we let
 $$ \begin{align} v(k,l,m) = \Big(\prod_{i=0}^n \prod_{\beta \in \Phi^+} e_{\beta, i}^{k_{\beta, i}}) \Big(\prod_{i=0}^n \prod_{\beta \in \Delta} h_{\beta, i}^{l_{\beta, i}}) \Big(\prod_{i=0}^n \prod_{\beta \in \Phi^+\setminus \{\alpha\}} f_{\beta, i}^{m_{\beta, i}}\Big) \in U, \end{align} $$
$$ \begin{align} v(k,l,m) = \Big(\prod_{i=0}^n \prod_{\beta \in \Phi^+} e_{\beta, i}^{k_{\beta, i}}) \Big(\prod_{i=0}^n \prod_{\beta \in \Delta} h_{\beta, i}^{l_{\beta, i}}) \Big(\prod_{i=0}^n \prod_{\beta \in \Phi^+\setminus \{\alpha\}} f_{\beta, i}^{m_{\beta, i}}\Big) \in U, \end{align} $$
where the product is taken with respect to some fixed choice of ordering on the basis of
![]() $\mathfrak {g}$
. More succinctly, these elements are precisely the PBW monomials in U which have no factor in
$\mathfrak {g}$
. More succinctly, these elements are precisely the PBW monomials in U which have no factor in
![]() $F_{\alpha }$
.
$F_{\alpha }$
.
Lemma 5.2
-
(1)
 $U_{\alpha }$
is the (left and right) localization of U at the Ore set
$U_{\alpha }$
is the (left and right) localization of U at the Ore set
 $F_{\alpha }$
.
$F_{\alpha }$
. -
(2) A basis for
 $U_{\alpha }$
is given by the elements
$U_{\alpha }$
is given by the elements
 $f_{\alpha , 0}^{i_0} \cdots f_{\alpha , n}^{i_n} v(k,l,m)$
where
$f_{\alpha , 0}^{i_0} \cdots f_{\alpha , n}^{i_n} v(k,l,m)$
where
 $i_j \in \mathbb {Z}$
and
$i_j \in \mathbb {Z}$
and
 $k,l,m$
are as in (5.1).
$k,l,m$
are as in (5.1). -
(3) A basis for
 $U_{\alpha }$
is given by the elements
$U_{\alpha }$
is given by the elements
 $v(k,l,m)f_{\alpha , 0}^{i_0} \cdots f_{\alpha , n}^{i_n}$
where
$v(k,l,m)f_{\alpha , 0}^{i_0} \cdots f_{\alpha , n}^{i_n}$
where
 $i_j \in \mathbb {Z}$
and
$i_j \in \mathbb {Z}$
and
 $k,l,m$
are as in (5.1).
$k,l,m$
are as in (5.1).
Proof
![]() $U_{\alpha }$
satisfies the universal property of the localization by construction, and so it is isomorphic to both the left and right localization, thanks to [Reference McConnell and RobsonMR01, Corollary 2.1.4]. This proves (1), and also implies that U embeds inside
$U_{\alpha }$
satisfies the universal property of the localization by construction, and so it is isomorphic to both the left and right localization, thanks to [Reference McConnell and RobsonMR01, Corollary 2.1.4]. This proves (1), and also implies that U embeds inside
![]() $U_{\alpha }$
, and
$U_{\alpha }$
, and
![]() $U_{\alpha }$
is an integral domain.
$U_{\alpha }$
is an integral domain.
Note that
![]() $U_{\alpha }$
is spanned by unordered monomials in
$U_{\alpha }$
is spanned by unordered monomials in
![]() $\mathfrak {g}_n$
and
$\mathfrak {g}_n$
and
![]() $F_{\alpha }^{-1}$
. Using the left Ore condition, we can rewrite any such monomial as a span of monomials of the form described in (2). Furthermore, if there is a linear dependence between the latter monomials, we can left multiply by appropriate elements of
$F_{\alpha }^{-1}$
. Using the left Ore condition, we can rewrite any such monomial as a span of monomials of the form described in (2). Furthermore, if there is a linear dependence between the latter monomials, we can left multiply by appropriate elements of
![]() $F_{\alpha }$
to obtain a linear dependence between PBW monomials in U, which must be zero. This proves (2), and (3) follows by a symmetrical argument.
$F_{\alpha }$
to obtain a linear dependence between PBW monomials in U, which must be zero. This proves (2), and (3) follows by a symmetrical argument.
We will need more precise relations between generators of
![]() $U_{\alpha }$
.
$U_{\alpha }$
.
Lemma 5.3 For any
![]() $i, j \in \mathbb {Z}$
, the following relations hold in
$i, j \in \mathbb {Z}$
, the following relations hold in
![]() $U_{\alpha }$
, for any
$U_{\alpha }$
, for any
![]() $h \in \mathfrak {h}$
and any
$h \in \mathfrak {h}$
and any
![]() $\beta \in \Phi ^+ \setminus \{\alpha \}$
:
$\beta \in \Phi ^+ \setminus \{\alpha \}$
:
for some
![]() $a,b,c \in \mathbb {C}$
. We adopt the convention
$a,b,c \in \mathbb {C}$
. We adopt the convention
![]() $e_{\gamma , i} = 0$
if
$e_{\gamma , i} = 0$
if
![]() $\gamma \notin \Phi $
or if
$\gamma \notin \Phi $
or if
![]() $i> n$
.
$i> n$
.
Proof These can be verified by multiplying by powers of
![]() $f_{\alpha , j}$
to obtain an expression which holds in U. We show the calculation for (5.3); the other relations are proved similarly. Using the relations in U, we have
$f_{\alpha , j}$
to obtain an expression which holds in U. We show the calculation for (5.3); the other relations are proved similarly. Using the relations in U, we have
We then multiply on the left by
![]() $f_{\alpha , j}^{-3}$
and on the right by
$f_{\alpha , j}^{-3}$
and on the right by
![]() $f_{\alpha , j}^{-1}$
to obtain (5.3).
$f_{\alpha , j}^{-1}$
to obtain (5.3).
Let
![]() $V_{\alpha } \subseteq U_{\alpha }$
be the span of the monomials appearing in Lemma 5.2(2) such that
$V_{\alpha } \subseteq U_{\alpha }$
be the span of the monomials appearing in Lemma 5.2(2) such that
![]() $i_j \ge 0$
for some
$i_j \ge 0$
for some
![]() $j = 0,...,n$
. Using an argument identical to the one used in the second half of the proof of [Reference ChaffeCh23, Lemma 5.3], we see that
$j = 0,...,n$
. Using an argument identical to the one used in the second half of the proof of [Reference ChaffeCh23, Lemma 5.3], we see that
![]() $V_{\alpha }$
can be defined symmetrically as the span of the monomials appearing in Lemma 5.2(3), subject to the condition
$V_{\alpha }$
can be defined symmetrically as the span of the monomials appearing in Lemma 5.2(3), subject to the condition
![]() $i_j \ge 0$
for some j. Using an argument identical to loc. cit., once again we obtain the following.
$i_j \ge 0$
for some j. Using an argument identical to loc. cit., once again we obtain the following.
Lemma 5.4
![]() $V_{\alpha }$
is a U–U-sub-bimodule of
$V_{\alpha }$
is a U–U-sub-bimodule of
![]() $U_{\alpha }$
.
$U_{\alpha }$
.
We now consider the U–U-bimodule
By Lemma 5.2, we see that
![]() $S_{\alpha }$
has a basis given by
$S_{\alpha }$
has a basis given by
and another basis given by
As a slight abuse of notation, we denote an element of
![]() $U_{\alpha }$
and its coset in
$U_{\alpha }$
and its coset in
![]() $S_{\alpha }$
by the same symbol.
$S_{\alpha }$
by the same symbol.
Now, we pick a special automorphism of
![]() $\mathfrak {g}$
. The simple root
$\mathfrak {g}$
. The simple root
![]() $\alpha $
which we have fixed throughout this section gives rise to a reflection
$\alpha $
which we have fixed throughout this section gives rise to a reflection
![]() $s_{\alpha } \in W = N_G(\mathfrak {h}) / \mathfrak {h}$
. We lift
$s_{\alpha } \in W = N_G(\mathfrak {h}) / \mathfrak {h}$
. We lift
![]() $s_{\alpha }$
arbitrarily to an element of
$s_{\alpha }$
arbitrarily to an element of
![]() $N_G(\mathfrak {h})$
, which defines an automorphism of
$N_G(\mathfrak {h})$
, which defines an automorphism of
![]() $\mathfrak {g}$
via the adjoint representation. We denote this automorphism by
$\mathfrak {g}$
via the adjoint representation. We denote this automorphism by
![]() $\phi _{\alpha }$
.
$\phi _{\alpha }$
.
Note that
![]() $\phi _{\alpha }$
acts on the root spaces as
$\phi _{\alpha }$
acts on the root spaces as
![]() $s_{\alpha }$
, i.e., it sends
$s_{\alpha }$
, i.e., it sends
![]() $\mathfrak {g}_\beta $
to
$\mathfrak {g}_\beta $
to
![]() $\mathfrak {g}_{s_{\alpha }(\beta )}$
and preserves
$\mathfrak {g}_{s_{\alpha }(\beta )}$
and preserves
![]() $\mathfrak {h}$
. Furthermore, after rescaling
$\mathfrak {h}$
. Furthermore, after rescaling
![]() $e_{\alpha }$
and
$e_{\alpha }$
and
![]() $f_{\alpha }$
if necessary, we may assume that
$f_{\alpha }$
if necessary, we may assume that
 $$ \begin{align*} \phi_{\alpha}(e_{\alpha}) &= f_{\alpha},\\ \phi_{\alpha}(f_{\alpha}) &= e_{\alpha}. \end{align*} $$
$$ \begin{align*} \phi_{\alpha}(e_{\alpha}) &= f_{\alpha},\\ \phi_{\alpha}(f_{\alpha}) &= e_{\alpha}. \end{align*} $$
We extend
![]() $\phi _{\alpha }$
to an automorphism of
$\phi _{\alpha }$
to an automorphism of
![]() $\mathfrak {g}_n$
by the rule
$\mathfrak {g}_n$
by the rule
![]() $\phi _{\alpha }(x_i) = \phi _{\alpha }(x)_i$
for all
$\phi _{\alpha }(x_i) = \phi _{\alpha }(x)_i$
for all
![]() $x \in \mathfrak {g}$
.
$x \in \mathfrak {g}$
.
If M is a left U-module, we denote by
![]() $\phi _{\alpha }(M)$
the module obtained by twisting the left action on M by
$\phi _{\alpha }(M)$
the module obtained by twisting the left action on M by
![]() $\phi _{\alpha }$
and write
$\phi _{\alpha }$
and write
![]() $\cdot _{\alpha }$
for this action. More precisely, if
$\cdot _{\alpha }$
for this action. More precisely, if
![]() $m \in M$
and
$m \in M$
and
![]() $u \in U$
, then
$u \in U$
, then
![]() $u \cdot _{\alpha } m := \phi _{\alpha }(u) \cdot m$
. Similarly, we can similarly twist the action by
$u \cdot _{\alpha } m := \phi _{\alpha }(u) \cdot m$
. Similarly, we can similarly twist the action by
![]() $\phi _{\alpha }^{-1}$
, and use notation
$\phi _{\alpha }^{-1}$
, and use notation
![]() $\cdot _{\alpha ^{-1}}$
in this case.
$\cdot _{\alpha ^{-1}}$
in this case.
Let
![]() $\mathcal {C}$
be the full subcategory of U-mod whose objects are the
$\mathcal {C}$
be the full subcategory of U-mod whose objects are the
![]() $\mathfrak {h}$
-semisimple modules. The proof of the next result is the same as [Reference ChaffeCh23, Lemma 5.9].
$\mathfrak {h}$
-semisimple modules. The proof of the next result is the same as [Reference ChaffeCh23, Lemma 5.9].
Lemma 5.5
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
is a Serre subcategory of the category of
${\mathcal {O}}(\mathfrak {g}_n)$
is a Serre subcategory of the category of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
We define a functor
![]() $\mathcal {H}$
from U-mod to
$\mathcal {H}$
from U-mod to
![]() $\mathcal {C}$
by letting
$\mathcal {C}$
by letting
![]() $\mathcal {H}(M)$
be the sum of the
$\mathcal {H}(M)$
be the sum of the
![]() $\mathfrak {h}$
-weight spaces in M.
$\mathfrak {h}$
-weight spaces in M.
Now, we define two endofunctors of
![]() $\mathcal {C}$
by setting
$\mathcal {C}$
by setting
Note that the action of U on
![]() $G_{\alpha } M$
is given by
$G_{\alpha } M$
is given by
Also, note that if
![]() $M, N \in \mathcal {C}$
and
$M, N \in \mathcal {C}$
and
![]() $\chi \in \operatorname {Hom}_{\mathcal {C}}(M,N)$
, then
$\chi \in \operatorname {Hom}_{\mathcal {C}}(M,N)$
, then
![]() $T_{\alpha }(\chi ): T_{\alpha } M \rightarrow T_{\alpha } N$
and
$T_{\alpha }(\chi ): T_{\alpha } M \rightarrow T_{\alpha } N$
and
![]() $G_{\alpha }(\chi ): G_{\alpha } M \rightarrow G_{\alpha } N$
are given by
$G_{\alpha }(\chi ): G_{\alpha } M \rightarrow G_{\alpha } N$
are given by
 $$ \begin{align*} & T_{\alpha}(\chi)(s \otimes m) = s \otimes \chi(m) \text{ for } s \in S_{\alpha}, \ m \in M,\\ & G_{\alpha}(\chi)(\rho) = \chi \circ \rho \text{ for } \rho \in \operatorname{Hom}_U(S_{\alpha}, \phi_{\alpha}^{-1}(M))). \end{align*} $$
$$ \begin{align*} & T_{\alpha}(\chi)(s \otimes m) = s \otimes \chi(m) \text{ for } s \in S_{\alpha}, \ m \in M,\\ & G_{\alpha}(\chi)(\rho) = \chi \circ \rho \text{ for } \rho \in \operatorname{Hom}_U(S_{\alpha}, \phi_{\alpha}^{-1}(M))). \end{align*} $$
In order to see these functors are well defined, the only nontrivial check is that
![]() $T_{\alpha } M \in \mathcal {C}$
for any
$T_{\alpha } M \in \mathcal {C}$
for any
![]() $M \in \mathcal {C}$
. For
$M \in \mathcal {C}$
. For
![]() $M \in \mathcal {C}$
, we see that
$M \in \mathcal {C}$
, we see that
![]() $T_{\alpha } M$
is spanned by
$T_{\alpha } M$
is spanned by
![]() $\{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes w : i_j> 0, w \in \mathcal {H}(M)\}$
. For
$\{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes w : i_j> 0, w \in \mathcal {H}(M)\}$
. For
![]() $w \in M^{\lambda }$
and
$w \in M^{\lambda }$
and
![]() $h \in \mathfrak {h}$
, we have
$h \in \mathfrak {h}$
, we have
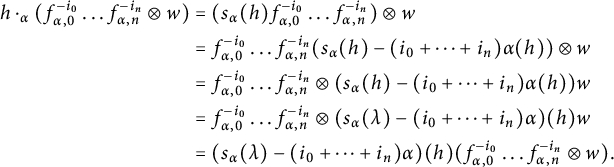 $$ \begin{align*} h \cdot_{\alpha} (f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes w) &= (s_{\alpha}(h)f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n}) \otimes w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} (s_{\alpha}(h) - (i_0 + \dots + i_n) \alpha(h))\otimes w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes (s_{\alpha}(h) - (i_0 + \dots + i_n) \alpha(h)) w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes (s_{\alpha}(\lambda) - (i_0 + \dots + i_n)\alpha)(h) w \\ &= (s_{\alpha}(\lambda) - (i_0 + \dots + i_n)\alpha)(h) (f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes w). \end{align*} $$
$$ \begin{align*} h \cdot_{\alpha} (f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes w) &= (s_{\alpha}(h)f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n}) \otimes w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} (s_{\alpha}(h) - (i_0 + \dots + i_n) \alpha(h))\otimes w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes (s_{\alpha}(h) - (i_0 + \dots + i_n) \alpha(h)) w \\ &= f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes (s_{\alpha}(\lambda) - (i_0 + \dots + i_n)\alpha)(h) w \\ &= (s_{\alpha}(\lambda) - (i_0 + \dots + i_n)\alpha)(h) (f_{\alpha, 0}^{-i_0} \dots f_{\alpha, n}^{-i_n} \otimes w). \end{align*} $$
To summarize, for any
![]() $w \in M$
of weight
$w \in M$
of weight
![]() $\lambda $
, we have
$\lambda $
, we have
In particular,
![]() $T_{\alpha } M$
is spanned by weight vectors, and so is
$T_{\alpha } M$
is spanned by weight vectors, and so is
![]() $\mathfrak {h}$
-semisimple. The following result can be proven by a calculation almost identical to [Reference ChaffeCh23, Lemma 5.4].
$\mathfrak {h}$
-semisimple. The following result can be proven by a calculation almost identical to [Reference ChaffeCh23, Lemma 5.4].
Lemma 5.6 Let
![]() $g \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
. Then g has weight
$g \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
. Then g has weight
![]() $\lambda \in \mathfrak {h}^{*}$
if and only if
$\lambda \in \mathfrak {h}^{*}$
if and only if
![]() $g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n})$
has weight
$g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n})$
has weight
![]() $\lambda + (i_0 + \dots + i_n)\alpha $
in
$\lambda + (i_0 + \dots + i_n)\alpha $
in
![]() $\phi ^{-1}_{\alpha }(M)$
for all
$\phi ^{-1}_{\alpha }(M)$
for all
![]() $i_0,...,i_n \in \mathbb {Z}_{\ge 0}$
, which occurs if and only if this vector has weight
$i_0,...,i_n \in \mathbb {Z}_{\ge 0}$
, which occurs if and only if this vector has weight
![]() $s_{\alpha }(\lambda ) - (i_0 + \dots + i_n) \alpha $
in M.
$s_{\alpha }(\lambda ) - (i_0 + \dots + i_n) \alpha $
in M.
We immediately obtain the following consequence.
Corollary 5.7 Let
![]() $g \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, then g is a weight vector if and only if
$g \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, then g is a weight vector if and only if
![]() $g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n})$
is a weight vector for all
$g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n})$
is a weight vector for all
![]() $i, j \geq 0$
. In particular,
$i, j \geq 0$
. In particular,
![]() $G_{\alpha }(M)$
is the direct sum of such vectors g.
$G_{\alpha }(M)$
is the direct sum of such vectors g.
Lemma 5.8
![]() $T_{\alpha }$
is right exact, and
$T_{\alpha }$
is right exact, and
![]() $G_{\alpha }$
is left exact.
$G_{\alpha }$
is left exact.
Proof For any module
![]() $M \in U\operatorname {-mod}$
,
$M \in U\operatorname {-mod}$
,
and
![]() $(\bullet) \otimes _U M$
is right exact; hence,
$(\bullet) \otimes _U M$
is right exact; hence,
![]() $T_{\alpha }$
is right exact.
$T_{\alpha }$
is right exact.
Similarly,
![]() $G_{\alpha }$
is a composition of two left exact functors,
$G_{\alpha }$
is a composition of two left exact functors,
![]() $\operatorname {Hom}_U(S_{\alpha }, \phi ^{-1}_{\alpha }(\bullet))$
and
$\operatorname {Hom}_U(S_{\alpha }, \phi ^{-1}_{\alpha }(\bullet))$
and
![]() $\mathcal {H}$
; hence, it is also left exact.
$\mathcal {H}$
; hence, it is also left exact.
5.2 Twisting functors between blocks of category
 ${\mathcal {O}}$
${\mathcal {O}}$
Note that the Weyl group action on
![]() $\mathfrak {h}^{*}$
extends naturally to an action on
$\mathfrak {h}^{*}$
extends naturally to an action on
![]() $(\mathfrak {h}_n^{\ge 1})^{*}$
acting diagonally through the identification
$(\mathfrak {h}_n^{\ge 1})^{*}$
acting diagonally through the identification
![]() $(\mathfrak {h}_n^{\ge 1})^{*} = (\mathfrak {h}^{*})^{\oplus n}$
, and this vector space parameterizes the Jordan blocks of
$(\mathfrak {h}_n^{\ge 1})^{*} = (\mathfrak {h}^{*})^{\oplus n}$
, and this vector space parameterizes the Jordan blocks of
![]() ${\mathcal {O}}(\mathfrak {g}_n)$
. Retaining the notation of the previous section, we can now precisely state Theorem 1.3.
${\mathcal {O}}(\mathfrak {g}_n)$
. Retaining the notation of the previous section, we can now precisely state Theorem 1.3.
Theorem 5.9 Let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
be such that
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
be such that
![]() $\mu (h_{\alpha ,n}) \ne 0$
. The functors
$\mu (h_{\alpha ,n}) \ne 0$
. The functors
![]() $T_{\alpha }$
and
$T_{\alpha }$
and
![]() $G_{\alpha }$
from (5.9) restrict to functors
$G_{\alpha }$
from (5.9) restrict to functors
 $$ \begin{align*} T_{\alpha} &: \mathcal{O}^{(\mu)} (\mathfrak{g}_n) \longrightarrow \mathcal{O}^{(s_{\alpha}(\mu))}(\mathfrak{g}_n),\\ G_{\alpha} &: \mathcal{O}^{(s_{\alpha}(\mu))}(\mathfrak{g}_n) \longrightarrow \mathcal{O}^{(\mu)}(\mathfrak{g}_n). \end{align*} $$
$$ \begin{align*} T_{\alpha} &: \mathcal{O}^{(\mu)} (\mathfrak{g}_n) \longrightarrow \mathcal{O}^{(s_{\alpha}(\mu))}(\mathfrak{g}_n),\\ G_{\alpha} &: \mathcal{O}^{(s_{\alpha}(\mu))}(\mathfrak{g}_n) \longrightarrow \mathcal{O}^{(\mu)}(\mathfrak{g}_n). \end{align*} $$
These form a quasi-inverse pair of equivalences.
The proof of Theorem 5.9 will be broken down into a series of lemmas, which we record and prove over the course of this section. To be more precise, the theorem will follow directly from Lemmas 5.10, 5.13, and 5.16–5.18.
For the rest of the section, we keep
![]() $\alpha $
fixed and let
$\alpha $
fixed and let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
be such that
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
be such that
![]() $\mu (h_{\alpha ,n}) \neq 0$
.
$\mu (h_{\alpha ,n}) \neq 0$
.
The next result is the first step in the proof of Theorem 5.9, and is a generalization of [Reference ChaffeCh23, Lemma 5.3]. The proof given here is an alternative, shorter argument.
Lemma 5.10
![]() $T_{\alpha }$
restricts to a functor
$T_{\alpha }$
restricts to a functor
![]() $\mathcal {O}^{(\mu )}(\mathfrak {g}_n) \rightarrow \mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n)$
.
$\mathcal {O}^{(\mu )}(\mathfrak {g}_n) \rightarrow \mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n)$
.
Proof For
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, we let
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, we let
![]() $l(M)$
denote the minimal length of a filtration
$l(M)$
denote the minimal length of a filtration
![]() $0 = M_0 \subseteq M_1 \subseteq \dots \subseteq M_{k-1} \subseteq M_k = M$
such that the sections are highest weight modules (cf. Lemma 3.3). We have an exact sequence
$0 = M_0 \subseteq M_1 \subseteq \dots \subseteq M_{k-1} \subseteq M_k = M$
such that the sections are highest weight modules (cf. Lemma 3.3). We have an exact sequence
and since
![]() $T_{\alpha }$
is right exact, we have an exact sequence
$T_{\alpha }$
is right exact, we have an exact sequence
Using Lemma 5.5 and the fact that
![]() $T_{\alpha } M_1$
is a highest weight module, we can reduce the claim that
$T_{\alpha } M_1$
is a highest weight module, we can reduce the claim that
![]() $T_{\alpha }(M) \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
$T_{\alpha }(M) \in {\mathcal {O}}^{(\mu )}(\mathfrak {g}_n)$
to the case where
![]() $l(M) = 1$
, i.e., M is a highest weight module.
$l(M) = 1$
, i.e., M is a highest weight module.
For the rest of the proof, we fix M highest weight of weight
![]() $\lambda \in \mathfrak {h}_n^{*}$
, and let
$\lambda \in \mathfrak {h}_n^{*}$
, and let
![]() $v \in M$
be a highest weight generator of M. We will show that
$v \in M$
be a highest weight generator of M. We will show that
![]() $f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
is highest weight and generates
$f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
is highest weight and generates
![]() $T_{\alpha } M$
, which will complete the proof of the lemma.
$T_{\alpha } M$
, which will complete the proof of the lemma.
To see that the vector is maximal, use (5.11) to see that
![]() $e_{\alpha , i} f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v \in T_{\alpha } M$
lies in an
$e_{\alpha , i} f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v \in T_{\alpha } M$
lies in an
![]() $\mathfrak {h}$
-eigenspace whose weight is not a weight of
$\mathfrak {h}$
-eigenspace whose weight is not a weight of
![]() $T_{\alpha } M$
(for any
$T_{\alpha } M$
(for any
![]() $i \ge 0$
and
$i \ge 0$
and
![]() $\alpha \in \Phi ^+$
). To see that it is a genuine highest weight vector, one can use (5.4) to show that
$\alpha \in \Phi ^+$
). To see that it is a genuine highest weight vector, one can use (5.4) to show that
![]() $h_i$
acts via
$h_i$
acts via
![]() $s_{\alpha _i}(h_i)$
.
$s_{\alpha _i}(h_i)$
.
To see that
![]() $f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
generates
$f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
generates
![]() $T_{\alpha } M$
, we use the fact that
$T_{\alpha } M$
, we use the fact that
![]() $Uv = M$
and that
$Uv = M$
and that
![]() $S_{\alpha }$
has two bases, (5.7) and (5.8), to check that every element of
$S_{\alpha }$
has two bases, (5.7) and (5.8), to check that every element of
![]() $T_{\alpha } M$
lies in the submodule generated by the set
$T_{\alpha } M$
lies in the submodule generated by the set
![]() $\{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes v \mid i_k> 0\}$
. Let L denote the span of this set. Note that it is an
$\{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes v \mid i_k> 0\}$
. Let L denote the span of this set. Note that it is an
![]() $(\mathfrak {sl}_2)_n$
-module, where
$(\mathfrak {sl}_2)_n$
-module, where
![]() $(\mathfrak {sl}_2)_n$
is the truncated current algebra on
$(\mathfrak {sl}_2)_n$
is the truncated current algebra on
![]() $\mathfrak {sl}_2 = \langle e_{\alpha }, h_{\alpha }, f_{\alpha }\rangle $
. To complete the current proof we show that L is a simple
$\mathfrak {sl}_2 = \langle e_{\alpha }, h_{\alpha }, f_{\alpha }\rangle $
. To complete the current proof we show that L is a simple
![]() $(\mathfrak {sl}_2)_n$
-module.
$(\mathfrak {sl}_2)_n$
-module.
Let
![]() $\mathfrak {t}_n \subseteq (\mathfrak {sl}_2)_n$
denote the span on
$\mathfrak {t}_n \subseteq (\mathfrak {sl}_2)_n$
denote the span on
![]() $h_{\alpha ,0},...,h_{\alpha , n}$
, and let
$h_{\alpha ,0},...,h_{\alpha , n}$
, and let
![]() $\gamma = \lambda |_{\mathfrak {t}_n} \in \mathfrak {t}_n^{*}$
give the action on
$\gamma = \lambda |_{\mathfrak {t}_n} \in \mathfrak {t}_n^{*}$
give the action on
![]() $f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
. If
$f_{\alpha , 0}^{-1} \dots f_{\alpha , n}^{-1} \otimes v$
. If
![]() $M_\gamma $
denotes the Verma module of highest weight
$M_\gamma $
denotes the Verma module of highest weight
![]() $\gamma $
, then there is a nonzero homomorphism
$\gamma $
, then there is a nonzero homomorphism
![]() $M_\gamma \to L$
and the dimensions of the weight spaces are the same. Therefore, it remains to show that the Verma module
$M_\gamma \to L$
and the dimensions of the weight spaces are the same. Therefore, it remains to show that the Verma module
![]() $M_\gamma $
is simple. By (5.4), we see that
$M_\gamma $
is simple. By (5.4), we see that
![]() $\gamma (h_{\alpha , n}) = (s_{\alpha } \lambda )(h_{\alpha , n}) \ne 0$
and so we can apply Theorem 4.1 to see that
$\gamma (h_{\alpha , n}) = (s_{\alpha } \lambda )(h_{\alpha , n}) \ne 0$
and so we can apply Theorem 4.1 to see that
![]() ${\mathcal {O}}^{(\gamma _{\ge 1})}((\mathfrak {sl}_2)_n)$
is equivalent to
${\mathcal {O}}^{(\gamma _{\ge 1})}((\mathfrak {sl}_2)_n)$
is equivalent to
![]() ${\mathcal {O}}^{(\gamma _{\ge 1})}(\mathfrak {t}_n)$
. In the latter category, all highest weight modules are simple, and it follows that
${\mathcal {O}}^{(\gamma _{\ge 1})}(\mathfrak {t}_n)$
. In the latter category, all highest weight modules are simple, and it follows that
![]() $M_\gamma $
is simple, as required. This completes the proof.
$M_\gamma $
is simple, as required. This completes the proof.
Consider the abelian Lie algebra
![]() $\mathfrak {a} = \langle f_{\alpha , 0}, \dots , f_{\alpha , n} \rangle $
contained in
$\mathfrak {a} = \langle f_{\alpha , 0}, \dots , f_{\alpha , n} \rangle $
contained in
![]() $\mathfrak {g}_n$
, and let
$\mathfrak {g}_n$
, and let
![]() $A := \operatorname {span} \{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}: i_0, \dots , i_n> 0 \} \subseteq S_{\alpha }$
, which is a
$A := \operatorname {span} \{f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}: i_0, \dots , i_n> 0 \} \subseteq S_{\alpha }$
, which is a
![]() $U(\mathfrak {a})$
–
$U(\mathfrak {a})$
–
![]() $U(\mathfrak {a})$
-subbimodule of
$U(\mathfrak {a})$
-subbimodule of
![]() $S_{\alpha }$
. Thanks to the description of the two bases (5.7) and (5.8) of
$S_{\alpha }$
. Thanks to the description of the two bases (5.7) and (5.8) of
![]() $S_{\alpha }$
, we have an isomorphism of U–
$S_{\alpha }$
, we have an isomorphism of U–
![]() $U(\mathfrak {a})$
-bimodules
$U(\mathfrak {a})$
-bimodules
and an isomorphism of
![]() $U(\mathfrak {a})$
–U-bimodules
$U(\mathfrak {a})$
–U-bimodules
In particular, for any left U-module M, we have an isomorphism of left
![]() $U(\mathfrak {a})$
-modules
$U(\mathfrak {a})$
-modules
Recall that
![]() $\mu \in \mathfrak {h}_n^{*}$
satisfies
$\mu \in \mathfrak {h}_n^{*}$
satisfies
![]() $\mu (h_{\alpha ,n}) \neq 0$
.
$\mu (h_{\alpha ,n}) \neq 0$
.
Lemma 5.11 [Reference ChaffeCh23, Lemma 5.13]
Let
![]() $M \in \mathcal {O}^{(\mu )}$
. Let
$M \in \mathcal {O}^{(\mu )}$
. Let
![]() $m \in M^\lambda \backslash \{0\}$
for some
$m \in M^\lambda \backslash \{0\}$
for some
![]() $\lambda \in \mathfrak {h}^{*}$
. Then the following are equivalent:
$\lambda \in \mathfrak {h}^{*}$
. Then the following are equivalent:
-
(a) In
 $T_{\alpha } M$
, we have
$T_{\alpha } M$
, we have
 $f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes m = 0$
.
$f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes m = 0$
. -
(b) For any vector space V and
 $U(\mathfrak {a})$
-balanced map
$U(\mathfrak {a})$
-balanced map
 $\varphi : A \times M \rightarrow V$
, we have
$\varphi : A \times M \rightarrow V$
, we have
 $\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}, m) = 0$
.
$\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}, m) = 0$
. -
(c) There exist
 $m_0, \dots , m_n \in M$
such that
$m_0, \dots , m_n \in M$
such that
 $m = f_{\alpha , 0}^{i_0} \cdot m_0 + \dots + f_{\alpha , n}^{i_n} \cdot m_n$
.
$m = f_{\alpha , 0}^{i_0} \cdot m_0 + \dots + f_{\alpha , n}^{i_n} \cdot m_n$
.
The following fact only depends on the existence of inverses for
![]() $f_{\alpha , i}$
in
$f_{\alpha , i}$
in
![]() $S_{\alpha }$
. We omit the proof.
$S_{\alpha }$
. We omit the proof.
Lemma 5.12 [Reference ChaffeCh23, Lemma 5.15]
Let
![]() $M \in U$
-mod. Then any element of
$M \in U$
-mod. Then any element of
![]() $S_{\alpha } \otimes M$
can be written in the form
$S_{\alpha } \otimes M$
can be written in the form
![]() $f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes m$
, for some
$f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes m$
, for some
![]() $i_0, \dots , i_n> 0$
and
$i_0, \dots , i_n> 0$
and
![]() $m \in M$
.
$m \in M$
.
Lemma 5.13 [Reference ChaffeCh23, Lemma 5.7(b)]
For any
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, the map
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, the map
![]() $\psi _M : M \rightarrow G_{\alpha } T_{\alpha } M$
given by
$\psi _M : M \rightarrow G_{\alpha } T_{\alpha } M$
given by
![]() $\psi _M(m)(s) = s \otimes m$
is an isomorphism.
$\psi _M(m)(s) = s \otimes m$
is an isomorphism.
Lemma 5.14 [Reference ChaffeCh23, Lemma 5.16]
Let M be a U-module, and let
![]() $A \subseteq S_{\alpha }$
and
$A \subseteq S_{\alpha }$
and
![]() $\mathfrak {a} \subseteq \mathfrak {g}$
be as in Lemma 5.11. Let
$\mathfrak {a} \subseteq \mathfrak {g}$
be as in Lemma 5.11. Let
![]() $\varphi : A \rightarrow M$
be a
$\varphi : A \rightarrow M$
be a
![]() $U(\mathfrak {a})$
-homomorphism. Then
$U(\mathfrak {a})$
-homomorphism. Then
![]() $\varphi $
extends uniquely to a U-homomorphism
$\varphi $
extends uniquely to a U-homomorphism
![]() $\varphi : S_{\alpha } \rightarrow M$
.
$\varphi : S_{\alpha } \rightarrow M$
.
This next result is a generalization of [Reference ChaffeCh23, Lemma 5.17], but we provide the proof, which is more complicated in the present setting.
Lemma 5.15 Let
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, and let
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, and let
![]() $\mathcal {I}$
be a subset of
$\mathcal {I}$
be a subset of
![]() $\mathbb {Z}^{n+1}$
satisfying:
$\mathbb {Z}^{n+1}$
satisfying:
-
(1)
 $(i_0, \dots , i_n) \in \mathcal {I}$
whenever any
$(i_0, \dots , i_n) \in \mathcal {I}$
whenever any
 $i_k \leq 0$
,
$i_k \leq 0$
, -
(2) If
 $(i_0, \dots , i_n) \in \mathcal {I}$
, then
$(i_0, \dots , i_n) \in \mathcal {I}$
, then
 $(i_0, \dots , i_k-1, \dots , i_n) \in \mathcal {I}$
for any
$(i_0, \dots , i_k-1, \dots , i_n) \in \mathcal {I}$
for any
 $0 \leq k \leq n$
,
$0 \leq k \leq n$
,
and let
![]() $\{m_{i_0, \dots , i_n} \in M : (i_0, \dots , i_n) \in \mathcal {I}\}$
be a collection of elements of M satisfying:
$\{m_{i_0, \dots , i_n} \in M : (i_0, \dots , i_n) \in \mathcal {I}\}$
be a collection of elements of M satisfying:
-
(i)
 $m_{i_0, \dots , i_n} = 0$
whenever any
$m_{i_0, \dots , i_n} = 0$
whenever any
 $i_k \leq 0$
,
$i_k \leq 0$
, -
(ii)
 $e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k-1, \dots , i_n}$
whenever
$e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k-1, \dots , i_n}$
whenever
 $(i_0, \dots , i_n) \in \mathcal {I}.$
$(i_0, \dots , i_n) \in \mathcal {I}.$
Then there exists a
![]() $U(\mathfrak {a})$
-homomorphism
$U(\mathfrak {a})$
-homomorphism
![]() $\varphi : A \rightarrow \phi _{\alpha }^{-1}(M)$
such that
$\varphi : A \rightarrow \phi _{\alpha }^{-1}(M)$
such that
![]() $\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = m_{i_0, \dots , i_n}$
, which, by Lemma 5.14, extends to a U-homomorphism
$\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = m_{i_0, \dots , i_n}$
, which, by Lemma 5.14, extends to a U-homomorphism
![]() $\varphi : S_{\alpha } \rightarrow \phi _{\alpha }^{-1}(M)$
. Moreover, if there exists
$\varphi : S_{\alpha } \rightarrow \phi _{\alpha }^{-1}(M)$
. Moreover, if there exists
![]() $\lambda \in \mathfrak {h}^{*}$
such that the weight of
$\lambda \in \mathfrak {h}^{*}$
such that the weight of
![]() $m_{i_0, \dots , i_n}$
is
$m_{i_0, \dots , i_n}$
is
![]() $\lambda - (i_0 + \dots + i_n)\alpha $
for all
$\lambda - (i_0 + \dots + i_n)\alpha $
for all
![]() $(i_0, \dots , i_n) \in \mathcal {I}$
, then we can choose
$(i_0, \dots , i_n) \in \mathcal {I}$
, then we can choose
![]() $\varphi $
to also be weight and hence in
$\varphi $
to also be weight and hence in
![]() $G_{\alpha } M$
.
$G_{\alpha } M$
.
Proof We construct elements
![]() $m_{i_0, \dots , i_n}$
for
$m_{i_0, \dots , i_n}$
for
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1} \backslash \mathcal {I}$
inductively such that the
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1} \backslash \mathcal {I}$
inductively such that the
![]() $m_{i_0, \dots , i_n}$
satisfy conditions (i) and (ii) above for any
$m_{i_0, \dots , i_n}$
satisfy conditions (i) and (ii) above for any
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
. Then observe that (i) and (ii) ensure that setting
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
. Then observe that (i) and (ii) ensure that setting
![]() $\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = m_{i_0, \dots , i_n}$
defines a
$\varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = m_{i_0, \dots , i_n}$
defines a
![]() $U(\mathfrak {a})$
-homomorphism
$U(\mathfrak {a})$
-homomorphism
![]() $\varphi : A \rightarrow \phi _{\alpha }^{-1}(M)$
, since it is enough to check that
$\varphi : A \rightarrow \phi _{\alpha }^{-1}(M)$
, since it is enough to check that
![]() $m_{i_0, \dots , i_k - 1, \dots i_n} = f_{\alpha , k} \cdot _{\alpha ^{-1}} \varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = f_{\alpha , k} \cdot _{\alpha ^{-1}} m_{i_0, \dots , i_n} = e_{\alpha , k} \cdot m_{i_0, \dots , i_n}$
for any
$m_{i_0, \dots , i_k - 1, \dots i_n} = f_{\alpha , k} \cdot _{\alpha ^{-1}} \varphi (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = f_{\alpha , k} \cdot _{\alpha ^{-1}} m_{i_0, \dots , i_n} = e_{\alpha , k} \cdot m_{i_0, \dots , i_n}$
for any
![]() $0 \leq k \leq n$
and
$0 \leq k \leq n$
and
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
.
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
.
To construct such
![]() $m_{i_0, \dots , i_n}$
, let
$m_{i_0, \dots , i_n}$
, let
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1} \backslash \mathcal {I}$
be such that
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1} \backslash \mathcal {I}$
be such that
![]() $i_0 + \dots + i_n$
is minimal among elements of
$i_0 + \dots + i_n$
is minimal among elements of
![]() $\mathbb {Z}^{n+1} \backslash \mathcal {I}$
. Then, in particular,
$\mathbb {Z}^{n+1} \backslash \mathcal {I}$
. Then, in particular,
![]() $(i_0, \dots , i_k - 1, \dots , i_n) \in \mathcal {I}$
for each
$(i_0, \dots , i_k - 1, \dots , i_n) \in \mathcal {I}$
for each
![]() $0 \leq k \leq n$
. Let
$0 \leq k \leq n$
. Let
![]() $(\mathfrak {sl}_2)_n$
be the truncated current algebra on the copy of
$(\mathfrak {sl}_2)_n$
be the truncated current algebra on the copy of
![]() $\mathfrak {sl}_2$
spanned by
$\mathfrak {sl}_2$
spanned by
![]() $e_{\alpha }, h_{\alpha }, f_{\alpha }$
, and let N be the
$e_{\alpha }, h_{\alpha }, f_{\alpha }$
, and let N be the
![]() $(\mathfrak {sl}_2)_n$
-module generated by
$(\mathfrak {sl}_2)_n$
-module generated by
![]() $\{m_{i_0, \dots , i_k - 1, \dots , i_n}: 0 \leq k \leq n\}$
, so
$\{m_{i_0, \dots , i_k - 1, \dots , i_n}: 0 \leq k \leq n\}$
, so
![]() $N \in \mathcal {O}^{(\mu )}((\mathfrak {sl}_2)_n)$
. Here, we make a slight abuse of notation, identifying
$N \in \mathcal {O}^{(\mu )}((\mathfrak {sl}_2)_n)$
. Here, we make a slight abuse of notation, identifying
![]() $\mu $
with the restriction to
$\mu $
with the restriction to
![]() $\mathfrak {h}_n \cap (\mathfrak {sl}_2)_n$
. Then we use the following claim to construct
$\mathfrak {h}_n \cap (\mathfrak {sl}_2)_n$
. Then we use the following claim to construct
![]() $m_{i_0, \dots , i_n} \in N \subseteq M$
such that
$m_{i_0, \dots , i_n} \in N \subseteq M$
such that
![]() $e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots , i_n}$
.
$e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots , i_n}$
.
Claim (*) Consider the maps
given by
![]() $\theta _1(x) = (e_{\alpha , 0} \cdot x, \dots , e_{\alpha , n} \cdot x)$
and
$\theta _1(x) = (e_{\alpha , 0} \cdot x, \dots , e_{\alpha , n} \cdot x)$
and
![]() $\theta _2(y_0, \dots , y_n) = (e_{\alpha , k} \cdot y_l - e_{\alpha , l} \cdot y_k)_{0 \leq k < l \leq n}$
. Then
$\theta _2(y_0, \dots , y_n) = (e_{\alpha , k} \cdot y_l - e_{\alpha , l} \cdot y_k)_{0 \leq k < l \leq n}$
. Then
![]() $\ker (\theta _2) = \operatorname {im}(\theta _1)$
. Furthermore, if
$\ker (\theta _2) = \operatorname {im}(\theta _1)$
. Furthermore, if
![]() $(y_0, \dots , y_n) \in \ker (\theta _2)$
and
$(y_0, \dots , y_n) \in \ker (\theta _2)$
and
![]() $y_k \in N \cap M^\lambda $
for all
$y_k \in N \cap M^\lambda $
for all
![]() $0 \leq k \leq n$
, then there exists
$0 \leq k \leq n$
, then there exists
![]() $x \in M^{\lambda - \alpha }$
such that
$x \in M^{\lambda - \alpha }$
such that
![]() $\theta _1(x) = (y_0, \dots , y_n)$
.
$\theta _1(x) = (y_0, \dots , y_n)$
.
We now prove the claim, which will take several steps.
First, observe that
![]() $\theta _2 \circ \theta _1 = 0$
, so certainly
$\theta _2 \circ \theta _1 = 0$
, so certainly
![]() $\ker (\theta _2) \supseteq \operatorname {im}(\theta _1)$
. Hence, we only need to show that
$\ker (\theta _2) \supseteq \operatorname {im}(\theta _1)$
. Hence, we only need to show that
![]() $\operatorname {im}(\theta _1) \supseteq \ker (\theta _2)$
. Throughout the proof of the claim, we write
$\operatorname {im}(\theta _1) \supseteq \ker (\theta _2)$
. Throughout the proof of the claim, we write
![]() $e_k$
for
$e_k$
for
![]() $e_{\alpha , k}$
.
$e_{\alpha , k}$
.
We first deal with the case where
![]() $n = 1$
and
$n = 1$
and
![]() $N = M_{\gamma }$
is a Verma module. In this case, we consider the restriction of these maps to certain weight spaces in the following way (for any
$N = M_{\gamma }$
is a Verma module. In this case, we consider the restriction of these maps to certain weight spaces in the following way (for any
![]() $\lambda \in \mathfrak {h}^{*}$
):
$\lambda \in \mathfrak {h}^{*}$
):
Now, either
![]() $\dim (N^{\lambda + \alpha }) = 0$
, in which case
$\dim (N^{\lambda + \alpha }) = 0$
, in which case
![]() $\operatorname {im}(\theta _1) = \ker (\theta _2)$
automatically, or the dimensions of these weight spaces satisfy
$\operatorname {im}(\theta _1) = \ker (\theta _2)$
automatically, or the dimensions of these weight spaces satisfy
![]() $\dim (N^\lambda ) = n + 1$
,
$\dim (N^\lambda ) = n + 1$
,
![]() $\dim (N^{\lambda + \alpha }) = n$
, and
$\dim (N^{\lambda + \alpha }) = n$
, and
![]() $\dim (N^{\lambda + 2\alpha }) = n - 1$
. Hence, by considering dimensions and the fact that
$\dim (N^{\lambda + 2\alpha }) = n - 1$
. Hence, by considering dimensions and the fact that
![]() $\ker (\theta _2) \supseteq \operatorname {im}(\theta _1)$
, it is enough to show that
$\ker (\theta _2) \supseteq \operatorname {im}(\theta _1)$
, it is enough to show that
![]() $\theta _1$
is injective and
$\theta _1$
is injective and
![]() $\theta _2$
is surjective. We can compute that
$\theta _2$
is surjective. We can compute that
![]() $e_1$
acts on the basis vectors
$e_1$
acts on the basis vectors
![]() $f_1^i f_0^j \otimes 1$
by
$f_1^i f_0^j \otimes 1$
by
so by considering
![]() $\theta _2(x, 0)$
, we see
$\theta _2(x, 0)$
, we see
![]() $\theta _2$
is surjective using (5.12) and an inductive argument. We also see that
$\theta _2$
is surjective using (5.12) and an inductive argument. We also see that
![]() $e_1 \cdot v = 0$
if and only if
$e_1 \cdot v = 0$
if and only if
![]() $v = f_1^i \otimes 1$
. Since
$v = f_1^i \otimes 1$
. Since
![]() $\mu \neq 0$
, we can show that
$\mu \neq 0$
, we can show that
![]() $e_0 \cdot f_1^i \otimes 1 \neq 0$
, so
$e_0 \cdot f_1^i \otimes 1 \neq 0$
, so
![]() $\theta _1$
is injective as required.
$\theta _1$
is injective as required.
We now deal with the case where
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $N = M_{\lambda }$
is a Verma in the
$N = M_{\lambda }$
is a Verma in the
![]() $\mu $
-Jordan block, so
$\mu $
-Jordan block, so
![]() $\lambda |_{\ge 1} = \mu $
. We use the following facts, which can be verified by computing the action of
$\lambda |_{\ge 1} = \mu $
. We use the following facts, which can be verified by computing the action of
![]() $e_n$
on the basis elements
$e_n$
on the basis elements
![]() $f_0^{i_0} \dots f_n^{i_n} \otimes 1$
of
$f_0^{i_0} \dots f_n^{i_n} \otimes 1$
of
![]() $M_{\lambda }$
and recalling that
$M_{\lambda }$
and recalling that
![]() $\mu (h_{\alpha }) \neq 0$
:
$\mu (h_{\alpha }) \neq 0$
:
-
(a)
 $e_n \cdot N = N$
, which uses an inductive argument with (5.12).
$e_n \cdot N = N$
, which uses an inductive argument with (5.12). -
(b)
 $e_n \cdot m = 0$
if and only if
$e_n \cdot m = 0$
if and only if
 $m \in \operatorname {span}\{f_1^{i_1} \dots f_n^{i_n} \otimes 1: i_1, \dots , i_n \geq 0\}$
. The latter is isomorphic as a
$m \in \operatorname {span}\{f_1^{i_1} \dots f_n^{i_n} \otimes 1: i_1, \dots , i_n \geq 0\}$
. The latter is isomorphic as a
 $U(\langle e_0, \dots , e_{n-1} \rangle )$
-module to the Verma module
$U(\langle e_0, \dots , e_{n-1} \rangle )$
-module to the Verma module
 $M_{\gamma }$
over
$M_{\gamma }$
over
 $\operatorname {span}\{ e_{\alpha , i}, h_{\alpha ,i}, f_{\alpha ,i} \mid i=0,...,n-1\} \cong ((\mathfrak {sl}_{2})_{\alpha })_{n-1}$
where
$\operatorname {span}\{ e_{\alpha , i}, h_{\alpha ,i}, f_{\alpha ,i} \mid i=0,...,n-1\} \cong ((\mathfrak {sl}_{2})_{\alpha })_{n-1}$
where
 $\gamma (h_{\alpha , i}) := \mu (h_{\alpha , i+1})$
.
$\gamma (h_{\alpha , i}) := \mu (h_{\alpha , i+1})$
. -
(c) Applying (b) repeatedly, we see that for any
 $k \geq 1$
, we have that
$k \geq 1$
, we have that
 $e_l \cdot m = 0$
for all
$e_l \cdot m = 0$
for all
 $k \leq l \leq n$
if and only if
$k \leq l \leq n$
if and only if
 $m \in \operatorname {span}\{f_{n-k+1}^{i_{n-k+1}} \dots f_n^{i_n} \otimes 1: i_{n-k+1}, \dots , i_n \geq 0\}$
.
$m \in \operatorname {span}\{f_{n-k+1}^{i_{n-k+1}} \dots f_n^{i_n} \otimes 1: i_{n-k+1}, \dots , i_n \geq 0\}$
.
To ease notation slightly, we will write
![]() $\mathfrak {a}_{(i)} = \langle e_0,...,e_i\rangle $
, and write
$\mathfrak {a}_{(i)} = \langle e_0,...,e_i\rangle $
, and write
![]() $(\mathfrak {sl}_2)_{(i)}$
for the Lie algebra
$(\mathfrak {sl}_2)_{(i)}$
for the Lie algebra
![]() $((\mathfrak {sl}_2)_{\alpha })_i$
and
$((\mathfrak {sl}_2)_{\alpha })_i$
and
![]() $\gamma _{(i)}$
for the character of
$\gamma _{(i)}$
for the character of
![]() $\operatorname {span}\{h_{\alpha , 0},..., h_{\alpha ,i}\}$
given by
$\operatorname {span}\{h_{\alpha , 0},..., h_{\alpha ,i}\}$
given by
![]() $\gamma _{(i)}(h_{\alpha ,j}) := \mu (h_{\alpha , n-i})$
.
$\gamma _{(i)}(h_{\alpha ,j}) := \mu (h_{\alpha , n-i})$
.
Now, let
![]() $(y_0, \dots , y_n) \in \ker (\theta _2)$
, i.e.,
$(y_0, \dots , y_n) \in \ker (\theta _2)$
, i.e.,
![]() $e_k \cdot y_l - e_l \cdot y_k = 0$
for all
$e_k \cdot y_l - e_l \cdot y_k = 0$
for all
![]() $0 \leq k, l \leq n$
. By fact (a), there certainly exists an
$0 \leq k, l \leq n$
. By fact (a), there certainly exists an
![]() $x_n$
such that
$x_n$
such that
![]() $e_n \cdot x_n = y_n$
. We then inductively construct
$e_n \cdot x_n = y_n$
. We then inductively construct
![]() $x_k$
for
$x_k$
for
![]() $2 \leq k \leq n$
such that
$2 \leq k \leq n$
such that
![]() $e_l \cdot x_k = y_l$
for all
$e_l \cdot x_k = y_l$
for all
![]() $k \leq l \leq n$
. Note that the cases
$k \leq l \leq n$
. Note that the cases
![]() $k = 0, 1$
will be dealt with by an additional argument immediately afterward, and we will then obtain
$k = 0, 1$
will be dealt with by an additional argument immediately afterward, and we will then obtain
![]() $x_0,...,x_n$
such that
$x_0,...,x_n$
such that
![]() $\theta (x_0,...,x_n) = (y_0,...,y_n)$
.
$\theta (x_0,...,x_n) = (y_0,...,y_n)$
.
Suppose we have constructed
![]() $x_{k+1}$
such that
$x_{k+1}$
such that
![]() $e_l \cdot x_{k+1} = y_l$
for all
$e_l \cdot x_{k+1} = y_l$
for all
![]() $k+1 \leq l \leq n$
. For any
$k+1 \leq l \leq n$
. For any
![]() $k+1 \leq l \leq n$
, consider
$k+1 \leq l \leq n$
, consider
![]() $e_l \cdot (e_k \cdot x_{k+1} - y_k) = e_k \cdot (e_l \cdot x_{k+1}) - e_l \cdot y_k = e_k \cdot y_l - e_l \cdot y_k = 0$
. Hence, by fact (c), we have
$e_l \cdot (e_k \cdot x_{k+1} - y_k) = e_k \cdot (e_l \cdot x_{k+1}) - e_l \cdot y_k = e_k \cdot y_l - e_l \cdot y_k = 0$
. Hence, by fact (c), we have
![]() $e_k \cdot x_{k+1} - y_k \in \operatorname {span}\{f_{n-k}^{i_{n-k}} \dots f_n^{i_n} \otimes 1: i_{n-k}, \dots , i_n \geq 0\}$
. But as a
$e_k \cdot x_{k+1} - y_k \in \operatorname {span}\{f_{n-k}^{i_{n-k}} \dots f_n^{i_n} \otimes 1: i_{n-k}, \dots , i_n \geq 0\}$
. But as a
![]() $U(\mathfrak {a}_{(k)})$
-module, this is isomorphic to
$U(\mathfrak {a}_{(k)})$
-module, this is isomorphic to
![]() $M_{\gamma _{(k)}}$
, so by fact (a), there exists
$M_{\gamma _{(k)}}$
, so by fact (a), there exists
![]() $x_k^{\prime } \in \operatorname {span}\{f_{n-k}^{i_{n-k}} \dots f_n^{i_n} \otimes 1: i_{n-k}, \dots , i_n \geq 0\}$
such that
$x_k^{\prime } \in \operatorname {span}\{f_{n-k}^{i_{n-k}} \dots f_n^{i_n} \otimes 1: i_{n-k}, \dots , i_n \geq 0\}$
such that
![]() $e_k \cdot x_k^{\prime } = e_k \cdot x_{k+1} - y_k$
, and by fact (c)
$e_k \cdot x_k^{\prime } = e_k \cdot x_{k+1} - y_k$
, and by fact (c)
![]() $e_l \cdot x_k^{\prime } = 0$
for all
$e_l \cdot x_k^{\prime } = 0$
for all
![]() $k+1 \leq l \leq n$
. Setting
$k+1 \leq l \leq n$
. Setting
![]() $x_k = x_{k+1} - x_k^{\prime }$
, we see that
$x_k = x_{k+1} - x_k^{\prime }$
, we see that
![]() $e_k \cdot x_k = e_k \cdot x_{k+1} - e_k \cdot x_k^{\prime } = e_k \cdot x_{k+1} - (e_k \cdot x_{k+1} - y_k) = y_k$
, and for
$e_k \cdot x_k = e_k \cdot x_{k+1} - e_k \cdot x_k^{\prime } = e_k \cdot x_{k+1} - (e_k \cdot x_{k+1} - y_k) = y_k$
, and for
![]() $k+1 \leq l \leq n$
, we have
$k+1 \leq l \leq n$
, we have
![]() $e_l \cdot x_k = e_l \cdot x_{k+1} - e_l \cdot x_k^{\prime } = y_l - 0$
. Hence, we have constructed
$e_l \cdot x_k = e_l \cdot x_{k+1} - e_l \cdot x_k^{\prime } = y_l - 0$
. Hence, we have constructed
![]() $x_k$
with the desired properties.
$x_k$
with the desired properties.
Now, consider
![]() $y_1^{\prime } = e_1 \cdot x_2 - y_1$
and
$y_1^{\prime } = e_1 \cdot x_2 - y_1$
and
![]() $y_0^{\prime } = e_0 \cdot x_2 - y_0$
. For
$y_0^{\prime } = e_0 \cdot x_2 - y_0$
. For
![]() $2 \leq l \leq n$
, we have
$2 \leq l \leq n$
, we have
![]() $e_l \cdot y_1^{\prime } = e_l \cdot (e_1 \cdot x_2 - y_1) = e_1 \cdot y_1 - e_l \cdot y_1 = 0$
, and similarly
$e_l \cdot y_1^{\prime } = e_l \cdot (e_1 \cdot x_2 - y_1) = e_1 \cdot y_1 - e_l \cdot y_1 = 0$
, and similarly
![]() $e_l \cdot y_0^{\prime } = 0$
, so
$e_l \cdot y_0^{\prime } = 0$
, so
![]() $y_0^{\prime }, y_1^{\prime } \in \operatorname {span}\{f_{n-1}^{i_{n-1}} f_n^{i_n} \otimes 1: i_{n-1}, i_n \geq 0\}$
, which is isomorphic to
$y_0^{\prime }, y_1^{\prime } \in \operatorname {span}\{f_{n-1}^{i_{n-1}} f_n^{i_n} \otimes 1: i_{n-1}, i_n \geq 0\}$
, which is isomorphic to
![]() $M_{\gamma _{(1)}}$
(Verma module over
$M_{\gamma _{(1)}}$
(Verma module over
![]() $((\mathfrak {sl}_2)_{(1)}$
) as a
$((\mathfrak {sl}_2)_{(1)}$
) as a
![]() $U(\langle e_0, e_1 \rangle )$
-module. In addition, since
$U(\langle e_0, e_1 \rangle )$
-module. In addition, since
![]() $(y_0,...,y_n) \in \ker \theta $
, we have
$(y_0,...,y_n) \in \ker \theta $
, we have
![]() $e_0 \cdot y_1^{\prime } - e_1 \cdot y_0^{\prime } = 0$
, so we can apply the case where N is a Verma module and
$e_0 \cdot y_1^{\prime } - e_1 \cdot y_0^{\prime } = 0$
, so we can apply the case where N is a Verma module and
![]() $n=1$
, proved earlier, to find
$n=1$
, proved earlier, to find
![]() $x'$
such that
$x'$
such that
![]() $e_0 \cdot x' = y_0^{\prime }$
,
$e_0 \cdot x' = y_0^{\prime }$
,
![]() $e_1 \cdot x' = y_1^{\prime }$
, and
$e_1 \cdot x' = y_1^{\prime }$
, and
![]() $e_l \cdot x' = 0$
for
$e_l \cdot x' = 0$
for
![]() $2 \leq l \leq n$
. Then setting
$2 \leq l \leq n$
. Then setting
![]() $x = x_2 - x'$
, we have that
$x = x_2 - x'$
, we have that
![]() $\theta _1(x) = (y_0, \dots , y_n)$
.
$\theta _1(x) = (y_0, \dots , y_n)$
.
If N is not a Verma module, let
![]() $0 = N_0 \subseteq N_1 \subseteq \dots \subseteq N_{k-1} \subseteq N_k = N$
be a filtration of N such that each quotient is a highest weight module. Since
$0 = N_0 \subseteq N_1 \subseteq \dots \subseteq N_{k-1} \subseteq N_k = N$
be a filtration of N such that each quotient is a highest weight module. Since
![]() $\mu (h_{\alpha }) \neq 0$
, all these highest weight modules must in fact be Verma modules by [Reference WilsonWi11, Theorem 7.1]. Then, given
$\mu (h_{\alpha }) \neq 0$
, all these highest weight modules must in fact be Verma modules by [Reference WilsonWi11, Theorem 7.1]. Then, given
![]() $(y_0, \dots , y_n) \in \ker (\theta _2)$
, in the quotient
$(y_0, \dots , y_n) \in \ker (\theta _2)$
, in the quotient
![]() $N/N_{k-1}$
, we have that there exists
$N/N_{k-1}$
, we have that there exists
![]() $x \in N$
such that
$x \in N$
such that
![]() $e_l \cdot x + N_{k-1} {\kern-1pt}={\kern-1pt} y_l + N_{k-1}$
for all
$e_l \cdot x + N_{k-1} {\kern-1pt}={\kern-1pt} y_l + N_{k-1}$
for all
![]() $0 {\kern-1pt}\leq{\kern-1pt} l {\kern-1pt}\leq{\kern-1pt} n$
. Hence,
$0 {\kern-1pt}\leq{\kern-1pt} l {\kern-1pt}\leq{\kern-1pt} n$
. Hence,
![]() $e_l \cdot x - y_l {\kern-1pt}\in{\kern-1pt} N_{k-1}$
for all
$e_l \cdot x - y_l {\kern-1pt}\in{\kern-1pt} N_{k-1}$
for all
![]() $0 \leq l \leq n$
. But
$0 \leq l \leq n$
. But
![]() $e_{l'} \cdot (e_l \cdot x - y_l) = e_l \cdot (e_{l'} \cdot x - y_{l'})$
for all
$e_{l'} \cdot (e_l \cdot x - y_l) = e_l \cdot (e_{l'} \cdot x - y_{l'})$
for all
![]() $0 \leq l, l', \leq n$
, so by induction on k, there exists
$0 \leq l, l', \leq n$
, so by induction on k, there exists
![]() $x' \in N_{k-1}$
such that
$x' \in N_{k-1}$
such that
![]() $e_l \cdot x' = e_l \cdot x - y_l$
for all
$e_l \cdot x' = e_l \cdot x - y_l$
for all
![]() $0 \leq l \leq n$
. Note that in this final argument, we have used the fact that
$0 \leq l \leq n$
. Note that in this final argument, we have used the fact that
![]() $y_l^{\prime } := e_l \cdot x - y_l$
gives a collection of elements lying in the kernel of
$y_l^{\prime } := e_l \cdot x - y_l$
gives a collection of elements lying in the kernel of
![]() $\theta $
, which allows us to apply the inductive hypothesis. Hence,
$\theta $
, which allows us to apply the inductive hypothesis. Hence,
![]() $e_l \cdot (x-x') = y_l$
for all
$e_l \cdot (x-x') = y_l$
for all
![]() $0 \leq l \leq n$
, so
$0 \leq l \leq n$
, so
![]() $\operatorname {im}(\theta _1) \supseteq \ker (\theta _2)$
as required.
$\operatorname {im}(\theta _1) \supseteq \ker (\theta _2)$
as required.
Finally, if
![]() $y_0, \dots , y_n \in M^\lambda \cap N$
, then given
$y_0, \dots , y_n \in M^\lambda \cap N$
, then given
![]() $x \in N \subseteq M$
such that
$x \in N \subseteq M$
such that
![]() $\theta _1(x) = (y_0, \dots , y_n)$
, by considering weight spaces, we may replace x with its component
$\theta _1(x) = (y_0, \dots , y_n)$
, by considering weight spaces, we may replace x with its component
![]() $x^{\lambda - \alpha }$
in the
$x^{\lambda - \alpha }$
in the
![]() $\lambda - \alpha $
weight space and
$\lambda - \alpha $
weight space and
![]() $\theta _1(x) = \theta _1(x^{\lambda - \alpha })$
, proving the final part of Claim
$\theta _1(x) = \theta _1(x^{\lambda - \alpha })$
, proving the final part of Claim
![]() $(\ast )$
.
$(\ast )$
.
Since
![]() $e_{\alpha , k} \cdot m_{i_0, \dots , i_l -1, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots , i_l - 1, \dots i_n} = e_{\alpha , l} \cdot m_{i_0, \dots , i_k - 1, \dots i_n}$
for all
$e_{\alpha , k} \cdot m_{i_0, \dots , i_l -1, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots , i_l - 1, \dots i_n} = e_{\alpha , l} \cdot m_{i_0, \dots , i_k - 1, \dots i_n}$
for all
![]() $0 \leq k < l \leq n$
, this claim then allows us to pick
$0 \leq k < l \leq n$
, this claim then allows us to pick
![]() $m_{i_0, \dots , i_n}$
such that
$m_{i_0, \dots , i_n}$
such that
![]() $e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots i_n}$
for all
$e_{\alpha , k} \cdot m_{i_0, \dots , i_n} = m_{i_0, \dots , i_k - 1, \dots i_n}$
for all
![]() $0 \leq k \leq n$
, and if
$0 \leq k \leq n$
, and if
![]() $m_{i_0, \dots , i_k-1, \dots , i_n}$
has weight
$m_{i_0, \dots , i_k-1, \dots , i_n}$
has weight
![]() $\lambda $
for all
$\lambda $
for all
![]() $0 \leq k \leq n$
, then we can choose
$0 \leq k \leq n$
, then we can choose
![]() $m_{i_0, \dots , i_n}$
to have weight
$m_{i_0, \dots , i_n}$
to have weight
![]() $\lambda - \alpha $
. Hence, applying this inductively, we can construct for all
$\lambda - \alpha $
. Hence, applying this inductively, we can construct for all
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
elements
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
elements
![]() $m_{i_0, \dots , i_n} \in M$
satisfying conditions (i) and (ii).
$m_{i_0, \dots , i_n} \in M$
satisfying conditions (i) and (ii).
Suppose there exists
![]() $\lambda \in \mathfrak {h}^{*}$
such that
$\lambda \in \mathfrak {h}^{*}$
such that
![]() $\operatorname {wt}(m_{i_0, \dots , i_n}) = \lambda - (i_0 + \dots + i_n)\alpha $
for all
$\operatorname {wt}(m_{i_0, \dots , i_n}) = \lambda - (i_0 + \dots + i_n)\alpha $
for all
![]() $(i_0, \dots , i_n) \in \mathcal {I}$
. Then, by construction,
$(i_0, \dots , i_n) \in \mathcal {I}$
. Then, by construction,
![]() $m_{i_0, \dots , i_n}$
is weight for all
$m_{i_0, \dots , i_n}$
is weight for all
![]() $(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
, so by Corollary 5.7, the homomorphism we have constructed is a weight vector.
$(i_0, \dots , i_n) \in \mathbb {Z}^{n+1}$
, so by Corollary 5.7, the homomorphism we have constructed is a weight vector.
We are now ready to establish one of the main ingredients toward the proof of Theorem 5.9.
Lemma 5.16 For any
![]() $N {\kern-1pt}\in{\kern-1pt} \mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n)$
, the map
$N {\kern-1pt}\in{\kern-1pt} \mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n)$
, the map
![]() $\epsilon _N {\kern-1pt}:{\kern-1pt} T_{\alpha } G_{\alpha } N \rightarrow N$
given by
$\epsilon _N {\kern-1pt}:{\kern-1pt} T_{\alpha } G_{\alpha } N \rightarrow N$
given by
![]() $\epsilon _N(s \otimes g) = g(s)$
is an isomorphism.
$\epsilon _N(s \otimes g) = g(s)$
is an isomorphism.
Proof First, we show
![]() $\epsilon _N$
is a homomorphism. Let
$\epsilon _N$
is a homomorphism. Let
![]() $u \in U$
, let
$u \in U$
, let
![]() $s \in S_{\alpha }$
, and let
$s \in S_{\alpha }$
, and let
![]() $g \in G_{\alpha } N$
. Then
$g \in G_{\alpha } N$
. Then
 $$\begin{align*}u \cdot \epsilon_N(s \otimes g) &= u \cdot g(s) = \phi_{\alpha}^{-1} \phi_{\alpha} (u) \cdot g(s) = g(\phi_{\alpha}(u) \cdot s) = \epsilon_N((\phi_{\alpha}(u) \cdot s) \otimes g)\\ &= \epsilon_N(u \cdot (s \otimes g)),\end{align*}$$
$$\begin{align*}u \cdot \epsilon_N(s \otimes g) &= u \cdot g(s) = \phi_{\alpha}^{-1} \phi_{\alpha} (u) \cdot g(s) = g(\phi_{\alpha}(u) \cdot s) = \epsilon_N((\phi_{\alpha}(u) \cdot s) \otimes g)\\ &= \epsilon_N(u \cdot (s \otimes g)),\end{align*}$$
so
![]() $\epsilon _N$
is certainly a U-homomorphism.
$\epsilon _N$
is certainly a U-homomorphism.
Now, let
![]() $m \in N$
be a weight vector, and choose
$m \in N$
be a weight vector, and choose
![]() $a_0, \dots , a_n$
such that
$a_0, \dots , a_n$
such that
![]() $e_{\alpha , k}^{a_k} \cdot m = 0$
for each k. Let
$e_{\alpha , k}^{a_k} \cdot m = 0$
for each k. Let
 $$ \begin{align*} \mathcal{I} &= \{(i_0, \dots, i_n) : i_k \leq 0 \mbox{ for some } k \mbox{ or } i_k \leq a_k \mbox{ for all } k\} \subseteq \mathbb{Z}^{n+1}\\ m_{i_0, \dots, i_n} &= e_{\alpha, 0}^{a_0 - i_0} \dots e_{\alpha, n}^{a_n - i_n} \cdot m \mbox{ if } i_k \leq a_k \mbox{ for all } k\\ m_{i_0, \dots, i_n} &= 0 \mbox{ otherwise.} \end{align*} $$
$$ \begin{align*} \mathcal{I} &= \{(i_0, \dots, i_n) : i_k \leq 0 \mbox{ for some } k \mbox{ or } i_k \leq a_k \mbox{ for all } k\} \subseteq \mathbb{Z}^{n+1}\\ m_{i_0, \dots, i_n} &= e_{\alpha, 0}^{a_0 - i_0} \dots e_{\alpha, n}^{a_n - i_n} \cdot m \mbox{ if } i_k \leq a_k \mbox{ for all } k\\ m_{i_0, \dots, i_n} &= 0 \mbox{ otherwise.} \end{align*} $$
Then we can use Lemma 5.15 to construct
![]() $\varphi \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, which is a weight vector and therefore in
$\varphi \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, which is a weight vector and therefore in
![]() $G_{\alpha } N$
such that
$G_{\alpha } N$
such that
![]() $\varphi (f_{\alpha , 0}^{-a_0} \dots f_{\alpha , n}^{-a_n}) = m$
. Hence,
$\varphi (f_{\alpha , 0}^{-a_0} \dots f_{\alpha , n}^{-a_n}) = m$
. Hence,
![]() $\epsilon _N(f_{\alpha , 0}^{-a_0} \dots f_{\alpha , n}^{-a_n} \otimes \varphi ) = m$
, so
$\epsilon _N(f_{\alpha , 0}^{-a_0} \dots f_{\alpha , n}^{-a_n} \otimes \varphi ) = m$
, so
![]() $\epsilon _N$
is surjective.
$\epsilon _N$
is surjective.
We now show
![]() $\epsilon _N$
is injective. By Lemma 5.12, any element of
$\epsilon _N$
is injective. By Lemma 5.12, any element of
![]() $T_{\alpha } G_{\alpha } N$
may be written as
$T_{\alpha } G_{\alpha } N$
may be written as
![]() $f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g$
for some
$f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g$
for some
![]() $g \in G_{\alpha } N$
. Suppose
$g \in G_{\alpha } N$
. Suppose
![]() $\epsilon _N(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g) = g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = 0$
. We may assume g is weight (i.e., an
$\epsilon _N(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g) = g(f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = 0$
. We may assume g is weight (i.e., an
![]() $\mathfrak {h}$
-eigenvector). If not, we may write g as a sum of
$\mathfrak {h}$
-eigenvector). If not, we may write g as a sum of
![]() $g_\lambda \in (G_{\alpha } N)^\lambda $
, which, by considering weight spaces, must all satisfy
$g_\lambda \in (G_{\alpha } N)^\lambda $
, which, by considering weight spaces, must all satisfy
![]() $g_\lambda (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = 0$
, and then apply the following argument to each
$g_\lambda (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) = 0$
, and then apply the following argument to each
![]() $g_\lambda $
.
$g_\lambda $
.
Observe that
Now, choose
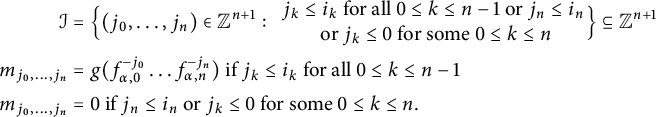 $$ \begin{align*} \mathcal{I} &= \Big\{(j_0, \dots, j_n) \in \mathbb{Z}^{n+1} : \begin{array}{c} j_k \leq i_k \mbox{ for all } 0 \leq k \leq n-1 \mbox{ or } j_n \leq i_n \\ \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n\end{array} \!\!\!\Big\} \subseteq \mathbb{Z}^{n+1} \\ m_{j_0, \dots, j_n} &= g(f_{\alpha, 0}^{-j_0} \dots f_{\alpha, n}^{-j_n}) \mbox{ if } j_k \leq i_k \mbox{ for all } 0 \leq k \leq n-1\\ m_{j_0, \dots, j_n} &= 0 \mbox{ if } j_n \leq i_n \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n. \end{align*} $$
$$ \begin{align*} \mathcal{I} &= \Big\{(j_0, \dots, j_n) \in \mathbb{Z}^{n+1} : \begin{array}{c} j_k \leq i_k \mbox{ for all } 0 \leq k \leq n-1 \mbox{ or } j_n \leq i_n \\ \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n\end{array} \!\!\!\Big\} \subseteq \mathbb{Z}^{n+1} \\ m_{j_0, \dots, j_n} &= g(f_{\alpha, 0}^{-j_0} \dots f_{\alpha, n}^{-j_n}) \mbox{ if } j_k \leq i_k \mbox{ for all } 0 \leq k \leq n-1\\ m_{j_0, \dots, j_n} &= 0 \mbox{ if } j_n \leq i_n \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n. \end{align*} $$
Then, applying Lemma 5.15 to this, we construct
![]() $g_n \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, which is a weight vector (and hence in
$g_n \in \operatorname {Hom}_U(S_{\alpha }, \phi _{\alpha }^{-1}(M))$
, which is a weight vector (and hence in
![]() $G_{\alpha } N$
) such that:
$G_{\alpha } N$
) such that:
-
(a)
 $g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
$g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
 $j_n \leq i_n$
,
$j_n \leq i_n$
, -
(b)
 $g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = g(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
if
$g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = g(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
if
 $j_k \leq i_k$
for all
$j_k \leq i_k$
for all
 $0 \leq k \leq n-1$
.
$0 \leq k \leq n-1$
.
Note that these two conditions are not mutually exclusive, but they are consistent by (5.13).
By (a), we can define
![]() $g_n^{\prime } \in G_{\alpha } N$
by setting
$g_n^{\prime } \in G_{\alpha } N$
by setting
![]() $g_n^{\prime }(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n-1}^{-j_{n-1}} f_{\alpha , n}^{-j_n+i_n}) = g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
and so
$g_n^{\prime }(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n-1}^{-j_{n-1}} f_{\alpha , n}^{-j_n+i_n}) = g_n(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
and so
![]() $g_n = f_{\alpha , n}^{i_n} \cdot g_n^{\prime }$
. By (b), we have
$g_n = f_{\alpha , n}^{i_n} \cdot g_n^{\prime }$
. By (b), we have
![]() $(g - g_n)(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if either some
$(g - g_n)(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if either some
![]() $j_k \leq 0$
or if
$j_k \leq 0$
or if
![]() $j_k \leq i_k$
for all
$j_k \leq i_k$
for all
![]() $0 \leq k \leq n-1$
.
$0 \leq k \leq n-1$
.
We now construct
![]() $g_s \in G_{\alpha } N$
inductively by setting
$g_s \in G_{\alpha } N$
inductively by setting
 $$ \begin{align*} \mathcal{I} &= \{(j_0, \dots, j_n) \in \mathbb{Z}^{n+1} : j_k \leq i_k \mbox{ for all } 0 \leq k \leq s-1 \mbox{ or } j_s \leq i_s \mbox{ or } j_k \leq 0\\ & \qquad\mbox{ for some } 0 \leq k \leq n\} \subseteq \mathbb{Z}^{n+1} \\ m_{j_0, \dots, j_n} &= (g - g_n - \dots - g_{s+1})(f_{\alpha, 0}^{-j_0} \dots f_{\alpha, n}^{-j_n}) \mbox{ if } j_k \leq i_k \mbox{ for all } 0 \leq k \leq s-1\\ m_{j_0, \dots, j_n} &= 0 \mbox{ if } j_s \leq i_s \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n. \end{align*} $$
$$ \begin{align*} \mathcal{I} &= \{(j_0, \dots, j_n) \in \mathbb{Z}^{n+1} : j_k \leq i_k \mbox{ for all } 0 \leq k \leq s-1 \mbox{ or } j_s \leq i_s \mbox{ or } j_k \leq 0\\ & \qquad\mbox{ for some } 0 \leq k \leq n\} \subseteq \mathbb{Z}^{n+1} \\ m_{j_0, \dots, j_n} &= (g - g_n - \dots - g_{s+1})(f_{\alpha, 0}^{-j_0} \dots f_{\alpha, n}^{-j_n}) \mbox{ if } j_k \leq i_k \mbox{ for all } 0 \leq k \leq s-1\\ m_{j_0, \dots, j_n} &= 0 \mbox{ if } j_s \leq i_s \mbox{ or } j_k \leq 0 \mbox{ for some } 0 \leq k \leq n. \end{align*} $$
The element
![]() $g - g_n - \dots - g_{s+1}$
satisfies a condition analogous to (5.13), which means that the definition of
$g - g_n - \dots - g_{s+1}$
satisfies a condition analogous to (5.13), which means that the definition of
![]() $m_{j_0,...,j_n}$
is consistent.
$m_{j_0,...,j_n}$
is consistent.
This
![]() $g_s$
satisfies:
$g_s$
satisfies:
-
(a)
 $g_s(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
$g_s(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
 $j_s \leq i_s$
,
$j_s \leq i_s$
, -
(b)
 $g_s(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = (g - g_n - \dots - g_{s+1})(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
if
$g_s(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = (g - g_n - \dots - g_{s+1})(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n})$
if
 $j_k \leq i_k$
for all
$j_k \leq i_k$
for all
 $0 \leq k \leq s-1$
.
$0 \leq k \leq s-1$
.
By (a), we can write this
![]() $g_s$
in the form
$g_s$
in the form
![]() $g_s = f_{\alpha , s}^{i_s} \cdot g_s^{\prime }$
for some
$g_s = f_{\alpha , s}^{i_s} \cdot g_s^{\prime }$
for some
![]() $g_s^{\prime } \in G_{\alpha } N$
. By (b), we have that
$g_s^{\prime } \in G_{\alpha } N$
. By (b), we have that
![]() $(g - g_n - \dots - g_s)(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
$(g - g_n - \dots - g_s)(f_{\alpha , 0}^{-j_0} \dots f_{\alpha , n}^{-j_n}) = 0$
if
![]() $j_k \leq i_k$
for all
$j_k \leq i_k$
for all
![]() $0 \leq k \leq s-1$
. Hence, we see that
$0 \leq k \leq s-1$
. Hence, we see that
![]() $g = f_{\alpha , 0}^{-i_0} \cdot g_0^{\prime } + \dots + f_{\alpha , n}^{-i_n} \cdot g_n^{\prime }$
for some
$g = f_{\alpha , 0}^{-i_0} \cdot g_0^{\prime } + \dots + f_{\alpha , n}^{-i_n} \cdot g_n^{\prime }$
for some
![]() $g_0^{\prime }, \dots , g_n^{\prime } \in G_{\alpha } N$
, so
$g_0^{\prime }, \dots , g_n^{\prime } \in G_{\alpha } N$
, so
![]() $f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g = \sum (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) \otimes f_{\alpha , k}^{i_k} g_k^{\prime } = 0$
. Hence,
$f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n} \otimes g = \sum (f_{\alpha , 0}^{-i_0} \dots f_{\alpha , n}^{-i_n}) \otimes f_{\alpha , k}^{i_k} g_k^{\prime } = 0$
. Hence,
![]() $\epsilon _N$
is injective.
$\epsilon _N$
is injective.
The proof of this next lemma is almost identical to [Reference ChaffeCh23, Lemma 5.8], and so we skip it for the sake of brevity.
Lemma 5.17
![]() $G_{\alpha }$
restricts to a functor
$G_{\alpha }$
restricts to a functor
![]() $\mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n) \rightarrow \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
.
$\mathcal {O}^{(s_{\alpha }(\mu ))}(\mathfrak {g}_n) \rightarrow \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
.
This next result can be checked by following the argument for [Reference ChaffeCh23, Lemma 5.8(e)] verbatim.
Lemma 5.18 The transformations
and
are natural.
Finally, Theorem 5.9 follows by combining Lemmas 5.10, 5.13, and 5.16–5.18.
6 Composition multiplicities
6.1 Definition of composition multiplicity
Let
![]() $M \in \mathcal {O}(\mathfrak {g}_n)$
. We define the character of M to be the function
$M \in \mathcal {O}(\mathfrak {g}_n)$
. We define the character of M to be the function
![]() $\operatorname {ch}(M): \mathfrak {h}^{*} \rightarrow \mathbb {Z}_{\geq 0}$
which sends
$\operatorname {ch}(M): \mathfrak {h}^{*} \rightarrow \mathbb {Z}_{\geq 0}$
which sends
![]() $\lambda $
to
$\lambda $
to
![]() $\operatorname {dim}(M^\lambda )$
, and the support of M, denoted
$\operatorname {dim}(M^\lambda )$
, and the support of M, denoted
![]() $\operatorname {supp}(M)$
, to be the set
$\operatorname {supp}(M)$
, to be the set
![]() $\operatorname {supp}(M) = \{\lambda \in \mathfrak {h}^{*} : M^\lambda \neq 0\}$
.
$\operatorname {supp}(M) = \{\lambda \in \mathfrak {h}^{*} : M^\lambda \neq 0\}$
.
We define the composition multiplicities
![]() $k_\lambda (M)$
of M for
$k_\lambda (M)$
of M for
![]() $\lambda \in \mathfrak {h}^{*}$
using the following result, whose statement and proof are very similar to [Reference ChaffeCh23, Lemma 6.1] or [Reference Mazorchuk and SöderbergMSo19, Proposition 8].
$\lambda \in \mathfrak {h}^{*}$
using the following result, whose statement and proof are very similar to [Reference ChaffeCh23, Lemma 6.1] or [Reference Mazorchuk and SöderbergMSo19, Proposition 8].
Lemma 6.1 Let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
. For any
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
. For any
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, there are unique
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
, there are unique
![]() $\{k_\lambda (M) \in \mathbb {Z}_{\geq 0} : \lambda \in \mathfrak {h}_n^{*}, \lambda _{\geq 1} = \mu \}$
, which we refer to as composition multiplicities, such that
$\{k_\lambda (M) \in \mathbb {Z}_{\geq 0} : \lambda \in \mathfrak {h}_n^{*}, \lambda _{\geq 1} = \mu \}$
, which we refer to as composition multiplicities, such that
We give another interpretation of these, which is closer to the notion of composition multiplicities in Artinian categories. The following result is a natural generalization of [Reference ChaffeCh23, Lemma 6.2].
Lemma 6.2 Let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
and
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
and
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
. Then there exist
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
. Then there exist
![]() $\mathcal {I} \subseteq (\mathbb {Z}_{\geq 0})^n$
and a descending filtration of M indexed by
$\mathcal {I} \subseteq (\mathbb {Z}_{\geq 0})^n$
and a descending filtration of M indexed by
![]() $\mathcal {I}$
with the lexicographic ordering such that:
$\mathcal {I}$
with the lexicographic ordering such that:
-
(a) If
 $(i_1, \dots , i_{k-1}, i_k, \dots , i_n) \in \mathcal {I}$
with
$(i_1, \dots , i_{k-1}, i_k, \dots , i_n) \in \mathcal {I}$
with
 $i_k> 0$
, then
$i_k> 0$
, then
 $(i_1, \dots , i_{k-1}, i_k-1, 0, \dots , 0) \in \mathcal {I}$
.
$(i_1, \dots , i_{k-1}, i_k-1, 0, \dots , 0) \in \mathcal {I}$
. -
(b) Each quotient
 $M_{(i_1, \dots , i_n-1)}/M_{(i_1, \dots , i_n)}$
is simple.
$M_{(i_1, \dots , i_n-1)}/M_{(i_1, \dots , i_n)}$
is simple. -
(c) The intersection of all the
 $M_{(i_1, \dots , i_n)}$
is 0.
$M_{(i_1, \dots , i_n)}$
is 0.
Furthermore, for any such filtration,
![]() $L_{\lambda }$
appears as a quotient
$L_{\lambda }$
appears as a quotient
![]() $M_{(i_1, \dots , i_n-1)}/M_{(i_1, \dots , i_n)}$
precisely
$M_{(i_1, \dots , i_n-1)}/M_{(i_1, \dots , i_n)}$
precisely
![]() $k_\lambda (M)$
times.
$k_\lambda (M)$
times.
Proof First, observe that by Theorems 4.1 and 5.9, we may reduce to the case
![]() $\mu (\mathfrak {h}_n^n) = 0$
.
$\mu (\mathfrak {h}_n^n) = 0$
.
Recall the notation
![]() $\mathfrak {g}_n^n = \mathfrak {g} \otimes t^n \subseteq \mathfrak {g}_n$
.
$\mathfrak {g}_n^n = \mathfrak {g} \otimes t^n \subseteq \mathfrak {g}_n$
.
First, suppose
![]() $n = 1$
. In this case, M has a filtration
$n = 1$
. In this case, M has a filtration
![]() $M \supseteq \mathfrak {g}_1^1 M \supseteq (\mathfrak {g}_1^1)^2 M \supseteq \cdots $
. Each quotient
$M \supseteq \mathfrak {g}_1^1 M \supseteq (\mathfrak {g}_1^1)^2 M \supseteq \cdots $
. Each quotient
![]() $(\mathfrak {g}_1^1)^i M / (\mathfrak {g}_1^1)^{i+1} M$
lies in BGG category
$(\mathfrak {g}_1^1)^i M / (\mathfrak {g}_1^1)^{i+1} M$
lies in BGG category
![]() $\mathcal {O}$
for
$\mathcal {O}$
for
![]() $\mathfrak {g}$
and hence has finite length, so this may be refined to a filtration satisfying (a) and (b).
$\mathfrak {g}$
and hence has finite length, so this may be refined to a filtration satisfying (a) and (b).
For
![]() $n> 1$
, consider the filtration
$n> 1$
, consider the filtration
![]() $M \supseteq \mathfrak {g}_{n}^n M \supseteq (\mathfrak {g}_{n}^n)^2 M \supseteq \cdots $
. Each quotient
$M \supseteq \mathfrak {g}_{n}^n M \supseteq (\mathfrak {g}_{n}^n)^2 M \supseteq \cdots $
. Each quotient
![]() $(\mathfrak {g}_n^n)^i M / (\mathfrak {g}_n^n)^{i+1} M$
lies in the category
$(\mathfrak {g}_n^n)^i M / (\mathfrak {g}_n^n)^{i+1} M$
lies in the category
![]() $\mathcal {O}^{(\mu )}(\mathfrak {g}_{n-1})$
, where we identify
$\mathcal {O}^{(\mu )}(\mathfrak {g}_{n-1})$
, where we identify
![]() $\mu $
with an element of
$\mu $
with an element of
![]() $(\mathfrak {h}_{n-1}^{\ge 1})^{*}$
in the obvious manner, so we may set
$(\mathfrak {h}_{n-1}^{\ge 1})^{*}$
in the obvious manner, so we may set
![]() $M_{(i, 0, \dots , 0)} = (\mathfrak {g}_{n}^n)^i M$
and argue by induction that this may be refined to a filtration satisfying (a) and (b).
$M_{(i, 0, \dots , 0)} = (\mathfrak {g}_{n}^n)^i M$
and argue by induction that this may be refined to a filtration satisfying (a) and (b).
To show this filtration satisfies (c), it is enough to show that whenever
![]() $\mu (\mathfrak {h}_n^n) = 0$
, every
$\mu (\mathfrak {h}_n^n) = 0$
, every
![]() $M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
has the property that
$M \in \mathcal {O}^{(\mu )}(\mathfrak {g}_n)$
has the property that
![]() $\bigcap _{i \geq 0} (\mathfrak {g}_{n}^n)^i M = 0$
. By considering weight spaces, this property is preserved by taking quotients and extensions, so it is enough to verify this in the case where
$\bigcap _{i \geq 0} (\mathfrak {g}_{n}^n)^i M = 0$
. By considering weight spaces, this property is preserved by taking quotients and extensions, so it is enough to verify this in the case where
![]() $M = M_{\lambda }$
is a Verma module. Since
$M = M_{\lambda }$
is a Verma module. Since
![]() $\lambda _n = \mu _n = 0$
, this Verma module is graded: we place a grading on
$\lambda _n = \mu _n = 0$
, this Verma module is graded: we place a grading on
![]() $U(\mathfrak {g}_n)$
by setting, for
$U(\mathfrak {g}_n)$
by setting, for
![]() $x\in \mathfrak {g}$
,
$x\in \mathfrak {g}$
,
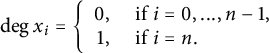 $$ \begin{align*} \deg x_{i} = \left\{ \begin{array}{rl} 0, & \text{ if } i=0,...,n-1,\\ 1, & \text{ if } i =n. \end{array} \right. \end{align*} $$
$$ \begin{align*} \deg x_{i} = \left\{ \begin{array}{rl} 0, & \text{ if } i=0,...,n-1,\\ 1, & \text{ if } i =n. \end{array} \right. \end{align*} $$
We transfer the induced grading on
![]() $U(\mathfrak {n}^-_n)$
to
$U(\mathfrak {n}^-_n)$
to
![]() $M_\lambda $
via the isomorphism of
$M_\lambda $
via the isomorphism of
![]() $\mathfrak {n}^-_n$
-modules
$\mathfrak {n}^-_n$
-modules
![]() $U(\mathfrak {n}^-_n) \cong M_\lambda $
. Now,
$U(\mathfrak {n}^-_n) \cong M_\lambda $
. Now,
![]() $M_\lambda $
is a positively graded
$M_\lambda $
is a positively graded
![]() $\mathfrak {g}_n$
-module and
$\mathfrak {g}_n$
-module and
![]() $\bigcap _{i \geq 0} (\mathfrak {g}_{n}^n)^i M_\lambda $
is contained in the intersection of all graded components, which is zero.
$\bigcap _{i \geq 0} (\mathfrak {g}_{n}^n)^i M_\lambda $
is contained in the intersection of all graded components, which is zero.
Finally, we observe that
![]() $\operatorname {ch}(M) = \sum _{(i_0, \dots , i_n) \in \mathcal {I}, i_n> 0} \operatorname {ch} (M_{i_0, \dots , i_n - 1}/ M_{i_0, \dots , i_n})$
, so by uniqueness in Lemma 6.1, the final part of the lemma holds.
$\operatorname {ch}(M) = \sum _{(i_0, \dots , i_n) \in \mathcal {I}, i_n> 0} \operatorname {ch} (M_{i_0, \dots , i_n - 1}/ M_{i_0, \dots , i_n})$
, so by uniqueness in Lemma 6.1, the final part of the lemma holds.
This result justifies the use of the terminology composition multiplicities, for
![]() $k_\lambda (M)$
. From now on, we use the notation
$k_\lambda (M)$
. From now on, we use the notation
![]() $[M : L_{\lambda }] := k_\lambda (M)$
.
$[M : L_{\lambda }] := k_\lambda (M)$
.
Corollary 6.3 The parabolic induction and restriction functors and the twisting functors
![]() $T_{\alpha }, G_{\alpha }$
preserve composition multiplicities.
$T_{\alpha }, G_{\alpha }$
preserve composition multiplicities.
Proof The proof is the same as [Reference ChaffeCh23, Corollary 6.3].
6.2 Computation of composition multiplicities for Verma modules
We now wish to compute the composition multiplicities
![]() $[M_\lambda : L_\nu ]$
. Thanks to Lemmas 3.4 and 6.2, we know that
$[M_\lambda : L_\nu ]$
. Thanks to Lemmas 3.4 and 6.2, we know that
![]() $[M_\lambda : L_\nu ] = 0$
unless
$[M_\lambda : L_\nu ] = 0$
unless
![]() $\lambda _n = \nu _n$
and so, using a combination of twisting functors and parabolic induction functors, we can reduce to the case
$\lambda _n = \nu _n$
and so, using a combination of twisting functors and parabolic induction functors, we can reduce to the case
![]() $\lambda _n = \nu _n = 0$
, and this is our strategy.
$\lambda _n = \nu _n = 0$
, and this is our strategy.
Let
![]() $p : \mathbb {Z}_{\ge 0} \Phi ^+ \to \mathbb {Z}_{\ge 0}$
be Kostant’s partition function. For
$p : \mathbb {Z}_{\ge 0} \Phi ^+ \to \mathbb {Z}_{\ge 0}$
be Kostant’s partition function. For
![]() $\alpha \in \mathbb {Z} \Phi $
, we write
$\alpha \in \mathbb {Z} \Phi $
, we write
![]() $\alpha _0 \in \mathfrak {h}_{n-1}^{*}$
to be the element satisfying
$\alpha _0 \in \mathfrak {h}_{n-1}^{*}$
to be the element satisfying
![]() $\alpha _0(h_i) = 0$
for
$\alpha _0(h_i) = 0$
for
![]() $i> 0$
and
$i> 0$
and
![]() $\alpha _0(h_0) = \alpha (h)$
, where
$\alpha _0(h_0) = \alpha (h)$
, where
![]() $h\in \mathfrak {h}$
. Also, for any
$h\in \mathfrak {h}$
. Also, for any
![]() $\lambda \in \mathfrak {h}_n^{*}$
, we identify
$\lambda \in \mathfrak {h}_n^{*}$
, we identify
![]() $\lambda _{\le n-1}$
with an element of
$\lambda _{\le n-1}$
with an element of
![]() $\mathfrak {h}_{n-1}^{*}$
in the obvious manner.
$\mathfrak {h}_{n-1}^{*}$
in the obvious manner.
Lemma 6.4 If
![]() $M_{\lambda _{\le n-1} - \alpha _0}(\mathfrak {g}_{n-1})$
is the Verma module over
$M_{\lambda _{\le n-1} - \alpha _0}(\mathfrak {g}_{n-1})$
is the Verma module over
![]() $\mathfrak {g}_{n-1}$
, then
$\mathfrak {g}_{n-1}$
, then
Proof Note that characters can be defined for any semisimple
![]() $\mathfrak {h}$
-module with finite-dimensional weight spaces. Let
$\mathfrak {h}$
-module with finite-dimensional weight spaces. Let
![]() $\mathbb {C}_{\lambda _0}$
be the
$\mathbb {C}_{\lambda _0}$
be the
![]() $\mathfrak {h}$
-module of weight
$\mathfrak {h}$
-module of weight
![]() $\lambda _0$
.
$\lambda _0$
.
Since
![]() $M_\lambda \cong U(\mathfrak {n}^-_n) \otimes \mathbb {C}_{\lambda _0}$
as
$M_\lambda \cong U(\mathfrak {n}^-_n) \otimes \mathbb {C}_{\lambda _0}$
as
![]() $\mathfrak {h}$
-modules, the lemma follows from the facts:
$\mathfrak {h}$
-modules, the lemma follows from the facts:
-
(i) The character of
 $U(\mathfrak {n}^-_n)$
is equal to the character of
$U(\mathfrak {n}^-_n)$
is equal to the character of
 $S(\mathfrak {n}^-_n)$
.
$S(\mathfrak {n}^-_n)$
. -
(ii)
 $S(\mathfrak {n}^-_n)$
is a free module over
$S(\mathfrak {n}^-_n)$
is a free module over
 $S(\mathfrak {n}^-_{n-1})$
and, for
$S(\mathfrak {n}^-_{n-1})$
and, for
 $\alpha \in \mathbb {Z}_{\ge 0} \Phi ^+$
, there are
$\alpha \in \mathbb {Z}_{\ge 0} \Phi ^+$
, there are
 $p(\alpha )$
basis vectors of weight
$p(\alpha )$
basis vectors of weight
 $-\alpha $
.
$-\alpha $
.
Corollary 6.5 If
![]() $\lambda , \nu \in \mathfrak {h}_n^{*}$
satisfy
$\lambda , \nu \in \mathfrak {h}_n^{*}$
satisfy
![]() $\lambda _n = \nu _n = 0$
,
$\lambda _n = \nu _n = 0$
,
![]() $\lambda _{\ge 1} = \nu _{\ge 1}$
, and
$\lambda _{\ge 1} = \nu _{\ge 1}$
, and
![]() $L_{\nu _{\le n-1}}(\mathfrak {g}_{n-1})$
denotes the simple
$L_{\nu _{\le n-1}}(\mathfrak {g}_{n-1})$
denotes the simple
![]() $\mathfrak {g}_{n-1}$
-module of highest weight
$\mathfrak {g}_{n-1}$
-module of highest weight
![]() $\nu _{\leq n-1}\in \mathfrak {h}_n^{*}$
, then
$\nu _{\leq n-1}\in \mathfrak {h}_n^{*}$
, then
Proof By Lemma 3.6, we have
![]() $\operatorname {ch} L_{\nu } = \operatorname {ch} L_{\nu _{\le n-1}}$
for all
$\operatorname {ch} L_{\nu } = \operatorname {ch} L_{\nu _{\le n-1}}$
for all
![]() $\nu \in \mathfrak {h}_n^{*}$
satisfying
$\nu \in \mathfrak {h}_n^{*}$
satisfying
![]() $\nu _n = 0$
, and so the claim follows from Lemma 6.4.
$\nu _n = 0$
, and so the claim follows from Lemma 6.4.
For
![]() $\mu _n \in \mathfrak {h}^{*}$
, we write
$\mu _n \in \mathfrak {h}^{*}$
, we write
![]() $\mathfrak {g}^{\mu _n}_{n-1} := (\mathfrak {g}^{\mu _n})_{n-1} = (\mathfrak {g}_{n-1})^{\mu _n}$
.
$\mathfrak {g}^{\mu _n}_{n-1} := (\mathfrak {g}^{\mu _n})_{n-1} = (\mathfrak {g}_{n-1})^{\mu _n}$
.
Corollary 6.6 Let
![]() $\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
such that
$\mu \in (\mathfrak {h}_n^{\ge 1})^{*}$
such that
![]() $\mathfrak {g}^{\mu _n}$
is the Levi factor of a standard parabolic. Then, for any
$\mathfrak {g}^{\mu _n}$
is the Levi factor of a standard parabolic. Then, for any
![]() $\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
$\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
![]() $\lambda _{\ge 1} = \nu _{\ge 1} = \mu $
, we have
$\lambda _{\ge 1} = \nu _{\ge 1} = \mu $
, we have
Proof This follows from Lemma 3.7, Theorem 4.1, and Corollaries 6.2 and 6.5. In order to apply these results, one should check that the functors appearing in the first two cited results send highest weight modules to highest weight modules of the corresponding weight, and we leave this verification to the reader.
To complete the computation of composition multiplicities for all Verma modules, we must show that to any Jordan block, we can apply twisting functors to obtain a Jordan block
![]() $\mathcal {O}^{(\mu )}$
such that
$\mathcal {O}^{(\mu )}$
such that
![]() $\mathfrak {g}^\mu $
is the Levi factor of a standard parabolic. This is possible thanks to the following result (see [Reference ChaffeCh23, Lemma 2.1] for a proof).
$\mathfrak {g}^\mu $
is the Levi factor of a standard parabolic. This is possible thanks to the following result (see [Reference ChaffeCh23, Lemma 2.1] for a proof).
Proposition 6.7 Let
![]() $\mu \in \mathfrak {h}^{*}$
. Then there exist
$\mu \in \mathfrak {h}^{*}$
. Then there exist
![]() $w \in W$
and a Levi factor
$w \in W$
and a Levi factor
![]() $\mathfrak {l}$
of a standard parabolic
$\mathfrak {l}$
of a standard parabolic
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\mathfrak {g}^{w(\mu )} = \mathfrak {l}$
. Furthermore, if w is chosen to be of minimal length subject to this condition and
$\mathfrak {g}^{w(\mu )} = \mathfrak {l}$
. Furthermore, if w is chosen to be of minimal length subject to this condition and
![]() $w = s_{\alpha _n} s_{\alpha _{n-1}} \dots s_{\alpha _1}$
is a reduced expression for w, then for each
$w = s_{\alpha _n} s_{\alpha _{n-1}} \dots s_{\alpha _1}$
is a reduced expression for w, then for each
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $((s_{\alpha _{i-1}} \dots s_{\alpha _1})\mu )(h_{\alpha _i}) \neq 0$
.
$((s_{\alpha _{i-1}} \dots s_{\alpha _1})\mu )(h_{\alpha _i}) \neq 0$
.
We now define an action
![]() $\bullet_{n}$
of W on
$\bullet_{n}$
of W on
![]() $\mathfrak {h}^{*}$
by
$\mathfrak {h}^{*}$
by
![]() $w \bullet_{n} \lambda := w(\lambda + n\rho ) - n\rho $
where
$w \bullet_{n} \lambda := w(\lambda + n\rho ) - n\rho $
where
![]() $\rho $
is half the sum of the positive roots. Note that this generalizes the dot action of W on
$\rho $
is half the sum of the positive roots. Note that this generalizes the dot action of W on
![]() $\mathfrak {h}^{*}$
, which corresponds to the case
$\mathfrak {h}^{*}$
, which corresponds to the case
![]() $n=1$
, and which controls the central characters of
$n=1$
, and which controls the central characters of
![]() $\mathfrak {g}_0$
[Reference HumphreysHu08, Section 1.9]. We remark that this n-dot action appeared in the work of Geoffriau on the center of the enveloping algebra of
$\mathfrak {g}_0$
[Reference HumphreysHu08, Section 1.9]. We remark that this n-dot action appeared in the work of Geoffriau on the center of the enveloping algebra of
![]() $\mathfrak {g}_n$
[Reference GeoffriauGe95].
$\mathfrak {g}_n$
[Reference GeoffriauGe95].
If
![]() $\alpha $
is any simple root, then since
$\alpha $
is any simple root, then since
![]() $s_{\alpha }(\alpha ) = -\alpha $
and
$s_{\alpha }(\alpha ) = -\alpha $
and
![]() $s_{\alpha }$
permutes the other positive roots, we have
$s_{\alpha }$
permutes the other positive roots, we have
![]() $s_{\alpha }(\rho ) = \rho - \alpha $
. We then have
$s_{\alpha }(\rho ) = \rho - \alpha $
. We then have
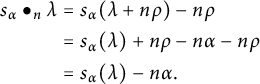 $$ \begin{align*} s_{\alpha} \bullet_{n} \lambda &= s_{\alpha}(\lambda + n\rho) - n\rho \\ &= s_{\alpha}(\lambda) + n\rho - n\alpha - n\rho \\ &= s_{\alpha}(\lambda) - n\alpha. \end{align*} $$
$$ \begin{align*} s_{\alpha} \bullet_{n} \lambda &= s_{\alpha}(\lambda + n\rho) - n\rho \\ &= s_{\alpha}(\lambda) + n\rho - n\alpha - n\rho \\ &= s_{\alpha}(\lambda) - n\alpha. \end{align*} $$
We extend this to a W-action on
![]() $\mathfrak {h}_n^{*}$
by setting
$\mathfrak {h}_n^{*}$
by setting
 $$ \begin{align*} (s_{\alpha} \bullet_{n} \lambda)(h_i) = \left\{\begin{array}{@{}cc} (s_{\alpha}\bullet_{n} \lambda_i) (h_i), & \text{ for } i = 0, \\ (s_{\alpha} \lambda_{i})(h_{i}), &\text{ for } i \ne 0. \end{array} \right. \end{align*} $$
$$ \begin{align*} (s_{\alpha} \bullet_{n} \lambda)(h_i) = \left\{\begin{array}{@{}cc} (s_{\alpha}\bullet_{n} \lambda_i) (h_i), & \text{ for } i = 0, \\ (s_{\alpha} \lambda_{i})(h_{i}), &\text{ for } i \ne 0. \end{array} \right. \end{align*} $$
By our calculations in the proof of Lemma 5.10, the twisting functors
![]() $T_{\alpha }$
take highest weight modules of weight
$T_{\alpha }$
take highest weight modules of weight
![]() $\lambda \in \mathfrak {h}_n^{*}$
to highest weight modules of weight
$\lambda \in \mathfrak {h}_n^{*}$
to highest weight modules of weight
![]() $s_{\alpha } \bullet_{n} \lambda $
, and hence take
$s_{\alpha } \bullet_{n} \lambda $
, and hence take
![]() $M_{\lambda }$
to
$M_{\lambda }$
to
![]() $M_{s_{\alpha } \bullet_{n} \lambda }$
and similar for
$M_{s_{\alpha } \bullet_{n} \lambda }$
and similar for
![]() $L_{\lambda }$
. Applying Corollary 6.3 again, we obtain the following.
$L_{\lambda }$
. Applying Corollary 6.3 again, we obtain the following.
Corollary 6.8 Let
![]() $\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
$\lambda , \nu \in \mathfrak {h}_n^{*}$
such that
![]() $\lambda _{\ge 1} = \nu _{\ge 1}$
. Let
$\lambda _{\ge 1} = \nu _{\ge 1}$
. Let
![]() $w \in W$
have a reduced expression
$w \in W$
have a reduced expression
![]() $w = s_{\alpha _k} s_{\alpha _{k-1}} \cdots s_{\alpha _1}$
for simple reflections
$w = s_{\alpha _k} s_{\alpha _{k-1}} \cdots s_{\alpha _1}$
for simple reflections
![]() $s_{\alpha _i}$
such that:
$s_{\alpha _i}$
such that:
-
(a)
 $\mathfrak {g}^{w(\mu _n)}$
is the Levi factor of a standard parabolic.
$\mathfrak {g}^{w(\mu _n)}$
is the Levi factor of a standard parabolic. -
(b) For each
 $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
 $((s_{\alpha _{i-1}} \cdots s_{\alpha _1})\mu )(h_{\alpha _i}) \neq 0$
.
$((s_{\alpha _{i-1}} \cdots s_{\alpha _1})\mu )(h_{\alpha _i}) \neq 0$
.
Then we have
 $$ \begin{align} [M_{\lambda}: L_{\nu}] &= [M_{w \bullet_{n} \lambda}: L_{w \bullet_{n} \nu}]\nonumber\\ &= \sum_{\alpha \in \mathbb{Z}_{\ge 0}\Phi^+} p(\alpha) [M_{(w \bullet_{n} \lambda)_{\leq n-1} -\alpha_0}(\mathfrak{g}^{w(\lambda_n)}_{n-1}): L_{(w \bullet_{n} \nu)_{\leq n-1}}(\mathfrak{g}^{w(\mu_n)}_{n-1})]. \end{align} $$
$$ \begin{align} [M_{\lambda}: L_{\nu}] &= [M_{w \bullet_{n} \lambda}: L_{w \bullet_{n} \nu}]\nonumber\\ &= \sum_{\alpha \in \mathbb{Z}_{\ge 0}\Phi^+} p(\alpha) [M_{(w \bullet_{n} \lambda)_{\leq n-1} -\alpha_0}(\mathfrak{g}^{w(\lambda_n)}_{n-1}): L_{(w \bullet_{n} \nu)_{\leq n-1}}(\mathfrak{g}^{w(\mu_n)}_{n-1})]. \end{align} $$
Acknowledgment
Both authors would like to thank Simon Goodwin for many useful conversations.