Article contents
The Central Limit Theorem for Subsequences in Probabilistic Number Theory
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 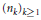 ${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ be an increasing sequence of positive integers, and let
${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ be an increasing sequence of positive integers, and let 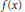 $f\left( x \right)$ be a real function satisfying
$f\left( x \right)$ be a real function satisfying
1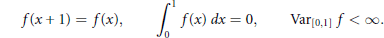 $$f\left( x+1 \right)=f\left( x \right),\int\limits_{0}^{1}{f\left( x \right)}dx=0,\text{Va}{{\text{r}}_{\left[ 0,1 \right]}}f<\infty $$
$$f\left( x+1 \right)=f\left( x \right),\int\limits_{0}^{1}{f\left( x \right)}dx=0,\text{Va}{{\text{r}}_{\left[ 0,1 \right]}}f<\infty $$
If 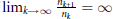 ${{\lim }_{k\to \infty }}\frac{{{n}_{k+1}}}{{{n}_{k}}}=\infty $ the distribution of
${{\lim }_{k\to \infty }}\frac{{{n}_{k+1}}}{{{n}_{k}}}=\infty $ the distribution of
2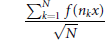 $$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{n}_{k}}x \right)}}{\sqrt{N}}$$
$$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{n}_{k}}x \right)}}{\sqrt{N}}$$
converges to a Gaussian distribution. In the case
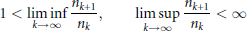 $$1<\underset{k\to \infty }{\mathop{\lim \inf }}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}},\,\,\underset{k\to \infty }{\mathop{\text{lim}\,\text{sup}}}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}}<\infty$$
$$1<\underset{k\to \infty }{\mathop{\lim \inf }}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}},\,\,\underset{k\to \infty }{\mathop{\text{lim}\,\text{sup}}}\,\,\frac{{{n}_{k+1}}}{{{n}_{k}}}<\infty$$
there is a complex interplay between the analytic properties of the function 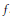 $f$ , the number-theoretic properties of
$f$ , the number-theoretic properties of 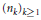 ${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ , and the limit distribution of (2).
${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ , and the limit distribution of (2).
In this paper we prove that any sequence 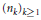 ${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying
${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying 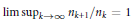 $\lim {{\sup }_{k\to \infty }}{{n}_{k+1}}/{{n}_{k}}=1$ contains a nontrivial subsequence
$\lim {{\sup }_{k\to \infty }}{{n}_{k+1}}/{{n}_{k}}=1$ contains a nontrivial subsequence 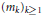 ${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ such that for any function satisfying (1) the distribution of
${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ such that for any function satisfying (1) the distribution of
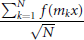 $$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{m}_{k}}x \right)}}{\sqrt{N}}$$
$$\frac{\sum\nolimits_{k=1}^{N}{f\left( {{m}_{k}}x \right)}}{\sqrt{N}}$$
converges to a Gaussian distribution. This result is best possible: for any 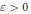 $\varepsilon >0$ there exists a sequence
$\varepsilon >0$ there exists a sequence 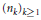 ${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying lim
${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ satisfying lim 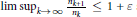 $\underset{k\to \infty }{\mathop{\sup }}\,\frac{{{n}_{k+1}}}{{{n}_{k}}}\le 1+\varepsilon$ such that for every nontrivial subsequence
$\underset{k\to \infty }{\mathop{\sup }}\,\frac{{{n}_{k+1}}}{{{n}_{k}}}\le 1+\varepsilon$ such that for every nontrivial subsequence 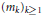 ${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ of
${{\left( {{m}_{k}} \right)}_{k\ge 1}}$ of 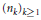 ${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ the distribution of (2) does not converge to a Gaussian distribution for some
${{\left( {{n}_{k}} \right)}_{k\ge 1}}$ the distribution of (2) does not converge to a Gaussian distribution for some 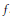 $f$ .
$f$ .
Our result can be viewed as a Ramsey type result: a sufficiently dense increasing integer sequence contains a subsequence having a certain requested number-theoretic property.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012
References
- 2
- Cited by

