Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tan, Shaobin
1999.
TKK algebras and vertex operator representations.
Journal of Algebra,
Vol. 211,
Issue. 1,
p.
298.
Faulkner, John R
2000.
Jordan Pairs and Hopf Algebras.
Journal of Algebra,
Vol. 232,
Issue. 1,
p.
152.
Liu, Dong
and
Hu, Naihong
2005.
Steinberg unitary Leibniz algebras.
Linear Algebra and its Applications,
Vol. 405,
Issue. ,
p.
279.
Liu, Dong
2005.
Steinberg–Leibniz algebras and superalgebras.
Journal of Algebra,
Vol. 283,
Issue. 1,
p.
199.
Liu, Dong
and
Hu, Naihong
2007.
Universal Central Extensions of the Matrix Leibniz Superalgebras 𝔰𝔩(m,n, 𝒜).
Communications in Algebra,
Vol. 35,
Issue. 6,
p.
1814.
Mao, Xinhui
and
Tan, Shaobin
2007.
Vertex operator representations for TKK algebras.
Journal of Algebra,
Vol. 308,
Issue. 2,
p.
704.
Smirnov, O.N.
2011.
Imbedding of Lie triple systems into Lie algebras.
Journal of Algebra,
Vol. 341,
Issue. 1,
p.
1.
Chang, Zhihua
Gao, Yun
and
Zheng, Yelong
2013.
Finite dimensional irreducible representations of elementary unitary Lie algebras over quantum tori.
Journal of Algebra,
Vol. 395,
Issue. ,
p.
1.
Caveny, D. M.
and
Smirnov, O. N.
2014.
Categories of Jordan Structures and Graded Lie Algebras.
Communications in Algebra,
Vol. 42,
Issue. 1,
p.
186.
Zhang, Zezhou
2021.
Finite presentability of universal central extensions of sln, II.
Journal of Algebra,
Vol. 573,
Issue. ,
p.
169.
Kashuba, Iryna
and
Mathieu, Olivier
2021.
On the free Jordan algebras.
Advances in Mathematics,
Vol. 383,
Issue. ,
p.
107690.
Murakami, L. S. I.
Peresi, L. A.
and
Shestakov, I. P.
2022.
A retrospect of the research in nonassociative algebras in IME-USP.
São Paulo Journal of Mathematical Sciences,
Vol. 16,
Issue. 1,
p.
84.
Shang, Shikui
2025.
The Z2-graded dimensions of the free Jordan superalgebra J(D1|D2).
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 2,
p.
107879.
Dotsenko, Vladimir
and
Kashuba, Iryna
2025.
The three graces in the Tits–Kantor–Koecher
category.
Orbita Mathematicae,
Vol. 2,
Issue. 1,
p.
83.


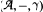 , where
, where 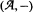 is a unital nonassociative algebra with involution and
is a unital nonassociative algebra with involution and 