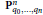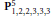Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Yunfeng
2008.
The orbifold cohomology ring of simplicial toric stack bundles.
Illinois Journal of Mathematics,
Vol. 52,
Issue. 2,
Coates, Tom
Corti, Alessio
Lee, Yuan-Pin
and
Tseng, Hsian-Hua
2009.
The quantum orbifold cohomology of weighted projective spaces.
Acta Mathematica,
Vol. 202,
Issue. 2,
p.
139.
Boissière, Samuel
Mann, Étienne
and
Perroni, Fabio
2009.
A Model for the Orbifold Chow Ring of Weighted Projective Spaces.
Communications in Algebra,
Vol. 37,
Issue. 2,
p.
503.
Ding, Fan
Jiang, Yun Feng
and
Pan, Jian Zhong
2010.
The Chen-Ruan cohomology of almost contact orbifolds.
Acta Mathematica Sinica, English Series,
Vol. 26,
Issue. 1,
p.
77.
Goldin, Rebecca
Harada, Megumi
Johannsen, David
and
Krepski, Derek
2016.
Inertia groups of a toric Deligne-Mumford stack, fake weighted projective stacks, and labeled sheared simplices.
Rocky Mountain Journal of Mathematics,
Vol. 46,
Issue. 2,
Li, Ti Yao
and
Chen, Bo Hui
2016.
Hamiltonian Gromov–Witten invariants on ℂ n+1 with S 1-action.
Acta Mathematica Sinica, English Series,
Vol. 32,
Issue. 3,
p.
309.
Farsi, Carla
and
Seaton, Christopher
2017.
Functional equations for orbifold wreath products.
Journal of Geometry and Physics,
Vol. 120,
Issue. ,
p.
37.
Konishi, Yukiko
and
Minabe, Satoshi
2020.
Mixed Frobenius structure and the local A-model.
Kyoto Journal of Mathematics,
Vol. 60,
Issue. 3,