Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-30T09:24:35.091Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of homomorphisms from 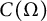$C(\Omega)$ to a 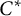$C^*$-algebra

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  21 April 2025

Qingnan An ,
George Arthur Elliott  and
Zhichao Liu Open the ORCID record for Zhichao Liu [Opens in a new window]
Qingnan An
Affiliation:
School of Mathematics and Statistics, Northeast Normal University, Changchun, China e-mail: qingnanan1024@outlook.com
George Arthur Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, Canada e-mail: elliott@math.toronto.edu
Zhichao Liu*
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian, China
*
e-mail: lzc.12@outlook.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\Omega $ be a compact subset of 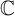$\mathbb {C}$ and let A be a unital simple, separable 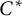$C^*$-algebra with stable rank one, real rank zero, and strict comparison. We show that, given a Cu-morphism 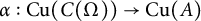${\alpha :\mathrm { Cu}(C(\Omega ))\to \mathrm {Cu}(A)}$ with 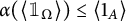, there exists a homomorphism 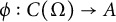$\phi : C(\Omega )\to A$ such that 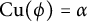$\mathrm {Cu}(\phi )=\alpha $. Moreover, if 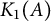$K_1(A)$ is trivial, then $\phi $ is unique up to approximate unitary equivalence. We also give classification results for maps from a large class of 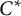$C^*$-algebras to A in terms of the Cuntz semigroup.

Keywords

ClassificationCuntz semigroupstrict comparison

MSC classification

Primary: 46L35: Classifications of $C^*$-algebras 46L05: General theory of $C^*$-algebras

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The research of the first author was supported by NNSF of China (Grant No.: 12101113). The research of the second author was supported by NSERC of Canada. The third author was supported by LiaoNing Revitalization Talents Program (No.: XLYC2403058) and NNSF of China (Grant No.: 12101102).

References

Allen, H., Algebraic topology. Cambridge University Press, Cambridge, 2002, xii+544 pp.Google Scholar
Antoine, R., Perera, F., and Thiel, H., Tensor products and regularity properties of Cuntz semigroups . Mem. Amer. Math. Soc. 251(2018), no. 1199, viii+191 pp.Google Scholar
Blanchard, E. and Kirchberg, E., Non-simple purely infinite ${C}^{\ast }$ -algebras: the Hausdorff case . J. Funct. Anal. 207(2004), 461–513.10.1016/j.jfa.2003.06.008CrossRefGoogle Scholar
Blackadar, B. and Handelman, D., Dimension functions and traces on ${C}^{\ast }$ -algebras . J. Funct. Anal. 45(1982), no. 3, 297–340.10.1016/0022-1236(82)90009-XCrossRefGoogle Scholar
Brown, L. G., Stable isomorphism of hereditary subalgebras of ${C}^{\ast }$ -algebras . Pacific J. Math. 71(1977), no. 2, 335–348.CrossRefGoogle Scholar
Brown, N. P., Perera, F., and Toms, A. S., The Cuntz semigroup, the Elliott conjecture, and dimension functions on ${C}^{\ast }$ -algebras . J. Reine Angew. Math. 621(2008), 191–211.Google Scholar
Brown, N. P. and Winter, W., Quasitraces are traces: A short proof of the finite-nuclear-dimension case . C. R. Math. Acad. Sci. Soc. R. Can. 33(2011), no. 2, 44–49.Google Scholar
Cantier, L., Towards a classification of unitary elements of ${C}^{\ast }$ -algebras. Int. Math. Res. Not. IMRN (2025), no. 7, rnaf068.Google Scholar
Cantier, L. and Vilalta, E., Fraïssé Theory for Cuntz semigroups . J. Algebra 658(2024), 319–364.10.1016/j.jalgebra.2024.05.052CrossRefGoogle Scholar
Ciuperca, A. and Elliott, G. A., A remark on invariants for ${C}^{\ast }$ -algebras of stable rank one . Int. Math. Res. Not. IMRN 158(2008), no. 5, Art. ID rnm158, 33pp.Google Scholar
Ciuperca, A., Elliott, G. A., and Santiago, L., On inductive limits of type-I ${C}^{\ast }$ -algebras with one-dimensional spectrum . Int. Math. Res. Not. IMRN (2011), no. 11, 2577–2615.Google Scholar
Coward, K. T., Elliott, G. A., and Ivanescu, C., The Cuntz semigroup as an invariant for ${C}^{\ast }$ -algebras . J. Reine Angew. Math. 623(2008), 161–193.Google Scholar
Cuntz, J., Dimension functions on simple ${C}^{\ast }$ -algebras . Math. Ann. 233(1978), no. 2, 145–153.10.1007/BF01421922CrossRefGoogle Scholar
Dadarlat, M. and Toms, A. S., Ranks of operators in simple ${C}^{\ast }$ -algebras . J. Funct. Anal. 259(2010), 1209–1229.10.1016/j.jfa.2010.03.022CrossRefGoogle Scholar
Elliott, G. A., Hilbert modules over ${C}^{\ast }$ -algebras of stable rank one . C. R. Math. Acad. Sci. Soc. R. Can. 29(2007), 48–51.Google Scholar
Elliott, G. A. and Liu, Z., Distance between unitary orbits in ${C}^{\ast }$ -algebras with stable rank one and real rank zero . J. Oper. Theory 86(2021), no. 2, 299–316.10.7900/jot.2020apr21.2306CrossRefGoogle Scholar
Elliott, G. A., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a ${C}^{\ast }$ -algebra . Amer. J. Math. 133(2011), no. 4, 969–1005.10.1353/ajm.2011.0027CrossRefGoogle Scholar
Fu, X. and Lin, H., Tracial oscillation zero and stable rank one . Canad. J. Math. 77(2025), no 2, 563–630.10.4153/S0008414X24000099CrossRefGoogle Scholar
Gardella, E. and Perera, F., The modern theory of Cuntz semigroups of ${C}^{\ast }$ -algebras. Preprint. arXiv:2212.02290v2.Google Scholar
Haagerup, U., Quasitraces on exact ${C}^{\ast }$ -algebras are traces . C. R. Math. Acad. Sci. Soc. R. Can. 36(2014), nos. 2–3, 67–92.Google Scholar
Hu, S. and Lin, H., Distance between unitary orbits of normal elements in simple ${C}^{\ast }$ -algebras of real rank zero . J. Funct. Anal. 269(2015), 903–907.10.1016/j.jfa.2015.02.006CrossRefGoogle Scholar
Jacelon, B., Strung, K. R., and Toms, A. S., Unitary orbits of self-adjoint operators in simple -stable ${C}^{\ast }$ -algebras . J. Funct. Anal. 269(2015), 3304–3315.10.1016/j.jfa.2015.08.019CrossRefGoogle Scholar
Jacelon, B., Strung, K. R., and Vignati, A., Optimal transport and unitary orbits in ${C}^{\ast }$ -algebras . J. Funct. Anal. 281(2021), no. 5, Paper No. 109068. 30 pp.10.1016/j.jfa.2021.109068CrossRefGoogle Scholar
Kaftal, V., Ng, P. W., and Zhang, S., Commutators and linear spans of projections in certain finite ${C}^{\ast }$ -algebras . J. Funct. Anal. 266(2014), no. 4, 1883–1912.10.1016/j.jfa.2013.12.009CrossRefGoogle Scholar
Ortega, E., Rørdam, M., and Thiel, H., The Cuntz semigroup and comparison of open projections . J. Funct. Anal. 260(2011), no. 12, 3474–3493.10.1016/j.jfa.2011.02.017CrossRefGoogle Scholar
Robert, L., Classification of inductive limits of 1-dimensional NCCW complexes . Adv. Math. 231(2012), 2802–2836.10.1016/j.aim.2012.07.010CrossRefGoogle Scholar
Robert, L., The Cuntz semigroup of some spaces of dimension at most two . C. R. Math. Acad. Sci. Soc. R. Can. 35(2013), 22–32.Google Scholar
Robert, L. and Santiago, L., Classification of ${C}^{\ast }$ -homomorphisms from ${C}_0\left(0,1\right]$ to a ${C}^{\ast }$ -algebra. J. Funct. Anal. 258(2010), no. 3, 869–892.10.1016/j.jfa.2009.06.025CrossRefGoogle Scholar
Rørdam, M., On the structure of simple ${C}^{\ast }$ -algebras tensored with a UHF-algebra, II . J. Funct. Anal. 107(1992), 255–269.10.1016/0022-1236(92)90106-SCrossRefGoogle Scholar
Rørdam, M., Larsen, F., and Laustsen, N. J., An introduction to K-theory for  ${C}^{\ast }$ -algebras, London Mathematical Society Student Texts, 49, Cambridge University Press, Cambridge, 2000. xii+242 pp.Google Scholar
Rørdam, M. and Winter, W., The Jiang–Su algebra revisited . J. Reine Angew. Math. 642(2010), 129–155.Google Scholar