Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-08T21:40:42.048Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactness of Commutators for Singular Integrals on Morrey Spaces

Published online by Cambridge University Press:  20 November 2018

Yanping Chen ,
Yong Ding  and
Xinxia Wang
Yanping Chen
Affiliation:
Department of Mathematics and Mechanics, Applied Science School, University of Science and Technology Beijing, Beijing 100083, P.R. China email: yanpingch@126.com
Yong Ding
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems (BNU), Ministry of Education, Beijing 100875, P.R. China email: dingy@bnu.edu.cn
Xinxia Wang
Affiliation:
The College of Mathematics and System Science, Xinjiang University, Urumqi, Xinjiang, 830046, P.R. China email: wxxa@xju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

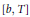In this paper we characterize the compactness of the commutator $\left[ b,\,T \right]$ for the singular integral operator on the Morrey spaces 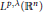${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$. More precisely, we prove that if 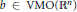$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$, the 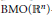$\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$-closure of 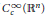$C_{c}^{\infty }\left( {{\mathbb{R}}^{n}} \right)$, then 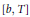$\left[ b,\,T \right]$ is a compact operator on the Morrey spaces 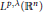${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for 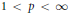$1\,<\,p\,<\,\infty $ and 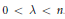$0\,<\,\lambda \,<\,n$. Conversely, if 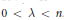$b\,\in \,\text{BMO}\left( {{\mathbb{R}}^{n}} \right)$ and 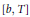$\left[ b,\,T \right]$ is a compact operator on the 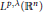${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ for some 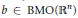$p\,\left( 1\,<\,p\,<\,\infty \right)$, then 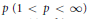$b\,\in \,\text{VMO}\left( {{\mathbb{R}}^{n}} \right)$. Moreover, the boundedness of a rough singular integral operator 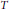$T$ and its commutator 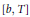$\left[ b,\,T \right]$ on 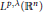${{L}^{p,\lambda }}\left( {{\mathbb{R}}^{n}} \right)$ are also given. We obtain a sufficient condition for a subset in Morrey space to be a strongly pre-compact set, which has interest in its own right.

Keywords

42B2042B99singular integralcommutatorscompactnessVMOMorrey space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 2 , 16 April 2012 , pp. 257 - 281
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Adams, D. R., A note on Riesz potentials. Duke Math J. 42(1975), no. 4, 765–778. http://dx.doi.org/10.1215/S0012-7094-75-04265-9 Google Scholar
[2] Adams, D. R. and Xiao, J. Nonlinear potential analysis on Morrey spaces and their capacities. Indiana Univ. Math. J. 53(2004), no. 6, 1629–1663.Google Scholar
[3] Adams, D. R. and Xiao, J., Morrey spaces in harmonic analysis. Ark. Mat. Published online March 4, 2011. http://dx.doi.org/10.1007/s11512-010-0134-0 Google Scholar
[4] Adams, D. R. and Xiao, J., Morrey potentials and harmonic maps. Comm. Math. Phys., to appear.Google Scholar
[5] Adams, D. R. and Xiao, J., Regularity of Morrey commutators. Trans. Amer. Math. Soc., to appear.Google Scholar
[6] Beatrous, F. and Li, S.-Y., Boundedness and compactness of operators of Hankel type. J. Funct. Anal. 111(1993), no. 2, 350–379. http://dx.doi.org/10.1006/jfan.1993.1017 Google Scholar
[7] Caffarelli, L., Elliptic second order equations. Rend. Sem. Mat. Fis. Milano 58(1988), 253–284. http://dx.doi.org/10.1007/BF02925245 Google Scholar
[8] Calderón, A.-P., Commutators, singular integrals on Lipschitz curves and applications. In: Proceedings of the International Congress of Mathematicians. Acad, Sci. Fennica, Helsinki, 1980, pp. 85–96.Google Scholar
[9] Calderón, A.-P. and Zygmund, A. On singular integrals. Amer. J. Math. 78(1956), 289–309. http://dx.doi.org/10.2307/2372517 Google Scholar
[10] Chen, Y. and Ding, Y. Compactness of the commutators of parabolic singular integrals. Sci. China Math. 53(2010), no. 10, 2633–2648. http://dx.doi.org/10.1007/s11425-010-4004-9 Google Scholar
[11] Chen, Y., Ding, Y. and Wang, X., Compactness of commutators of Riesz potential on Morrey space. Potential Anal. 30(2009), no. 4, 301–313. http://dx.doi.org/10.1007/s11118-008-9114-4 Google Scholar
[12] Chiarenza, F., Frasca, M. and Longo, P. Interior W2, p estimates for nondivergence elliptic equations with discontinuous coefficients. Ricerche Mat. 40(1991), no. 1, 149–168.Google Scholar
[13] Coifman, R., Lions, P. Meyer, Y. and Semmes, S. Compensated compactness and Hardy spaces. J. Math. Pures Appl. 72(1993), no. 3, 247–286.Google Scholar
[14] Coifman, R., Rochberg, R. and G.Weiss, Factorization theorems for Hardy spaces in several variables. Ann. of Math. 103(1976), no. 3, 611–635. http://dx.doi.org/10.2307/1970954 Google Scholar
[15] Deng, D., Duong, X. and Yan, L. A characterization of the Morrey-Campanato spaces. Math. Z. 250(2005), 641–655. http://dx.doi.org/10.1007/s00209-005-0769-x Google Scholar
[16] Ding, Y., A characterization of BMO via commutators for some operators. Northeastern Math. J. 13(1997), no. 4, 422–432.Google Scholar
[17] Ding, Y. and Lu, S. Homogeneous fractional integrals on Hardy spaces. Tôhoku Math. J. 52(2000), no. 1, 153–162. http://dx.doi.org/10.2748/tmj/1178224663 Google Scholar
[18] Di Fazio, G., Palagachev, D. and Ragusa, M. Global Morrey regularity of strong solutions to the Dirichlet problem for elliptic equations with discontinuous coefficients. J. Funct. Anal. 166(1999), no. 2, 179–196. http://dx.doi.org/10.1006/jfan.1999.3425 Google Scholar
[19] Di Fazio, G. and Ragusa, M. Commutators and Morrey spaces. Boll. Un. Mat. Ital. A 5(1991), no. 3, 323–332.Google Scholar
[20] Di Fazio, G. and Ragusa, M., Interior estimates in Morrey spaces for strong solutions to nondivergence form equations with discontinuous coefficients. J. Funct. Anal. 112(1993), no. 2, 241–256. http://dx.doi.org/10.1006/jfan.1993.1032 Google Scholar
[21] Duong, X., Xiao, J. and Yan, L. Old and new Morrey spaces via heat kernel bounds. J. Fourier Anal. Appl. 13(2007), no. 1, 87–111. http://dx.doi.org/10.1007/s00041-006-6057-2 Google Scholar
[22] Garćıa-Cuerva, J. and Rubio de, J. L. Francia, Weighted Norm Inequalities and Related Topics. North-Holland Mathematics Studies 116. North-Holland, Amsterdam, 1985.Google Scholar
[23] Hu, G., Lp(Rn) boundedness for the commutator of a homogeneous singular integral operator. Studia Math. 154(2003), no. 1, 13–27. http://dx.doi.org/10.4064/sm154-1-2 Google Scholar
[24] Huang, Q., Estimates on the generalized Morrey spaces L2, _ ’ and BMO for linear elliptic systems. Indiana Univ. Math. J. 45(1996), no. 2, 397–439.Google Scholar
[25] Iwaniec, T., Nonlinear commutators and Jacobians. J. Fourier Anal. Appl. 3(1997), Special Issue, 775–796. http://dx.doi.org/10.1007/BF02656485 Google Scholar
[26] Iwaniec, T. and Sboedone, C. Riesz treansform and elliptic PDE's with VMO-coefficients. J. Anal. Math. 74(1998), 183–212. http://dx.doi.org/10.1007/BF02819450 Google Scholar
[27] Janson, S., Mean oscillation and commutators of singular integral operators, Ark. Mat. 16(1978), no. 2, 263–270. http://dx.doi.org/10.1007/BF02386000 Google Scholar
[28] Kato, T., Strong solutions of the Navier-Stokes equation in Morrey spaces. Bol. Soc. Brasil. Mat. 22(1992), no. 2, 127–155. http://dx.doi.org/10.1007/BF01232939 Google Scholar
[29] Krantz, S. and Li, S.-Y., Boundedness and compactness of integral operators on spaces of homogeneous type and applications. I. II. J. Math. Anal. Appl. 258(2001), 629–641, 642–657. http://dx.doi.org/10.1006/jmaa.2000.7402 Google Scholar
[30] Lu, S., Ding, Y. and Yan, D. Singular Integral and Related Topics. World Scientific Publishing, Hackensack, NJ, 2007.Google Scholar
[31] Mazzucato, A., Besov-Morrey spaces: functions space theory and applications to non-linear PDE, Trans. Amer. Math. Soc. 355(2003), no. 4, 1297–1364. http://dx.doi.org/10.1090/S0002-9947-02-03214-2 Google Scholar
[32] Morrey, C., On the solutions of quasi-linear elleptic partial diferential equations. Trans. Amer. Math. Soc. 43(1938), no. 1, 126–166. http://dx.doi.org/10.1090/S0002-9947-1938-1501936-8 Google Scholar
[33] Mizuhara, T., Boundedness of some classical operators on generalized Morrey spaces. In: Harmonic Analysis. Springer, Tokyo, 1991, pp. 183–189.Google Scholar
[34] Nakai, E., Hardy-Littlewood maximal operator, singular integral operators and the Riesz potentials on generalized Morrey spaces. Math. Nachr. 166(1994), 95–103. http://dx.doi.org/10.1002/mana.19941660108 Google Scholar
[35] Palagachev, D. and Softova, L. Singular integral operators, Morrey spaces and fine regularity of solutions to PDE’s. Potential Anal. 20(2004), no. 3, 237–263. http://dx.doi.org/10.1023/B:POTA.0000010664.71807.f6 Google Scholar
[36] Pérez, C., Two weighted norm inequalities for Riesz potentials and uniform Lp-weighted Sobolev inequalities. Indiana Univ. Math. J. 39(1990), no. 1, 31–44. http://dx.doi.org/10.1512/iumj.1990.39.39004 Google Scholar
[37] Ruiz, A. and Vega, L. Unique continuation for Schrödinger operators with potential in Morrey spaces. Publ. Mat. 35(1991), no. 1, 291–298.Google Scholar
[38] Sawano, Y., Generalized Morrey spaces for non-doubling measures. No DEA Nonlinear Differential Equations Appl. 15(2008), no. 4-5, 413–425. http://dx.doi.org/10.1007/s00030-008-6032-5 Google Scholar
[39] Sawano, Y. and Shirai, S. Compact commtators on Morrey spaces with non-doubling measures. Georgian Math. J. 15(2008), no. 2, 353–376.Google Scholar
[40] Sawano, Y. and Tanaka, H. Morrey Spaces for non-doubling measures. Acta Math. Sin. (Engl. Ser.) 21(2005), no. 6, 1535–1544. http://dx.doi.org/10.1007/s10114-005-0660-z Google Scholar
[41] Sawano, Y. and Tanaka, H., Sharp maximal inequalities and commutators on Morrey spaces with non-doublin measueas. Taiwan. J. Math. 11(2007), no. 4, 1091–1112.Google Scholar
[42] Shen, Z., Boundary value problems in Morrey spaces for elliptic systems on Lipschitz domains. Amer. J. Math. 125(2003), no. 5, 1079–1115. http://dx.doi.org/10.1353/ajm.2003.0035 Google Scholar
[43] Shen, Z., The periodic Schrödinger operators with potentials in the Morrey class. J. Funct. Anal. 193(2002), no. 2, 314–345. http://dx.doi.org/10.1006/jfan.2001.3933 Google Scholar
[44] Softova, L., Singular integrals and commutators in generalized Morrey spaces. Acta Math. Sin. (Engl. Ser.) 22(2006), no. 3, 757–766. http://dx.doi.org/10.1007/s10114-005-0628-z Google Scholar
[45] Stein, E. M., Harmonic Analysis: Real Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton Mathematical Series 43. Princeton University Press, Princeton, NJ, 1993.Google Scholar
[46] Stein, E. M. and G.Weiss, Introduction to Fourier Analysis on Euclidean Spaces. Princeton Mathematical Series 32. Princeton University Press, Princeton, NJ, 1971.Google Scholar
[47] Taylor, M., Analysis on Morrey spaces and applications to Navier-Stokes and other evolution equations. Comm. Partial Differential Equations 17(1992). 1407–1456. http://dx.doi.org/10.1080/03605309208820892 Google Scholar
[48] Uchiyama, A., On the compactness of operators of Hankel type. Tôhoku Math. J. 30(1978), no. 1, 163–171. http://dx.doi.org/10.2748/tmj/1178230105 Google Scholar
[49] Yan, L., Classes of Hardy spaces associated with operators, duality theorem and applications. Trans. Amer. Math. Soc. 360(2008), no. 8, 4383–4408. http://dx.doi.org/10.1090/S0002-9947-08-04476-0 Google Scholar
[50] Yosida, K., Functional Analysis. Fifth edition. Grundlehren der Mathematischen Wissenschaften 123. Springer-Verlag, Berlin, 1978.Google Scholar