Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bousquet-Mélou, Mireille
Chapuy, Guillaume
and
Préville-Ratelle, Louis-François
2013.
The representation of the symmetric group on m -Tamari intervals.
Advances in Mathematics,
Vol. 247,
Issue. ,
p.
309.
Duane, A.
Garsia, A. M.
and
Zabrocki, M.
2013.
A new “dinv” arising from the two part case of the shuffle conjecture.
Journal of Algebraic Combinatorics,
Vol. 37,
Issue. 4,
p.
683.
Garsia, Adriano M.
Xin, Gouce
and
Zabrocki, Mike
2014.
Symmetry: Representation Theory and Its Applications.
Vol. 257,
Issue. ,
p.
227.
Berg, Chris
Bergeron, Nantel
Saliola, Franco
Serrano, Luis
and
Zabrocki, Mike
2014.
A Lift of the Schur and Hall–Littlewood Bases to Non-commutative Symmetric Functions.
Canadian Journal of Mathematics,
Vol. 66,
Issue. 3,
p.
525.
Loehr, Nicholas A.
and
Niese, Elizabeth
2014.
New combinatorial formulations of the shuffle conjecture.
Advances in Applied Mathematics,
Vol. 55,
Issue. ,
p.
22.
Garsia, Adriano M.
Xin, Guoce
and
Zabrocki, Mike
2014.
A three shuffle case of the compositional parking function conjecture.
Journal of Combinatorial Theory, Series A,
Vol. 123,
Issue. 1,
p.
202.
Hicks, Angela
2014.
A Parking Function Bijection supporting the Haglund–Morse–Zabrocki Conjectures.
International Mathematics Research Notices,
Vol. 2014,
Issue. 7,
p.
1853.
Aval, J.-C.
Bergeron, F.
and
Garsia, A.
2015.
Combinatorics of labelled parallelogram polyominoes.
Journal of Combinatorial Theory, Series A,
Vol. 132,
Issue. ,
p.
32.
Bergeron, Francois
Garsia, Adriano
Leven, Emily Sergel
and
Xin, Guoce
2016.
Compositional (km,kn)-Shuffle Conjectures.
International Mathematics Research Notices,
Vol. 2016,
Issue. 14,
p.
4229.
Haglund, Jim
2016.
Recent Trends in Combinatorics.
Vol. 159,
Issue. ,
p.
579.
Dalal, Avinash J.
and
Morse, Jennifer
2017.
Quantum and affine Schubert calculus and Macdonald polynomials.
Advances in Mathematics,
Vol. 312,
Issue. ,
p.
425.
Romero, Marino
2017.
The Delta Conjecture at 𝑞=1.
Transactions of the American Mathematical Society,
Vol. 369,
Issue. 10,
p.
7509.
Garsia, Adriano
Sergel Leven, Emily
Wallach, Nolan
and
Xin, Guoce
2017.
A new plethystic symmetric function operator and the rational compositional shuffle conjecture at t= 1/q.
Journal of Combinatorial Theory, Series A,
Vol. 145,
Issue. ,
p.
57.
Carlsson, Erik
and
Mellit, Anton
2017.
A proof of the shuffle conjecture.
Journal of the American Mathematical Society,
Vol. 31,
Issue. 3,
p.
661.
Sergel, Emily
2017.
A proof of the Square Paths Conjecture.
Journal of Combinatorial Theory, Series A,
Vol. 152,
Issue. ,
p.
363.
Alexandersson, Per
and
Panova, Greta
2018.
LLT polynomials, chromatic quasisymmetric functions and graphs with cycles.
Discrete Mathematics,
Vol. 341,
Issue. 12,
p.
3453.
Loehr, Nicholas A.
and
Warrington, Gregory S.
2019.
Quasisymmetric and Schur expansions of cycle index polynomials.
Discrete Mathematics,
Vol. 342,
Issue. 1,
p.
113.
D’Adderio, Michele
Iraci, Alessandro
and
Vanden Wyngaerd, Anna
2019.
The Schröder case of the generalized Delta conjecture.
European Journal of Combinatorics,
Vol. 81,
Issue. ,
p.
58.
van Willigenburg, Stephanie
2019.
The shuffle conjecture.
Bulletin of the American Mathematical Society,
Vol. 57,
Issue. 1,
p.
77.
Hicks, Angela
2019.
Recent Trends in Algebraic Combinatorics.
Vol. 16,
Issue. ,
p.
159.
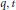 $q,\,t$ -enumeration of Dyck paths that are forced to touch the main diagonal at specific points and forbidden to touch elsewhere and conjecture that it describes the action of the Macdonald theory
$q,\,t$ -enumeration of Dyck paths that are forced to touch the main diagonal at specific points and forbidden to touch elsewhere and conjecture that it describes the action of the Macdonald theory 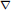 $\nabla $ operator applied to a Hall–Littlewood polynomial. Our conjecture refines several earlier conjectures concerning the space of diagonal harmonics including the “shuffle conjecture” (Duke J. Math. 126 (2005), pp. 195 − 232) for
$\nabla $ operator applied to a Hall–Littlewood polynomial. Our conjecture refines several earlier conjectures concerning the space of diagonal harmonics including the “shuffle conjecture” (Duke J. Math. 126 (2005), pp. 195 − 232) for 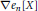 $\nabla {{e}_{n}}\left[ X \right]$ . We bring to light that certain generalized Hall–Littlewood polynomials indexed by compositions are the building blocks for the algebraic combinatorial theory of
$\nabla {{e}_{n}}\left[ X \right]$ . We bring to light that certain generalized Hall–Littlewood polynomials indexed by compositions are the building blocks for the algebraic combinatorial theory of 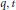 $q,\,t$ -Catalan sequences, and we prove a number of identities involving these functions.
$q,\,t$ -Catalan sequences, and we prove a number of identities involving these functions.
