Hostname: page-component-76c49bb84f-t7r7g Total loading time: 0 Render date: 2025-07-12T22:10:50.403Z Has data issue: false hasContentIssue false
  • English
  • Français

A criterion for the simple normality of fractional powers of two via the Riemann zeta function

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  29 May 2025

Yuya Kanado  and
Kota Saito
Yuya Kanado*
Affiliation:
Graduate School of Mathematics, https://ror.org/04chrp450Nagoya University, Chikusa-ku, Nagoya 464-8601, Japan
Kota Saito
Affiliation:
College of Science & Technology, https://ror.org/05jk51a88Nihon University, Chiyoda-ku, Tokyo 102-0074, Japan saito.kota@nihon-u.ac.jp
*
e-mail: kanadoyuya@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A real number is simply normal to base b if its base-b expansion has each digit appearing with average frequency tending to 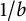$1/b$. In this article, we discover a relation between the frequency at which the digit 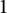$1$ appears in the binary expansion of 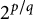$2^{p/q}$ and a mean value of the Riemann zeta function on vertical arithmetic progressions. In particular, we show that

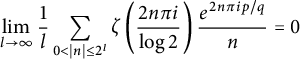$$\begin{align*}\lim_{l\to \infty} \frac{1}{l}\sum_{0<|n|\leq 2^l } \zeta\left(\frac{2 n\pi i}{\log 2}\right) \frac{e^{2n\pi i p/q} }{n} =0 \end{align*}$$
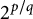if and only if $2^{p/q}$ is simply normal to base 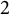$2$.

Keywords

Simple normalityRiemann zeta functionPerron’s formulaexponential integralRidout’s theorem

MSC classification

Primary: 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc. 11M06: $zeta (s)$ and $L(s, chi)$

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 24
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was financially supported by JST SPRING, Grant Number JPMJSP2125. The second author was financially supported by JSPS KAKENHI Grant Number JP22J00025 and JP22KJ0375.

References

Borel, É. M., Les probabilités dénombrables et leurs applications arithmétiques . Rend. del Circ. Mat. di Palermo 27(1909), 247–271.Google Scholar
Good, A., Diskrete Mittel für einige Zetafunktionen . J. Reine Angew. Math. 303(1978), no. 304, 51–73. https://doi.org/10.1515/crll.1978.303-304.51.Google Scholar
Ivić, A., The Riemann zeta-function: Theory and applications. Dover Publications, Inc., Mineola, NY, 2003. xxii+517 pp.Google Scholar
Kobayashi, H., Mean-square values of the Riemann zeta function on arithmetic progressions . Monatsh. Math. 205(2024), no. 4, 787–803.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory I: Classical theory. Cambridge University Press, Cambridge, 2007.Google Scholar
Özbek, S. S. and Steuding, J., The values of the Riemann zeta-function on arithmetic progressions . In: A. Dubickas, A. Laurinčikas, E. Manstavičius and G. Stepanauskas (eds.), Analytic and probabilistic methods in number theory, Vilnius Universiteto Leidykla, Vilnius, 2017, pp. 149–164.Google Scholar
Özbek, S. S. and Steuding, J., The values of the Riemann zeta-function on generalized arithmetic progressions . Arch. Math. (Basel) 112(2019), no. 1, 53–59. https://doi.org/10.1007/s00013-018-1254-1.Google Scholar
Ridout, D., Rational approximations to algebraic numbers . Mathematika 4(1957), 125–131. https://doi.org/10.1112/S0025579300001182.Google Scholar
Steuding, J. and Wegert, E., The Riemann zeta function on arithmetic progressions . Exp. Math. 21(2012), no. 3, 235–240. https://doi.org/10.1080/10586458.2012.651410.Google Scholar
Titchmarsh, E. C., The theory of the Riemann zeta-function. Oxford Science Publication, New York, 1986.Google Scholar