Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-01T19:57:55.138Z Has data issue: false hasContentIssue false
  • English
  • Français

Cubic Twin Prime Polynomials are Counted by a Modular Form

Part of: Finite fields and commutative rings (number-theoretic aspects) Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 January 2019

Lior Bary-Soroker  and
Jakob Stix
Lior Bary-Soroker
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Ramat Aviv, 6997801 Tel Aviv, Israel Email: barylior@post.tau.ac.il
Jakob Stix
Affiliation:
Institut für Mathematik, Goethe–Universität Frankfurt, Robert-Mayer-Straße 6–8, 60325 Frankfurt am Main, Germany Email: stix@math.uni-frankfurt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We present the geometry behind counting twin prime polynomials in 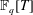$\mathbb{F}_{q}[T]$ in general. We compute cohomology and explicitly count points by means of a twisted Lefschetz trace formula applied to these parametrizing varieties for cubic twin prime polynomials. The elliptic curve 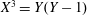$X^{3}=Y(Y-1)$ occurs in the geometry, and thus counting cubic twin prime polynomials involves the associated modular form. In theory, this approach can be extended to higher degree twin primes, but the computations become harder.

The formula we get in degree 3 is compatible with the Hardy–Littlewood heuristic on average, agrees with the prediction for 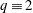$q\equiv 2$ (mod 3), but shows anomalies for 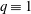$q\equiv 1$ (mod 3).

Keywords

twin primesfinite fieldpolynomial

MSC classification

Primary: 11T55: Arithmetic theory of polynomial rings over finite fields
Secondary: 11G25: Varieties over finite and local fields
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1323 - 1350
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors acknowledge support provided by DAAD-Programm 57271540 Strategische Partnerschaften (supported by BMBF). The first author was partially supported by a grant from the Israel Science Foundation.

References

Andrade, J. C., Bary-Soroker, L., and Rudnick, Z., Shifted convolution and the Titchmarsh divisor problem over F q[t] . Philos. Trans. Roy. Soc. A 373(2015), no. 2040, 20140308. 18 pp. https://doi.org/10.1098/rsta.2014.0308.Google Scholar
Bank, E. and Bary-Soroker, L., Prime polynomial values of linear functions in short intervals . J. Number Theory 151(2015), 263–275. https://doi.org/10.1016/j.jnt.2014.12.016.Google Scholar
Bary-Soroker, L., Hardy–Littlewood tuple conjecture over large finite fields . Int. Math. Res. Not. 2014 no. 2, 568–575. https://doi.org/10.1093/imrn/rns249.Google Scholar
Bary-Soroker, L. and Fehm, A., Correlations of sums of two squares and other arithmetic functions in function fields. 2017. arxiv:1701.04092.Google Scholar
Bender, A. O. and Pollack, P., On quantitative analogues of the Goldbach and twin prime conjectures over F q[t]. 2009. arxiv:0912.1702.Google Scholar
Brun, V., La série 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + 1/41 + 1/43 + 1/59 + 1/61 + ⋯, où les dénominateurs sont nombres premiers jumeaux est convergente ou finie. Bulletin des Sciences Mathématiques, 43(1919), 100–104, 124–128.Google Scholar
Carmon, D., The autocorrelation of the Möbius function and Chowla’s conjecture for the rational function field in characteristic 2 . Philos. Trans. Roy. Soc. A 373(2015), 20140315. 14 pp. https://doi.org/10.1098/rsta.2014.0311.Google Scholar
Castillo, A., Hall, Ch., Lemke Oliver, R. J., Pollack, P., and Thompson, L., Bounded gaps between primes in number fields and function fields . Proc. Amer. Math. Soc. 143(2015), no. 7, 2841–2856. https://doi.org/10.1090/S0002-9939-2015-12554-3.Google Scholar
Chen, J.-R., On the representation of a large even integer as the sum of a prime and the product of at most two primes . Kexue Tongbao 11(1966), no. 9, 385–386.Google Scholar
Deuring, M., Die Zetafunktion einer algebraischen Kurve vom Geschlechte Eins I-III. Nachr. Akad. Wiss. Göttingen, Math.-Phys. Kl. Math.-Phys.-Chem. 1953(1953), 85–94, 1955(1955), 13–42, 1956 (1956), 37–76.Google Scholar
Entin, A., On the Bateman-Horn conjecture for polynomials over large finite fields . Compos. Math. 152(2016), no. 12, 2525–2544. https://doi.org/10.1112/S0010437X16007570.Google Scholar
Freitag, E. and Kiehl, R., Étale cohomology and the Weil conjecture. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3, Springer-Verlag, Berlin, 1988. https://doi.org/10.1007/978-3-662-02541-3.Google Scholar
Granville, A., Primes in intervals of bounded length . Bulletin of the AMS 52(2015), 171–222. https://doi.org/10.1090/S0273-0979-2015-01480-1.Google Scholar
Green, B. and Tao, T., The primes contain arbitrarily long arithmetic progressions . Ann. of Math. 167(2008), no. 2, 481–547. https://doi.org/10.4007/annals.2008.167.481.Google Scholar
Green, B., Tao, T., and Ziegler, T., An inverse theorem for the Gowers U s+1[N]-norm . Ann. of Math. 176(2012), no. 2, 1231–1372. https://doi.org/10.4007/annals.2012.176.2.11.Google Scholar
Hall, C., L-functions of twisted Legendre curves . J. Number Theory 119(2006), no. 1, 128–147. https://doi.org/10.1016/j.jnt.2005.10.004.Google Scholar
Hardy, G. H. and Littlewood, J. E., Some problems of ‘Partitio numerorum’; III: On the expression of a number as a sum of primes . Acta Math. 44(1923), no. 1, 1–70. https://doi.org/10.1007/BF02403921.Google Scholar
Hast, D. and Matei, V., Higher moments of arithmetic functions in short intervals: a geometric perspective. International Mathematics Research Notices, rnx310. https://doi.org/10.1093/imrn/rnx310.Google Scholar
Hecke, E., Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen. Math. Z. 1(1918), no. 4, 357–376; Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen, Math. Z. 6(1920), no. 1–2, 11–51. https://doi.org/10.1007/BF01465095.Google Scholar
Katz, N. M., On a question of Keating and Rudnick about primitive Dirichlet characters with squarefree conductor . Int. Math. Res. Not. IMRN 2013 no. 14, 3221–3249. https://doi.org/10.1093/imrn/rns143.Google Scholar
Katz, N. M., Witt vectors and a question of Keating and Rudnick . Int. Math. Res. Not. IMRN 2013 no. 16, 3613–3638. https://doi.org/10.1093/imrn/rns144.Google Scholar
Keating, J. P. and Rudnick, Z., The variance of the number of prime polynomials in short intervals and in residue classes . Int. Math. Res. Not. IMRN 2014 no. 1, 259–288. https://doi.org/10.1093/imrn/rns220.Google Scholar
Keating, J. P. and Roditty-Gershon, E., Arithmetic correlations over large finite fields. Int. Math. Res. Not. IMRN 2016, 860–874. https://doi.org/10.1093/imrn/rnv157.Google Scholar
The LMFDB Collaboration, The L-functions and modular forms database. 2017. http://www.lmfdb.org [Online; accessed 28 September 2017].Google Scholar
Maynard, J., Small gaps between primes . Ann. of Math. (2) 181(2015), 383–413. https://doi.org/10.4007/annals.2015.181.1.7.Google Scholar
Pollack, P., An explicit approach to Hypothesis H for polynomials over finite fields. In: Anatomy of integers, CRM Proceedings and Lecture Notes, 46, American Mathematical Society, 2008, pp. 47–64.Google Scholar
Polymath, D. H. J., New equidistribution estimates of Zhang type . Algebra & Number Theory 8(2014), no. 9, 2067–2199. https://doi.org/10.2140/ant.2014.8.2067.Google Scholar
Serre, J.-P., A Course in arithmetic. Graduate Texts in Mathematics, 7, Springer-Verlag, New York-Heidelberg, 1973.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves. Second ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009. https://doi.org/10.1007/978-0-387-09494-6.Google Scholar
Skorobogatov, A., Torsors and rational points. Cambridge Tracts in Mathematics, 144, Cambridge University Press, Cambridge, 2001. https://doi.org/10.1017/CBO9780511549588.Google Scholar
Sutherland, A. V., Sato-Tate distributions. 2017. arxiv:1604.01256v4.Google Scholar
Zhang, Y., Bounded gaps between primes . Ann. of Math. 179(2014), no. 3, 1121–1174. https://doi.org/10.4007/annals.2014.179.3.7.Google Scholar