Published online by Cambridge University Press: 20 November 2018
Let 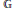 $\mathbb{G}$ be a step-two nilpotent group of
$\mathbb{G}$ be a step-two nilpotent group of 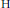 $\text{H}$-type with Lie algebra
$\text{H}$-type with Lie algebra 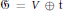 $\mathfrak{G}\,=\,V\,\oplus \,\text{t}$. We define a class of vector fields
$\mathfrak{G}\,=\,V\,\oplus \,\text{t}$. We define a class of vector fields 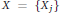 $X\,=\,\left\{ {{X}_{j}} \right\}$ on
$X\,=\,\left\{ {{X}_{j}} \right\}$ on 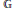 $\mathbb{G}$ depending on a real parameter
$\mathbb{G}$ depending on a real parameter 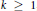 $k\,\ge \,1$, and we consider the corresponding
$k\,\ge \,1$, and we consider the corresponding 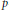 $p$-Laplacian operator
$p$-Laplacian operator 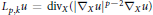 ${{L}_{p,\,k}}u\,=\,di{{v}_{X}}\left( {{\left| {{\nabla }_{X}}u \right|}^{p-2}}{{\nabla }_{X}}u \right)$. For
${{L}_{p,\,k}}u\,=\,di{{v}_{X}}\left( {{\left| {{\nabla }_{X}}u \right|}^{p-2}}{{\nabla }_{X}}u \right)$. For 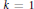 $k\,=\,1$ the vector fields
$k\,=\,1$ the vector fields 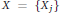 $X\,=\,\left\{ {{X}_{j}} \right\}$ are the left invariant vector fields corresponding to an orthonormal basis of
$X\,=\,\left\{ {{X}_{j}} \right\}$ are the left invariant vector fields corresponding to an orthonormal basis of  $V$; for
$V$; for 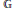 $\mathbb{G}$ being the Heisenberg group the vector fields are the Greiner fields. In this paper we obtain the fundamental solution for the operator
$\mathbb{G}$ being the Heisenberg group the vector fields are the Greiner fields. In this paper we obtain the fundamental solution for the operator 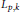 ${{L}_{p,\,k}}$ and as an application, we get a Hardy type inequality associated with
${{L}_{p,\,k}}$ and as an application, we get a Hardy type inequality associated with 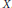 $X$.
$X$.
The first author’s research was supported by NNSF of China (10871180), NSF of Zhejiang province (Y6090359, Y6090383) and Department of Education, Zhejiang (Z200803357) The second author was supported by the Swedish Research Council and a STINT Institutional Grant.