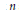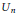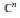Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kodama, Akio
and
Shimizu, Satoru
2003.
A CHARACTERIZATION OF Ck×(C*)ℓFROM THE VIEWPOINT OF BIHOLOMORPHIC AUTOMORPHISM GROUPS.
Journal of the Korean Mathematical Society,
Vol. 40,
Issue. 3,
p.
563.
Isaev, A. V.
2004.
Characterization of the unit ball in C
n
among complex manifolds of dimensionn
.
The Journal of Geometric Analysis,
Vol. 14,
Issue. 4,
p.
697.
Isaev, A. V.
2005.
Hyperbolic manifolds of dimensionn with automorphism group of dimensionn 2 − 1.
Journal of Geometric Analysis,
Vol. 15,
Issue. 2,
p.
239.
Isaev, A. V.
2005.
On hyperbolicn-dimensional manifolds with automorphism group of dimensionn2.
Complex Variables, Theory and Application: An International Journal,
Vol. 50,
Issue. 5,
p.
345.
KODAMA, Akio
and
SHIMIZU, Satoru
2006.
A group-theoretic characterization of the space obtained by omitting the coordinate hyperplanes from the complex Euclidean space, II.
Journal of the Mathematical Society of Japan,
Vol. 58,
Issue. 3,
Isaev, A. V.
2007.
Proper actions of high-dimensional groups on complex manifolds.
Journal of Geometric Analysis,
Vol. 17,
Issue. 4,
p.
649.
Kodama, Akio
and
Shimizu, Satoru
2008.
An intrinsic characterization of the unit polydisc.
Michigan Mathematical Journal,
Vol. 56,
Issue. 1,
Isaev, Alexander V
2008.
Hyperbolic 2–dimensional manifolds with 3–dimensional automorphism group.
Geometry & Topology,
Vol. 12,
Issue. 2,
p.
643.
Isaev, A. V.
2008.
A Remark on a Theorem by Kodama and Shimizu.
Journal of Geometric Analysis,
Vol. 18,
Issue. 3,
p.
795.
Isaev, A.V.
2008.
On proper actions of Lie groups of dimension n2+1 on n-dimensional complex manifolds.
Journal of Mathematical Analysis and Applications,
Vol. 342,
Issue. 2,
p.
1160.
Isaev, A. V.
and
Kruzhilin, N. G.
2009.
Proper actions of lie groups of dimension n
2 + 1 on n-dimensional complex manifolds.
Israel Journal of Mathematics,
Vol. 172,
Issue. 1,
p.
193.
Andrist, Rafael
2010.
Stein spaces characterized by their endomorphisms.
Transactions of the American Mathematical Society,
Vol. 363,
Issue. 5,
p.
2341.
Huckleberry, Alan
and
Isaev, Alexander
2010.
Classical Symmetries of Complex Manifolds.
Journal of Geometric Analysis,
Vol. 20,
Issue. 1,
p.
132.
Byun, Jisoo
Kodama, Akio
and
Shimizu, Satoru
2010.
A group-theoretic characterization of the direct product of a ball and punctured planes.
Tohoku Mathematical Journal,
Vol. 62,
Issue. 4,
Geatti, Laura
Iannuzzi, Andrea
and
Loeb, Jean-Jacques
2011.
A characterization of bounded symmetric domains of type IV.
Manuscripta Mathematica,
Vol. 135,
Issue. 1-2,
p.
183.
Krantz, Steven G.
2013.
The automorphism groups of domains in complex space: a survey.
Quaestiones Mathematicae,
Vol. 36,
Issue. 2,
p.
225.
Isaev, A. V.
2015.
Proper actions of high-dimensional groups on complex manifolds.
Bulletin of Mathematical Sciences,
Vol. 5,
Issue. 2,
p.
251.
Isaev, Alexander
2017.
Effective Transitive Actions of the Unitary Group on Quotients of Hopf Manifolds.
The Journal of Geometric Analysis,
Vol. 27,
Issue. 3,
p.
1914.
Kodama, Akio
2019.
A group-theoretic characterization of the Fock-Bargmann-Hartogs domains.
Tohoku Mathematical Journal,
Vol. 71,
Issue. 4,
Krantz, Steven G.
2021.
Automorphism group actions in complex analysis.
Expositiones Mathematicae,
Vol. 39,
Issue. 1,
p.
78.