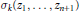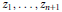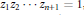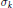Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lubotzky, Alexander
Samuels, Beth
and
Vishne, Uzi
2005.
Ramanujan complexes of typeà d.
Israel Journal of Mathematics,
Vol. 149,
Issue. 1,
p.
267.
Golubev, Konstantin
and
Parzanchevski, Ori
2019.
Spectrum and combinatorics of two-dimensional Ramanujan complexes.
Israel Journal of Mathematics,
Vol. 230,
Issue. 2,
p.
583.
Sendov, Hristo
2021.
Refinements of the Gauss-Lucas theorem using rational lemniscates and polar convexity.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 12,
p.
5179.
Sendov, Hristo
and
Xiao, Junquan
2024.
On the Geometry of Multi-affine Polynomials: Invariant Circles and Circular Solutions.
Computational Methods and Function Theory,