Article contents
Flow Polytopes and the Space of Diagonal Harmonics
Published online by Cambridge University Press: 07 January 2019
Abstract
A result of Haglund implies that the 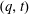 $(q,t)$-bigraded Hilbert series of the space of diagonal harmonics is a
$(q,t)$-bigraded Hilbert series of the space of diagonal harmonics is a 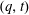 $(q,t)$-Ehrhart function of the flow polytope of a complete graph with netflow vector
$(q,t)$-Ehrhart function of the flow polytope of a complete graph with netflow vector 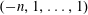 $(-n,1,\ldots ,1)$. We study the
$(-n,1,\ldots ,1)$. We study the 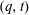 $(q,t)$-Ehrhart functions of flow polytopes of threshold graphs with arbitrary netflow vectors. Our results generalize previously known specializations of the mentioned bigraded Hilbert series at
$(q,t)$-Ehrhart functions of flow polytopes of threshold graphs with arbitrary netflow vectors. Our results generalize previously known specializations of the mentioned bigraded Hilbert series at  $t=1$,
$t=1$, 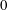 $0$, and
$0$, and 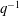 $q^{-1}$. As a corollary to our results, we obtain a proof of a conjecture of Armstrong, Garsia, Haglund, Rhoades, and Sagan about the
$q^{-1}$. As a corollary to our results, we obtain a proof of a conjecture of Armstrong, Garsia, Haglund, Rhoades, and Sagan about the 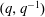 $(q,q^{-1})$-Ehrhart function of the flow polytope of a complete graph with an arbitrary netflow vector.
$(q,q^{-1})$-Ehrhart function of the flow polytope of a complete graph with an arbitrary netflow vector.
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
Mészáros was partially supported by a National Science Foundation Grant (DMS 1501059). Morales was partially supported by an AMS-Simons travel grant.
References
- 3
- Cited by

