Hostname: page-component-5b777bbd6c-7sgmh Total loading time: 0 Render date: 2025-06-24T12:11:16.802Z Has data issue: false hasContentIssue false
  • English
  • Français

A Galois Correspondence for Reduced Crossed Products of Simple 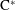$\text{C}^{\ast }$-algebras by Discrete Groups

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  07 January 2019

Jan Cameron  and
Roger R. Smith
Jan Cameron
Affiliation:
Department of Mathematics, Vassar College, Poughkeepsie, NY 12604, USA Email: jacameron@vassar.edu
Roger R. Smith
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843-3368, USA Email: rsmith@math.tamu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a discrete group 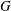$G$ act on a unital simple 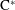$\text{C}^{\ast }$-algebra 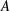$A$ by outer automorphisms. We establish a Galois correspondence 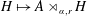$H\mapsto A\rtimes _{\unicode[STIX]{x1D6FC},r}H$ between subgroups of 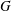$G$ and 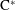$\text{C}^{\ast }$-algebras 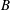$B$ satisfying 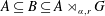$A\subseteq B\subseteq A\rtimes _{\unicode[STIX]{x1D6FC},r}G$, where 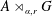$A\rtimes _{\unicode[STIX]{x1D6FC},r}G$ denotes the reduced crossed product. For a twisted dynamical system 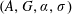$(A,G,\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D70E})$, we also prove the corresponding result for the reduced twisted crossed product 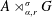$A\rtimes _{\unicode[STIX]{x1D6FC},r}^{\unicode[STIX]{x1D70E}}G$.

Keywords

C∗ -algebragroupcrossed productbimodulereducedtwisted

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46L40: Automorphisms
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 1103 - 1125
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author J. C. was partially supported by Simons Collaboration Grant for Mathematicians #319001. Author R. S. was partially supported by Simons Collaboration Grant for Mathematicians #522375.

References

Bédos, E., Discrete groups and simple C∗-algebras . Math. Proc. Cam. Phil. Soc. 109(1991), 521–537. https://doi.org/10.1017/S0305004100069966.Google Scholar
Bonsall, F. F. and Duncan, J., Complete normed algebras . Ergebnisse der Mathematik und ihrer Grenzgebiete, 80, Springer-Verlag, New York-Heidelberg, 1973.Google Scholar
Bryder, R. S. and Kennedy, M., Reduced twisted crossed products over C∗-simple groups . Int. Math. Res. Not. IMRN 2018 no. 6, 1638–1655. https://doi.org/10.1093/imrn/rnw296.Google Scholar
Bures, D., Abelian subalgebras of von Neumann algebras . Memoirs of the American Mathematical Society, 110, American Mathematical Society, Providence, RI, 1971.Google Scholar
Cameron, J. M., Hochschild cohomology of II 1 factors with Cartan maximal abelian subalgebras . Proc. Edinb. Math. Soc. 52(2009), no. 2, 287–295. https://doi.org/10.1017/S0013091507000053.Google Scholar
Cameron, J., Pitts, D. R., and Zarikian, V., Bimodules over Cartan MASAs in von Neumann algebras, norming algebras, and Mercer’s theorem . New York J. Math. 19(2013), 455–486.Google Scholar
Cameron, J. and Smith, R. R., Bimodules in crossed products of von Neumann algebras . Adv. Math. 274(2015), 539–561. https://doi.org/10.1016/j.aim.2014.12.038.Google Scholar
Cameron, J. and Smith, R. R., Intermediate subalgebras and bimodules for general crossed products of von Neumann algebras . Internat. J. Math. 27(2016), no. 11, 1650091. https://doi.org/10.1142/S0129167X16500919.Google Scholar
Choda, H., A Galois correspondence in a von Neumann algebra . Tôhoku Math. J. 30(1978), 491–504. https://doi.org/10.2748/tmj/1178229909.Google Scholar
Choda, H., A correspondence between subgroups and subalgebras in a discrete C∗-crossed product . Math. Japon. 24(1979/80), 225–229.Google Scholar
Choi, M. D., Completely positive linear maps on complex matrices . Linear Algebra and Appl. 10(1975), 285–290. https://doi.org/10.1016/0024-3795(75)90075-0.Google Scholar
Christensen, E. and Sinclair, A. M., Module mappings into von Neumann algebras and injectivity . Proc. London Math. Soc. 71(1995), 618–640. https://doi.org/10.1112/plms/s3-71.3.618.Google Scholar
Elliott, G. A., Some simple C∗-algebras constructed as crossed products with discrete outer automorphism groups . Publ. Res. Inst. Math. Sci. 16(1980), 299–311. https://doi.org/10.2977/prims/1195187509.Google Scholar
Glimm, J., A Stone-Weierstrass theorem for C∗-algebras . Ann. of Math. 72(1960), 216–244. https://doi.org/10.2307/1970133.Google Scholar
Haagerup, U. and Kraus, J., Approximation properties for group C∗-algebras and group von Neumann algebras . Trans. Amer. Math. Soc. 344(1994), 667–699. https://doi.org/10.2307/2154501.Google Scholar
Haagerup, U. and Zsidó, L., Sur la propriété de Dixmier pour les C∗-algèbres . C. R. Acad. Sci. Paris Sér. I Math. 298(1984), 173–176.Google Scholar
Halpern, H., Essential central spectrum and range for elements of a von Neumann algebra . Pacific J. Math. 43(1972), 349–380. https://doi.org/10.2140/pjm.1972.43.349.Google Scholar
Izumi, M., Inclusions of simple C∗-algebras . J. Reine Angew. Math. 547(2002), 97–138. https://doi.org/10.1515/crll.2002.055.Google Scholar
Izumi, M., Longo, R., and Popa, S., A Galois correspondence for compact groups of automorphisms of von Neumann algebras with a generalization to Kac algebras . J. Funct. Anal. 155(1998), 25–63. https://doi.org/10.1006/jfan.1997.3228.Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the theory of operator algebras. Vol. II. Advanced theory . Pure and Applied Mathematics, 100, Academic Press, Inc., Orlando, FL, 1986. https://doi.org/10.1016/S0079-8169(08)60611-X.Google Scholar
Kishimoto, A., Simple crossed products of C∗-algebras by locally compact abelian groups . Yokohama Math. J. 28(1980), 69–85.Google Scholar
Kishimoto, A., Outer automorphisms and reduced crossed products of simple C∗-algebras . Comm. Math. Phys. 81(1981), 429–435. https://doi.org/10.1007/BF01209077.Google Scholar
Landstad, M. B., Olesen, D., and Pedersen, G. K., Towards a Galois theory for crossed products of C∗-algebras . Math. Scand. 43(1978), 311–321. https://doi.org/10.7146/math.scand.a-11783.Google Scholar
Mercer, R., Bimodules over Cartan subalgebras. Proceedings of the Seventh Great Plains Operator Theory Seminar (Lawrence, KS, 1987). Rocky Mountain J. Math. 20 (1990), 487–502. https://doi.org/10.1216/rmjm/1181073123.Google Scholar
Mercer, R., Isometric isomorphisms of Cartan bimodule algebras . J. Funct. Anal. 101(1991), 10–24. https://doi.org/10.1016/0022-1236(91)90144-T.Google Scholar
Murray, F. J. and von Neumann, J., On rings of operators . Ann. Math. 37(1936), 116–229. https://doi.org/10.2307/1968693.Google Scholar
Olesen, D., Inner ∗-automorphisms of simple C∗-algebras . Comm. Math. Phys. 44(1975), 175–190. https://doi.org/10.1007/BF01608830.Google Scholar
Packer, J. A. and Raeburn, I., Twisted crossed products of C∗-algebras . Math. Proc. Cam. Phil. Soc. 106(1989), 293–311. https://doi.org/10.1017/S0305004100078129.Google Scholar
Phillips, J., Outer automorphisms of separable C∗-algebras . J. Funct. Anal 70(1987), 111–116. https://doi.org/10.1016/0022-1236(87)90125-X.Google Scholar
Pop, F., Sinclair, A. M., and Smith, R. R., Norming C∗-algebras by C∗-subalgebras . J. Funct. Anal. 175(2000), 168–196. https://doi.org/10.1006/jfan.2000.3601.Google Scholar
Quigg, J. C., Duality for reduced twisted crossed products of C∗-algebras . Indiana Univ. Math. J. 35(1986), 549–571. https://doi.org/10.1512/iumj.1986.35.35029.Google Scholar
Sakai, S., Derivations of simple C∗-algebras . J. Funct. Anal. 2(1968), 202–206. https://doi.org/10.1016/0022-1236(68)90017-7.Google Scholar
Sinclair, A. M. and Smith, R. R., Finite von Neumann algebras and masas . London Math. Soc. Lecture Note Series, 351, Cambridge Univ. Press, Cambridge, 2008. https://doi.org/10.1017/CBO9780511666230.Google Scholar
Strǎtilǎ, S., Central spectral theory in W∗-algebras, and applications . (Romanian) Stud. Cerc. Mat. 25(1973), 1167–1259.Google Scholar
Strǎtilǎ, S. and Zsidó, L., An algebraic reduction theory for W∗-algebras. II . Rev. Roumaine Math. Pures Appl. 18(1973), 407–460.Google Scholar
Sutherland, C. E., Cohomology and extensions of von Neumann algebras I . Publ. Res. Inst. Math. Sci. 16(1980), 105–133. https://doi.org/10.2977/prims/1195187501.Google Scholar
Takesaki, M., Theory of operator algebras. I . Springer-Verlag, New York-Heidelberg, 1979.Google Scholar
van Daele, A., Continuous crossed products and type III von Neumann algebras . London Math. Soc. Lecture Note Series, 31, Cambridge Univ. Press, Cambridge, 1978.Google Scholar
Wright, F. B., A reduction for algebras of finite type . Ann. of Math. 60(1954), 560–570. https://doi.org/10.2307/1969851.Google Scholar