Hostname: page-component-76c49bb84f-hwk5l Total loading time: 0 Render date: 2025-07-07T01:18:05.712Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois Representations Over Fields of Moduli and Rational Points on Shimura Curves

Published online by Cambridge University Press:  20 November 2018

Victor Rotger  and
Carlos de Vera-Piquero
Victor Rotger
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, C. Jordi Girona 1-3, 08034 Barcelona, Spain. e-mail: victor.rotger@upc.edu. e-mail: carlos.de.vera@upc.edu
Carlos de Vera-Piquero
Affiliation:
Departament de Matemàtica Aplicada II, Universitat Politècnica de Catalunya, C. Jordi Girona 1-3, 08034 Barcelona, Spain. e-mail: victor.rotger@upc.edu. e-mail: carlos.de.vera@upc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this note is to introduce a method for proving the non-existence of rational points on a coarse moduli space 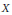$X$ of abelian varieties over a given number field 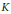$K$ in cases where the moduli problem is not fine and points in 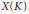$X\left( K \right)$ may not be represented by an abelian variety (with additional structure) admitting a model over the field 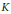$K$. This is typically the case when the abelian varieties that are being classified have even dimension. The main idea, inspired by the work of Ellenberg and Skinner on the modularity of 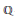$\mathbb{Q}$-curves, is that one may still attach a Galois representation of 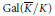$\text{Gal}\left( \bar{K},\,K \right)$ with values in the quotient group 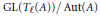$\text{GL}\left( {{T}_{\ell }}\left( A \right) \right)/\,\text{Aut}\left( A \right)$ to a point 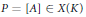$P\,=\,\left[ A \right]\,\in \,X\left( K \right)$ represented by an abelian variety 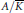$A/\bar{K}$, provided 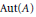$\text{Aut}\left( A \right)$ lies in the centre of $\text{GL}\left( {{T}_{\ell }}\left( A \right) \right)$. We exemplify our method in the cases where 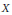$X$ is a Shimura curve over an imaginary quadratic field or an Atkin–Lehner quotient over 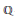$\mathbb{Q}$.

Keywords

11G1814G3514G05Shimura curvesrational pointsGalois representationsHasse principleBrauer–Manin obstruction

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 5 , 01 October 2014 , pp. 1167 - 1200
Copyright
Copyright © Canadian Mathematical Society 2014

References

[BFGR06] Bruin, N., Flynn, V., Gonzàlez, J., and Rotger, V., On finiteness conjectures for endomorphism algebras of abelian surfaces. Math. Proc. Cambridge Philos. Soc. 141(2006), no. 3, 383–408 http://dx.doi.org/10.1017/S0305004106009613.Google Scholar
[Cla03] Clark, P. L., Rational points on Atkin–Lehner quotients of Shimura curves. Thesis (Ph.D.)–Harvard University, ProQuest LLC, Ann Arbor, MI, 2003.Google Scholar
[ES01] Ellenberg, J. S. and Skinner, C., On the modularity of Q-curves. Duke Math. J. 109(2001), no. 1, 97–122 http://dx.doi.org/10.1215/S0012-7094-01-10914-9.Google Scholar
[Gil10] Gillibert, F., Points rationnels sur les quotients d'Atkin–Lehner de courbes de Shimura de discriminant pq. arxiv:1012.3414v1, 2010.Google Scholar
[GR06]González, J. and Rotger, V., Non elliptic Shimura curves of genus one. J. Math. Soc. Japan 58(2006), no. 4, 927–948 http://dx.doi.org/10.2969/jmsj/1179759530.Google Scholar
[Jor81] Jordan, B.W., On the Diophantine arithmetic of Shimura curves. Thesis (Ph.D.)–Harvard University, Proquest LLC, Ann Arbor, MI, 1981.Google Scholar
[Jor86] Jordan, B.W., Points on Shimura curves rational over number fields. J. Reine Angew. Math. 371(1986), 92–114.Google Scholar
[JL85] Jordan, B.W. and Livné, R. A., Local Diophantine properties of Shimura curves. Math. Ann. 270(1985), no. 2, 235–248 http://dx.doi.org/10.1007/BF01456184.Google Scholar
[Me90] Mestre, J.-F., Construction de courbes de genre 2 à partir de leurs modules. In: Effective methods in algebraic geometry (Castiglioncello, 1990), Progr. Math., 94, Birkhäuser Boston, Boston, MA, 1991, pp. 313–334.Google Scholar
[Mil79] Milne, J. S., Points on Shimura varieties mod p. In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence, RI, 1979, pp. 165–184.Google Scholar
[Mil86] Milne, J. S., Abelian varieties. In: Arithmetic geometry (Storrs, Conn, 1984), Springer, New York, 1986, pp. 103–150.Google Scholar
[Mil04] Milne, J. S., Introduction to Shimura varieties. http://www.jmilne.org/math/xnotes.Google Scholar
[Mor81] Morita, Y., Reduction modulo β of Shimura curves. HokkaidoMath. J. 10(1981), no. 2, 209–238.Google Scholar
[Ogg83] Ogg, A. P., Real points on Shimura curves. In: Arithmetic and geometry, Vol. 1, Progr. Math., 35, Birkäuser Boston, Boston, MA, 1983, pp. 277–307.Google Scholar
[Ogg85] Ogg, A. P., Mauvaise réduction des courbes de Shimura. Séminaire de théorie des nombres, Paris 1983–84, Progr. Math., 59, Birkäuser Boston, MA, 1985, pp. 199–217.Google Scholar
[Oht64] Ohta, M., On ladic representations of Galois groups obtained from certain two-dimensional abelian varieties. J. Fac. Sci. Univ. Tokyo IA Math. 21(1974), 299–308.Google Scholar
[PY07] Parent, P. and Yafaev, A., Proving the triviality of rational points on Atkin–Lehner quotients of Shimura curves. Math. Ann. 339(2007), no. 4, 915–935 http://dx.doi.org/10.1007/s00208-007-0136-9.Google Scholar
[Rot03] Rotger, V., Quaternions, polarizations and class numbers. J. Reine Angew. Math. 561(2003), 177–197.Google Scholar
[Rot04] Rotger, V., Modular Shimura varieties and forgetful maps. Trans. Amer. Math. Soc. 356(2004), no. 4, 1535–1550 http://dx.doi.org/10.1090/S0002-9947-03-03408-1.Google Scholar
[Rot08] Rotger, V., Which quaternion algebras act on a modular abelian variety? Math. Res. Lett. 15(2008), no. 2, 251–263.Google Scholar
[RSY05] Rotger, V., Skorobogatov, A., and Yafaev, A., Failure of the Hasse principle for Atkin–Lehner quotients of Shimura curves over Q. Moscow Math. J. 5(2005), no. 2, 463–476, 495.Google Scholar
[Ser72] Serre, J.-P., Propriétés galoisiennes des points d'ordre fini des courbes elliptiques. Invent. Math. 15(1972), no. 4, 259–331 http://dx.doi.org/10.1007/BF01405086.Google Scholar
[ST68] Serre, J.-P. and Tate, J. , Good reduction of abelian varieties. Ann. of Math. 88(1968), 492–517 http://dx.doi.org/10.2307/1970722.Google Scholar
[Shi63] Shimura, G., On analytic families of polarized abelian varieties and automorphic functions. Ann.of Math. 78(1963), 149–192 http://dx.doi.org/10.2307/1970507.Google Scholar
[Shi67] Shimura, G., Construction of class fields and zeta functions of algebraic curves. Ann. of Math. 85(1967), 58–159 http://dx.doi.org/10.2307/1970526.Google Scholar
[Shi75] Shimura, G., On the real points of an arithmetic quotient of a bounded symmetric domain. Math. Ann. 215(1975), 135–164 http://dx.doi.org/10.1007/BF01432692.Google Scholar
[Sko01] Skorobogatov, A., Torsors and rational points. Cambridge Tracts in Mathematics, 144, Cambridge University Press, Cambridge, 2001.Google Scholar
[Sko05] Skorobogatov, A., Shimura coverings of Shimura curves and the Manin obstruction. Math. Res. Lett. 12(2005), no. 5–6, 779–788.Google Scholar
[SY04] Skorobogatov, A. and Yafaev, A., Descent on certain Shimura curves. Israel J. Math. 140(2004).319–332 http://dx.doi.org/10.1007/BF02786638.Google Scholar
[dVP] de Vera-Piquero, C., The Shimura covering of a Shimura curve: automorphisms and étale subcoverings. J. Number Theory 133(2013), no. 10, 3500–3516 http://dx.doi.org/10.1016/j.jnt.2013.04.018.Google Scholar
[Vig80] Vignéras, M. F., Arithmétique des algébres de quaternions. Lecture Notes in Mathematics, 800, Springer, Berlin, 1980.Google Scholar
[Wei56] Weil, A., The field of definition of a variety. Amer. J. Math. 78(1956), 509–524 http://dx.doi.org/10.2307/2372670.Google Scholar