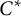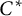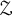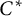1 Introduction
The generator rank of a unital, separable
![]() $C^*\!$
-algebra A is the smallest integer
$C^*\!$
-algebra A is the smallest integer
![]() $n\geq 0$
such that the self-adjoint
$n\geq 0$
such that the self-adjoint
![]() $(n+1)$
-tuples that generate A as a
$(n+1)$
-tuples that generate A as a
![]() $C^*\!$
-algebra are dense in
$C^*\!$
-algebra are dense in
![]() $A^{n+1}_{\mathrm {sa}}$
(see Definition 2.1 for the nonunital and nonseparable case). This invariant was introduced in [Reference Thiel and WinterThi21] to study the generator problem, which asks to determine the minimal number of (self-adjoint) generators for a given
$A^{n+1}_{\mathrm {sa}}$
(see Definition 2.1 for the nonunital and nonseparable case). This invariant was introduced in [Reference Thiel and WinterThi21] to study the generator problem, which asks to determine the minimal number of (self-adjoint) generators for a given
![]() $C^*\!$
-algebra.
$C^*\!$
-algebra.
One difficulty when studying the generator problem is that the minimal number of generators for a
![]() $C^*\!$
-algebra can increase when passing to ideals or inductive limits. The main advantage of the generator rank is that it enjoys nice permanence properties: it does not increase when passing to ideals, quotients, or inductive limits (see Section 2).
$C^*\!$
-algebra can increase when passing to ideals or inductive limits. The main advantage of the generator rank is that it enjoys nice permanence properties: it does not increase when passing to ideals, quotients, or inductive limits (see Section 2).
For example, using these permanence properties, one can easily show that approximately finite-dimensional
![]() $C^*\!$
-algebras (AF-algebras) have generator rank at most one. In particular, every AF-algebra is generated by two self-adjoint elements, which solves the generator problem for this class of algebras (see [Reference Thiel and WinterThi21, Theorem 7.3]).
$C^*\!$
-algebras (AF-algebras) have generator rank at most one. In particular, every AF-algebra is generated by two self-adjoint elements, which solves the generator problem for this class of algebras (see [Reference Thiel and WinterThi21, Theorem 7.3]).
In this paper, we compute the generator rank of subhomogeneous
![]() $C^*\!$
-algebras. Recall that a
$C^*\!$
-algebras. Recall that a
![]() $C^*\!$
-algebra is said to be d-homogeneous (d-subhomogeneous) if each of its irreducible representations has dimension (at most) d. The typical example of a d-homogeneous
$C^*\!$
-algebra is said to be d-homogeneous (d-subhomogeneous) if each of its irreducible representations has dimension (at most) d. The typical example of a d-homogeneous
![]() $C^*\!$
-algebra is
$C^*\!$
-algebra is
![]() $C_0(X,M_d)$
for a locally compact Hausdorff space X. Furthermore, a
$C_0(X,M_d)$
for a locally compact Hausdorff space X. Furthermore, a
![]() $C^*\!$
-algebra is subhomogeneous if and only if it is a sub-
$C^*\!$
-algebra is subhomogeneous if and only if it is a sub-
![]() $C^*\!$
-algebra of
$C^*\!$
-algebra of
![]() $C_0(X,M_d)$
for some X and some d (see, for example, [Reference BlackadarBla06, Proposition IV.1.4.3]).
$C_0(X,M_d)$
for some X and some d (see, for example, [Reference BlackadarBla06, Proposition IV.1.4.3]).
Subhomogeneous
![]() $C^*\!$
-algebras and their inductive limits (called approximately subhomogeneous algebras [ASH-algebras]) play an important role in the structure and classification theory of
$C^*\!$
-algebras and their inductive limits (called approximately subhomogeneous algebras [ASH-algebras]) play an important role in the structure and classification theory of
![]() $C^*\!$
-algebras since the algebras covered by the Elliott program are either purely infinite or approximately subhomogeneous. To be precise, let us say that a
$C^*\!$
-algebras since the algebras covered by the Elliott program are either purely infinite or approximately subhomogeneous. To be precise, let us say that a
![]() $C^*\!$
-algebra is classifiable if it is unital, separable, simple, nuclear, and
$C^*\!$
-algebra is classifiable if it is unital, separable, simple, nuclear, and
![]() $\mathcal {Z}$
-stable (that is, it tensorially absorbs the Jiang–Su algebra
$\mathcal {Z}$
-stable (that is, it tensorially absorbs the Jiang–Su algebra
![]() $\mathcal {Z}$
) and satisfies the Universal Coefficient Theorem (UCT). By the recent breakthrough in the Elliott classification program [Reference Elliott, Gong, Lin and NiuEGLN15, Reference Gong, Lin and NiuGLN20, Reference van MillTWW17], two classifiable
$\mathcal {Z}$
) and satisfies the Universal Coefficient Theorem (UCT). By the recent breakthrough in the Elliott classification program [Reference Elliott, Gong, Lin and NiuEGLN15, Reference Gong, Lin and NiuGLN20, Reference van MillTWW17], two classifiable
![]() $C^*\!$
-algebras are isomorphic if and only if their Elliott invariants (K-theoretic and tracial data) are isomorphic.
$C^*\!$
-algebras are isomorphic if and only if their Elliott invariants (K-theoretic and tracial data) are isomorphic.
Classifiable
![]() $C^*\!$
-algebras come in two flavors: stably finite and purely infinite. Every stably finite, classifiable
$C^*\!$
-algebras come in two flavors: stably finite and purely infinite. Every stably finite, classifiable
![]() $C^*\!$
-algebra is automatically an ASH-algebra. A major application of our results is that every
$C^*\!$
-algebra is automatically an ASH-algebra. A major application of our results is that every
![]() $\mathcal {Z}$
-stable ASH-algebra has generator rank one (see Corollary C). In [Reference ThielThi20], we show that every
$\mathcal {Z}$
-stable ASH-algebra has generator rank one (see Corollary C). In [Reference ThielThi20], we show that every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra of real rank zero has generator rank one. This includes all purely infinite, classifiable
$C^*\!$
-algebra of real rank zero has generator rank one. This includes all purely infinite, classifiable
![]() $C^*\!$
-algebras. It follows that every classifiable
$C^*\!$
-algebras. It follows that every classifiable
![]() $C^*\!$
-algebra has generator rank one and therefore contains a dense
$C^*\!$
-algebra has generator rank one and therefore contains a dense
![]() $G_\delta $
-subset of generators (see Corollary E).
$G_\delta $
-subset of generators (see Corollary E).
One important aspect of the generator problem is to determine if every separable, simple
![]() $C^*\!$
-algebra is generated by a single operator (equivalently, by two self-adjoint elements). While this remains unclear, we can refute the possibility that every separable, simple
$C^*\!$
-algebra is generated by a single operator (equivalently, by two self-adjoint elements). While this remains unclear, we can refute the possibility that every separable, simple
![]() $C^*\!$
-algebra contains a dense set of generators: Villadsen constructed examples of separable, simple, approximately homogeneous
$C^*\!$
-algebra contains a dense set of generators: Villadsen constructed examples of separable, simple, approximately homogeneous
![]() $C^*\!$
-algebras (AH-algebras) of arbitrarily high real rank (see [Reference VilladsenVil99]). Let A be such an AH-algebra with
$C^*\!$
-algebras (AH-algebras) of arbitrarily high real rank (see [Reference VilladsenVil99]). Let A be such an AH-algebra with
![]() $\operatorname {\mathrm {rr}}(A)=\infty $
. By [Reference Thiel and WinterThi21, Proposition 3.10] (see Proposition 2.4), the real rank is dominated by the generator rank, whence
$\operatorname {\mathrm {rr}}(A)=\infty $
. By [Reference Thiel and WinterThi21, Proposition 3.10] (see Proposition 2.4), the real rank is dominated by the generator rank, whence
![]() $\operatorname {\mathrm {gr}}(A)=\infty $
. In particular, for every n, the generating self-adjoint n-tuples (if there are any) are not dense in
$\operatorname {\mathrm {gr}}(A)=\infty $
. In particular, for every n, the generating self-adjoint n-tuples (if there are any) are not dense in
![]() $A^{n}_{\mathrm {sa}}$
.
$A^{n}_{\mathrm {sa}}$
.
In [Reference Tikuisis, White and WinterTW14, Theorem 3.8], the author and Winter showed that every unital, separable,
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra is singly generated. The results of this paper and of [Reference ThielThi20] show that under additional assumptions, a (unital) separable,
$C^*\!$
-algebra is singly generated. The results of this paper and of [Reference ThielThi20] show that under additional assumptions, a (unital) separable,
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra even contains a dense set of generators. This raises the natural question if every
$C^*\!$
-algebra even contains a dense set of generators. This raises the natural question if every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra has generator rank one (see [Reference ThielThi20, Remarks 5.8(2)]).
$C^*\!$
-algebra has generator rank one (see [Reference ThielThi20, Remarks 5.8(2)]).
Given a locally compact Hausdorff space X, the local dimension
![]() $\operatorname {\mathrm {locdim}}(X)$
is defined as the supremum of the covering dimension of all compact subsets, with the convention that
$\operatorname {\mathrm {locdim}}(X)$
is defined as the supremum of the covering dimension of all compact subsets, with the convention that
![]() $\operatorname {\mathrm {locdim}}(\emptyset )=-1$
. For
$\operatorname {\mathrm {locdim}}(\emptyset )=-1$
. For
![]() $\sigma $
-compact (in particular, second countable), locally compact Hausdorff spaces, the local dimension agrees with the usual covering dimension (in general they differ). In Section 4, we compute the generator rank of arbitrary homogeneous
$\sigma $
-compact (in particular, second countable), locally compact Hausdorff spaces, the local dimension agrees with the usual covering dimension (in general they differ). In Section 4, we compute the generator rank of arbitrary homogeneous
![]() $C^*\!$
-algebras.
$C^*\!$
-algebras.
Theorem A (4.17)
Let A be a d-homogeneous
![]() $C^*\!$
-algebra. Set
$C^*\!$
-algebra. Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. If
$X:=\operatorname {\mathrm {Prim}}(A)$
. If
![]() $d=1$
, then
$d=1$
, then
![]() $\operatorname {\mathrm {gr}}(A) = \operatorname {\mathrm {locdim}}(X\times X)$
. If
$\operatorname {\mathrm {gr}}(A) = \operatorname {\mathrm {locdim}}(X\times X)$
. If
![]() $d\geq 2$
, then
$d\geq 2$
, then
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil. \end{align*} $$
In particular,
![]() $\operatorname {\mathrm {gr}}(C(X,M_d)) = \left \lceil \tfrac {\dim (X)+1}{2d-2}\right \rceil $
if X is a compact Hausdorff space and
$\operatorname {\mathrm {gr}}(C(X,M_d)) = \left \lceil \tfrac {\dim (X)+1}{2d-2}\right \rceil $
if X is a compact Hausdorff space and
![]() $d\geq 2$
. To prove Theorem A, we first show a Stone–Weierstraß-type result that characterizes when a tuple generates
$d\geq 2$
. To prove Theorem A, we first show a Stone–Weierstraß-type result that characterizes when a tuple generates
![]() $C(X,M_d)$
: the tuple has to generate
$C(X,M_d)$
: the tuple has to generate
![]() $M_d$
pointwise, and it has to suitably separate the points in X (see Proposition 4.1). This indicates the general strategy to determine when generating n-tuples in
$M_d$
pointwise, and it has to suitably separate the points in X (see Proposition 4.1). This indicates the general strategy to determine when generating n-tuples in
![]() $C(X,M_d)$
are dense: first, we need to characterize when every tuple can be approximated by tuples that generate
$C(X,M_d)$
are dense: first, we need to characterize when every tuple can be approximated by tuples that generate
![]() $M_d$
pointwise, and second, we need to characterize when a pointwise generating tuple can be approximated by tuples that separate the points. To address the first point, we compute the codimension of the manifold of generating n-tuples of self-adjoint d-matrices (see Lemma 4.11). For the second point, we use known results characterizing when continuous maps to a manifold can be approximated by embeddings, in conjunction with a suitable version of the homotopy extension lifting property.
$M_d$
pointwise, and second, we need to characterize when a pointwise generating tuple can be approximated by tuples that separate the points. To address the first point, we compute the codimension of the manifold of generating n-tuples of self-adjoint d-matrices (see Lemma 4.11). For the second point, we use known results characterizing when continuous maps to a manifold can be approximated by embeddings, in conjunction with a suitable version of the homotopy extension lifting property.
In Section 5, we compute the generator rank of d-subhomogeneous
![]() $C^*\!$
-algebras by induction over d. Given a d-subhomogeneous
$C^*\!$
-algebras by induction over d. Given a d-subhomogeneous
![]() $C^*\!$
-algebra A, we consider the ideal
$C^*\!$
-algebra A, we consider the ideal
![]() $I\subseteq A$
corresponding to irreducible representations of dimension d. Then
$I\subseteq A$
corresponding to irreducible representations of dimension d. Then
![]() $A/I$
is
$A/I$
is
![]() $(d-1)$
-subhomogeneous. Using Theorem A and the assumption of the induction, we know the generator rank of I and
$(d-1)$
-subhomogeneous. Using Theorem A and the assumption of the induction, we know the generator rank of I and
![]() $A/I$
. The crucial result to compute the generator rank of the extension is the following proposition, which we also expect to have further applications in the future.
$A/I$
. The crucial result to compute the generator rank of the extension is the following proposition, which we also expect to have further applications in the future.
Proposition B (5.3)
Let A be a separable
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals satisfying
$(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals satisfying
![]() $\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Then,
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Then,
The main result of this paper is the following theorem.
Theorem C (5.5)
Let A be a subhomogeneous
![]() $C^*\!$
-algebra. For each
$C^*\!$
-algebra. For each
![]() $d\geq 1$
, set
$d\geq 1$
, set
![]() $X_d:=\operatorname {\mathrm {Prim}}_d(A)$
, the subset of the primitive ideal space of A corresponding to d-dimensional irreducible representations. Then,
$X_d:=\operatorname {\mathrm {Prim}}_d(A)$
, the subset of the primitive ideal space of A corresponding to d-dimensional irreducible representations. Then,
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \max_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \max_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*} $$
The main application is the following corollary.
Corollary D (5.10)
Let A be a nonzero, separable,
![]() $\mathcal {Z}$
-stable ASH-algebra. Then,
$\mathcal {Z}$
-stable ASH-algebra. Then,
![]() $\operatorname {\mathrm {gr}}(A)=1$
, and so a generic element of A is a generator.
$\operatorname {\mathrm {gr}}(A)=1$
, and so a generic element of A is a generator.
It was shown in [Reference Tikuisis, White and WinterTW14, Theorem 3.8] that every unital, separable,
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra is singly generated. We note that Corollary D does not require unitality. In particular, Corollary D implies that certain
$C^*\!$
-algebra is singly generated. We note that Corollary D does not require unitality. In particular, Corollary D implies that certain
![]() $C^*\!$
-algebras are singly generated that were not considered in [Reference Tikuisis, White and WinterTW14].
$C^*\!$
-algebras are singly generated that were not considered in [Reference Tikuisis, White and WinterTW14].
Together with the main result of [Reference ThielThi20], we obtain the following consequence.
Corollary E [Reference ThielThi20, Corollary 5.7]
Let A be a unital, separable, simple, nuclear,
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra satisfying the UCT. Then, A has generator rank one. In particular, a generic element in A is a generator.
$C^*\!$
-algebra satisfying the UCT. Then, A has generator rank one. In particular, a generic element in A is a generator.
Notation We set
![]() $\mathbb {N}:=\{0,1,2,\ldots \}$
. Given a
$\mathbb {N}:=\{0,1,2,\ldots \}$
. Given a
![]() $C^*\!$
-algebra A, we use
$C^*\!$
-algebra A, we use
![]() $A_{\mathrm {sa}}$
to denote the set of self-adjoint elements in A. We denote by
$A_{\mathrm {sa}}$
to denote the set of self-adjoint elements in A. We denote by
![]() $\widetilde {A}$
the minimal unitization of A. By an ideal in a
$\widetilde {A}$
the minimal unitization of A. By an ideal in a
![]() $C^*\!$
-algebra, we mean a closed, two-sided ideal. We write
$C^*\!$
-algebra, we mean a closed, two-sided ideal. We write
![]() $M_d$
for the
$M_d$
for the
![]() $C^*\!$
-algebra of d-by-d matrices
$C^*\!$
-algebra of d-by-d matrices
![]() $M_d(\mathbb {C})$
.
$M_d(\mathbb {C})$
.
Given
![]() $a,b\in A$
, and
$a,b\in A$
, and
![]() $\varepsilon>0$
, we write
$\varepsilon>0$
, we write
![]() $a=_\varepsilon b$
if
$a=_\varepsilon b$
if
![]() $\|a-b\|<\varepsilon $
. Given
$\|a-b\|<\varepsilon $
. Given
![]() $a\in A$
and
$a\in A$
and
![]() $G\subseteq A$
, we write
$G\subseteq A$
, we write
![]() $a\in _\varepsilon G$
if there exists
$a\in _\varepsilon G$
if there exists
![]() $b\in G$
with
$b\in G$
with
![]() $a=_\varepsilon b$
. We use bold letters to denote tuples, for example,
$a=_\varepsilon b$
. We use bold letters to denote tuples, for example,
![]() $\mathbf {a}=(a_1,\ldots ,a_n)\in A^n$
. Given
$\mathbf {a}=(a_1,\ldots ,a_n)\in A^n$
. Given
![]() $\mathbf {a},\mathbf {b}\in A^n$
, we write
$\mathbf {a},\mathbf {b}\in A^n$
, we write
![]() $\mathbf {a}=_\varepsilon \mathbf {b}$
if
$\mathbf {a}=_\varepsilon \mathbf {b}$
if
![]() $a_j=_\varepsilon b_j$
for
$a_j=_\varepsilon b_j$
for
![]() $j=1,\ldots ,n$
. We use
$j=1,\ldots ,n$
. We use
![]() $C^*(\mathbf {a})$
to denote the sub-
$C^*(\mathbf {a})$
to denote the sub-
![]() $C^*\!$
-algebra of A generated by the elements of
$C^*\!$
-algebra of A generated by the elements of
![]() $\mathbf {a}$
. We write
$\mathbf {a}$
. We write
![]() $A^n_{\mathrm {sa}}$
for
$A^n_{\mathrm {sa}}$
for
![]() $(A_{\mathrm {sa}})^n$
, the space of n-tuples of self-adjoint elements in A.
$(A_{\mathrm {sa}})^n$
, the space of n-tuples of self-adjoint elements in A.
2 The generator rank and its precursor
In this section, we briefly recall the definition and basic properties of the generator rank
![]() $\operatorname {\mathrm {gr}}$
and its predecessor
$\operatorname {\mathrm {gr}}$
and its predecessor
![]() $\operatorname {\mathrm {gr}}_0$
from [Reference Thiel and WinterThi21].
$\operatorname {\mathrm {gr}}_0$
from [Reference Thiel and WinterThi21].
Definition 2.1 [Reference Thiel and WinterThi21, Definitions 2.1 and 3.1]
Let A be a
![]() $C^*\!$
-algebra. We define
$C^*\!$
-algebra. We define
![]() $\operatorname {\mathrm {gr}}_0(A)$
as the smallest integer
$\operatorname {\mathrm {gr}}_0(A)$
as the smallest integer
![]() $n\geq 0$
such that for every
$n\geq 0$
such that for every
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
,
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
,
![]() $\varepsilon>0$
, and
$\varepsilon>0$
, and
![]() $c\in A$
, there exists
$c\in A$
, there exists
![]() $\mathbf {b}\in A^{n+1}_{\mathrm {sa}}$
such that
$\mathbf {b}\in A^{n+1}_{\mathrm {sa}}$
such that
If no such n exists, we set
![]() $\operatorname {\mathrm {gr}}_0(A)=\infty $
. The generator rank of A is
$\operatorname {\mathrm {gr}}_0(A)=\infty $
. The generator rank of A is
![]() $\operatorname {\mathrm {gr}}(A):=\operatorname {\mathrm {gr}}_0(\widetilde {A})$
.
$\operatorname {\mathrm {gr}}(A):=\operatorname {\mathrm {gr}}_0(\widetilde {A})$
.
We use
![]() $\operatorname {\mathrm {Gen}}_{n}(A)_{\mathrm {sa}}$
to denote the set of tuples
$\operatorname {\mathrm {Gen}}_{n}(A)_{\mathrm {sa}}$
to denote the set of tuples
![]() $\mathbf {a}\in A^n_{\mathrm {sa}}$
that generate A as a
$\mathbf {a}\in A^n_{\mathrm {sa}}$
that generate A as a
![]() $C^*\!$
-algebra. For separable
$C^*\!$
-algebra. For separable
![]() $C^*\!$
-algebras, the generator rank and its predecessor can be described by the denseness of such tuples.
$C^*\!$
-algebras, the generator rank and its predecessor can be described by the denseness of such tuples.
Theorem 2.2 [Reference Thiel and WinterThi21, Theorem 3.4]
Let A be a separable
![]() $C^*\!$
-algebra and
$C^*\!$
-algebra and
![]() $n\in \mathbb {N}$
. Then:
$n\in \mathbb {N}$
. Then:
-
(1)
 $\operatorname {\mathrm {gr}}_0(A)\leq n$
if and only if
$\operatorname {\mathrm {gr}}_0(A)\leq n$
if and only if
 $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is a dense
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is a dense
 $G_\delta $
-subset.
$G_\delta $
-subset. -
(2)
 $\operatorname {\mathrm {gr}}(A)\leq n$
if and only if
$\operatorname {\mathrm {gr}}(A)\leq n$
if and only if
 $\operatorname {\mathrm {Gen}}_{n+1}(\widetilde {A})_{\mathrm {sa}}\subseteq \widetilde {A}^{n+1}_{\mathrm {sa}}$
is a dense
$\operatorname {\mathrm {Gen}}_{n+1}(\widetilde {A})_{\mathrm {sa}}\subseteq \widetilde {A}^{n+1}_{\mathrm {sa}}$
is a dense
 $G_\delta $
-subset.
$G_\delta $
-subset.
Remark 2.3 Let A be a separable
![]() $C^*\!$
-algebra. If A has generator rank at most one, then the set of (nonself-adjoint) generators in A is a dense
$C^*\!$
-algebra. If A has generator rank at most one, then the set of (nonself-adjoint) generators in A is a dense
![]() $G_\delta $
-subset (see [Reference Thiel and WinterThi21, Remark 3.7]). If A is unital, then the converse also holds: we have
$G_\delta $
-subset (see [Reference Thiel and WinterThi21, Remark 3.7]). If A is unital, then the converse also holds: we have
![]() $\operatorname {\mathrm {gr}}(A)\leq 1$
if and only if a generic element in A is a generator.
$\operatorname {\mathrm {gr}}(A)\leq 1$
if and only if a generic element in A is a generator.
The connection between
![]() $\operatorname {\mathrm {gr}}_0, \operatorname {\mathrm {gr}}$
and the real rank is summarized by the next result, which combines Proposition 3.12 and Theorem 3.13 in [Reference Thiel and WinterThi21]. In Theorem 5.5, we show that
$\operatorname {\mathrm {gr}}_0, \operatorname {\mathrm {gr}}$
and the real rank is summarized by the next result, which combines Proposition 3.12 and Theorem 3.13 in [Reference Thiel and WinterThi21]. In Theorem 5.5, we show that
![]() $\operatorname {\mathrm {gr}}_0$
and
$\operatorname {\mathrm {gr}}_0$
and
![]() $\operatorname {\mathrm {gr}}$
agree for subhomogeneous
$\operatorname {\mathrm {gr}}$
agree for subhomogeneous
![]() $C^*\!$
-algebras. In general, however, it is unclear if
$C^*\!$
-algebras. In general, however, it is unclear if
![]() $\operatorname {\mathrm {gr}}_0=\operatorname {\mathrm {gr}}$
(see [Reference Thiel and WinterThi21, Question 3.16]).
$\operatorname {\mathrm {gr}}_0=\operatorname {\mathrm {gr}}$
(see [Reference Thiel and WinterThi21, Question 3.16]).
Proposition 2.4 Let A be a
![]() $C^*\!$
-algebra. Then,
$C^*\!$
-algebra. Then,
We will frequently use the following permanence properties of
![]() $\operatorname {\mathrm {gr}}_0$
and
$\operatorname {\mathrm {gr}}_0$
and
![]() $\operatorname {\mathrm {gr}}$
, which were shown in Propositions 2.2, 2.7, and 2.9 and Theorem 6.2 in [Reference Thiel and WinterThi21].
$\operatorname {\mathrm {gr}}$
, which were shown in Propositions 2.2, 2.7, and 2.9 and Theorem 6.2 in [Reference Thiel and WinterThi21].
Theorem 2.5 Let A be a
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $I\subseteq A$
be an ideal. Then,
$I\subseteq A$
be an ideal. Then,
and
Recall that a
![]() $C^*\!$
-algebra A is said to be approximated by sub-
$C^*\!$
-algebra A is said to be approximated by sub-
![]() $C^*\!$
-algebras
$C^*\!$
-algebras
![]() $A_\lambda \subseteq A$
if, for every finite subset
$A_\lambda \subseteq A$
if, for every finite subset
![]() $F\subseteq A$
and
$F\subseteq A$
and
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $\lambda $
such that
$\lambda $
such that
![]() $a\in _\varepsilon A_\lambda $
for each
$a\in _\varepsilon A_\lambda $
for each
![]() $a\in F$
. We do not require the subalgebras to be nested. Thus, while
$a\in F$
. We do not require the subalgebras to be nested. Thus, while
![]() $\bigcup _\lambda A_\lambda $
is a dense subset of A, it is not necessarily a subalgebra. The next result combines Propositions 2.3 and 2.4 and Theorem 6.3 in [Reference Thiel and WinterThi21].
$\bigcup _\lambda A_\lambda $
is a dense subset of A, it is not necessarily a subalgebra. The next result combines Propositions 2.3 and 2.4 and Theorem 6.3 in [Reference Thiel and WinterThi21].
Theorem 2.6 Let A be a
![]() $C^*\!$
-algebra that is approximated by sub-
$C^*\!$
-algebra that is approximated by sub-
![]() $C^*\!$
-algebras
$C^*\!$
-algebras
![]() $A_\lambda \subseteq A$
, and let
$A_\lambda \subseteq A$
, and let
![]() $n\in \mathbb {N}$
. If
$n\in \mathbb {N}$
. If
![]() $\operatorname {\mathrm {gr}}_0(A_\lambda )\leq n$
for each
$\operatorname {\mathrm {gr}}_0(A_\lambda )\leq n$
for each
![]() $\lambda $
, then
$\lambda $
, then
![]() $\operatorname {\mathrm {gr}}_0(A)\leq n$
. Analogously, if
$\operatorname {\mathrm {gr}}_0(A)\leq n$
. Analogously, if
![]() $\operatorname {\mathrm {gr}}(A_\lambda )\leq n$
for each
$\operatorname {\mathrm {gr}}(A_\lambda )\leq n$
for each
![]() $\lambda $
, then
$\lambda $
, then
![]() $\operatorname {\mathrm {gr}}(A)\leq n$
.
$\operatorname {\mathrm {gr}}(A)\leq n$
.
Moreover, if
![]() $A=\varinjlim _{j} A_j$
is an inductive limit, then
$A=\varinjlim _{j} A_j$
is an inductive limit, then
Theorem 2.7 [Reference Thiel and WinterThi21, Theorem 5.6]
Let X be a locally compact Hausdorff space. Then,
3 Reduction to the separable case
Let us recall a few concepts from model theory that allow us to reduce some proofs in the following sections to the case of separable
![]() $C^*\!$
-algebras. We refer to [Reference Farah, Hart, Lupini, Robert, Tikuisis, Vignati and WinterFHL+21, Reference Farah and KatsuraFK10] for details.
$C^*\!$
-algebras. We refer to [Reference Farah, Hart, Lupini, Robert, Tikuisis, Vignati and WinterFHL+21, Reference Farah and KatsuraFK10] for details.
3.1. Let A be a
![]() $C^*\!$
-algebra. We use
$C^*\!$
-algebra. We use
![]() $\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
to denote the set of separable sub-
$\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
to denote the set of separable sub-
![]() $C^*\!$
-algebras of A. A collection
$C^*\!$
-algebras of A. A collection
![]() $\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
is said to be
$\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
is said to be
![]() $\sigma $
-complete if we have
$\sigma $
-complete if we have
![]() $\overline {\bigcup \{B:B\in \mathcal {T}\}}\in \mathcal {S}$
for every countable directed subcollection
$\overline {\bigcup \{B:B\in \mathcal {T}\}}\in \mathcal {S}$
for every countable directed subcollection
![]() $\mathcal {T}\subseteq \mathcal {S}$
. Furthermore,
$\mathcal {T}\subseteq \mathcal {S}$
. Furthermore,
![]() $\mathcal {S}$
is said to be cofinal if, for every
$\mathcal {S}$
is said to be cofinal if, for every
![]() $B_0\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
, there is
$B_0\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
, there is
![]() $B\in \mathcal {S}$
such that
$B\in \mathcal {S}$
such that
![]() $B_0\subseteq B$
. It is well known that the intersection of countably many
$B_0\subseteq B$
. It is well known that the intersection of countably many
![]() $\sigma $
-complete, cofinal collections is again
$\sigma $
-complete, cofinal collections is again
![]() $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal.
In [Reference ThielThi13, Definition 1], I formalized the notion of a noncommutative dimension theory as an assignment that to each
![]() $C^*\!$
-algebra A associates a number
$C^*\!$
-algebra A associates a number
![]() $d(A)\in \{0,1,2,\ldots ,\infty \}$
such that six axioms are satisfied. Axioms (D1)–(D4) describe compatibility with passing to ideals, quotients, directs sums, and unitizations. The other axioms are:
$d(A)\in \{0,1,2,\ldots ,\infty \}$
such that six axioms are satisfied. Axioms (D1)–(D4) describe compatibility with passing to ideals, quotients, directs sums, and unitizations. The other axioms are:
-
(D5) If
 $n\in \mathbb {N}$
and if A is a
$n\in \mathbb {N}$
and if A is a
 $C^*\!$
-algebra that is approximated by sub-
$C^*\!$
-algebra that is approximated by sub-
 $C^*\!$
-algebras
$C^*\!$
-algebras
 $A_\lambda \subseteq A$
(as in Theorem 2.6) such that
$A_\lambda \subseteq A$
(as in Theorem 2.6) such that
 $d(A_\lambda )\leq n$
for each
$d(A_\lambda )\leq n$
for each
 $\lambda $
, then
$\lambda $
, then
 $d(A)\leq n$
.
$d(A)\leq n$
. -
(D6) If A is a
 $C^*\!$
-algebra and
$C^*\!$
-algebra and
 $B_0\subseteq A$
is a separable sub-
$B_0\subseteq A$
is a separable sub-
 $C^*\!$
-algebra, then there is a separable sub-
$C^*\!$
-algebra, then there is a separable sub-
 $C^*\!$
-algebra
$C^*\!$
-algebra
 $B\subseteq A$
such that
$B\subseteq A$
such that
 $B_0\subseteq B$
and
$B_0\subseteq B$
and
 $d(B)\leq d(A)$
.
$d(B)\leq d(A)$
.
It was noted in [Reference Thiel and WinterThi21, Paragraph 4.1] that if d is an assignment from
![]() $C^*\!$
-algebras to
$C^*\!$
-algebras to
![]() $\{0,1,\ldots ,\infty \}$
that satisfies (D5) and (D6), then for each
$\{0,1,\ldots ,\infty \}$
that satisfies (D5) and (D6), then for each
![]() $n\in \mathbb {N}$
and each
$n\in \mathbb {N}$
and each
![]() $C^*\!$
-algebra A satisfying
$C^*\!$
-algebra A satisfying
![]() $d(A)\leq n$
, the collection
$d(A)\leq n$
, the collection
is
![]() $\sigma $
-complete and cofinal. It was shown in [Reference Thiel and WinterThi21] that
$\sigma $
-complete and cofinal. It was shown in [Reference Thiel and WinterThi21] that
![]() $\operatorname {\mathrm {gr}}_0$
and
$\operatorname {\mathrm {gr}}_0$
and
![]() $\operatorname {\mathrm {gr}}$
satisfy (D5) and (D6).
$\operatorname {\mathrm {gr}}$
satisfy (D5) and (D6).
Lemma 3.2 Let A be a
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $I\subseteq A$
be an ideal. We have:
$I\subseteq A$
be an ideal. We have:
-
(1) Let
 $\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
be a
$\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
be a
 $\sigma $
-complete and cofinal subcollection. Then, the family
$\sigma $
-complete and cofinal subcollection. Then, the family
 $\{B\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A):B\cap I\in \mathcal {S}\}$
is
$\{B\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A):B\cap I\in \mathcal {S}\}$
is
 $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal. -
(2) Let
 $\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A/I)$
be a
$\mathcal {S}\subseteq \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A/I)$
be a
 $\sigma $
-complete and cofinal subcollection. Then, the family
$\sigma $
-complete and cofinal subcollection. Then, the family
 $\{B\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A):B/(B\cap I)\in \mathcal {S}\}$
is
$\{B\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A):B/(B\cap I)\in \mathcal {S}\}$
is
 $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal.
Proof (1): Set
![]() $\mathcal {T} := \{ B \in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A) : B\cap I \in \mathcal {S} \}$
. It is easy to see that
$\mathcal {T} := \{ B \in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A) : B\cap I \in \mathcal {S} \}$
. It is easy to see that
![]() $\mathcal {T}$
is
$\mathcal {T}$
is
![]() $\sigma $
-complete. To show that it is cofinal, let
$\sigma $
-complete. To show that it is cofinal, let
![]() $B_0\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
. We will inductively find increasing sequences
$B_0\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
. We will inductively find increasing sequences
![]() $(I_k)_k$
in
$(I_k)_k$
in
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $(B_k)_k$
in
$(B_k)_k$
in
![]() $\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
such that
$\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
such that
Assume that we have obtained
![]() $B_k$
for some
$B_k$
for some
![]() $k\in \mathbb {N}$
. Then,
$k\in \mathbb {N}$
. Then,
![]() $B_k\cap I\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
, and since
$B_k\cap I\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
, and since
![]() $\mathcal {S}$
is cofinal in
$\mathcal {S}$
is cofinal in
![]() $\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
, we obtain
$\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(I)$
, we obtain
![]() $I_k\in \mathcal {S}$
such that
$I_k\in \mathcal {S}$
such that
![]() $B_k\cap I\subseteq I_k$
. Then, let
$B_k\cap I\subseteq I_k$
. Then, let
![]() $B_{k+1}$
be the sub-
$B_{k+1}$
be the sub-
![]() $C^*\!$
-algebra of A generated by
$C^*\!$
-algebra of A generated by
![]() $B_k$
and
$B_k$
and
![]() $I_k$
.
$I_k$
.
Set
![]() $B:=\overline {\bigcup _k B_k}$
, which belongs to
$B:=\overline {\bigcup _k B_k}$
, which belongs to
![]() $\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
and contains
$\operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A)$
and contains
![]() $B_0$
. We have
$B_0$
. We have
![]() $B\cap I = \overline {\bigcup _k I_k}$
. Since
$B\cap I = \overline {\bigcup _k I_k}$
. Since
![]() $\mathcal {S}$
is
$\mathcal {S}$
is
![]() $\sigma $
-complete,
$\sigma $
-complete,
![]() $B\cap I$
belongs to
$B\cap I$
belongs to
![]() $\mathcal {S}$
. Thus, B belongs to
$\mathcal {S}$
. Thus, B belongs to
![]() $\mathcal {T}$
, as desired.
$\mathcal {T}$
, as desired.
Statement (2) is shown similarly.
3.3. Recall that a
![]() $C^*\!$
-algebra is called d-homogeneous (for some
$C^*\!$
-algebra is called d-homogeneous (for some
![]() $d\geq 1$
) if all its irreducible representations are d-dimensional, and it is called homogeneous if it is d-homogeneous for some d (see [Reference BlackadarBla06, Definition IV.1.4.1, p. 330]).
$d\geq 1$
) if all its irreducible representations are d-dimensional, and it is called homogeneous if it is d-homogeneous for some d (see [Reference BlackadarBla06, Definition IV.1.4.1, p. 330]).
Let A be a d-homogeneous
![]() $C^*\!$
-algebra, and set
$C^*\!$
-algebra, and set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
, the primitive ideal space of A. Then, X is a locally compact Hausdorff space, and there exists a locally trivial bundle over X with fiber
$X:=\operatorname {\mathrm {Prim}}(A)$
, the primitive ideal space of A. Then, X is a locally compact Hausdorff space, and there exists a locally trivial bundle over X with fiber
![]() $M_d$
such that A is canonically isomorphic to the algebra of continuous cross sections vanishing at infinity, with pointwise operations (see [Reference FellFel61, Theorem 3.2]).
$M_d$
such that A is canonically isomorphic to the algebra of continuous cross sections vanishing at infinity, with pointwise operations (see [Reference FellFel61, Theorem 3.2]).
It follows that the center of A is canonically isomorphic to
![]() $C_0(X)$
, and this gives A the structure of a continuous
$C_0(X)$
, and this gives A the structure of a continuous
![]() $C_0(X)$
-algebra, with each fiber isomorphic to
$C_0(X)$
-algebra, with each fiber isomorphic to
![]() $M_d$
. For the definition and results of
$M_d$
. For the definition and results of
![]() $C_{0}(X)$
-algebras, we refer the reader to Section 2 of [Reference DadarlatDad09]. Given a
$C_{0}(X)$
-algebras, we refer the reader to Section 2 of [Reference DadarlatDad09]. Given a
![]() $C_0(X)$
-algebra A and a closed subset
$C_0(X)$
-algebra A and a closed subset
![]() $Y\subseteq X$
, we let
$Y\subseteq X$
, we let
![]() $A(Y)$
denote the quotient of A corresponding to Y. The fiber of A at
$A(Y)$
denote the quotient of A corresponding to Y. The fiber of A at
![]() $x\in X$
is
$x\in X$
is
![]() $A(x):=A(\{x\})$
. Given
$A(x):=A(\{x\})$
. Given
![]() $a\in A$
and
$a\in A$
and
![]() $x\in X$
, we write
$x\in X$
, we write
![]() $a(x)$
for the image of a in the quotient
$a(x)$
for the image of a in the quotient
![]() $A(x)$
. Given
$A(x)$
. Given
![]() $\mathbf {a}=(a_0,\ldots ,a_n)\in A^{n+1}$
, we set
$\mathbf {a}=(a_0,\ldots ,a_n)\in A^{n+1}$
, we set
![]() $\mathbf {a}(x):=(a_0(x),\ldots ,a_n(x))\in A(x)^{n+1}$
.
$\mathbf {a}(x):=(a_0(x),\ldots ,a_n(x))\in A(x)^{n+1}$
.
Given a locally compact Hausdorff space X, the local dimension of X is
with the convention that
![]() $\operatorname {\mathrm {locdim}}(\emptyset )=-1$
. As noted in [Reference Thiel and WinterThi21, Paragraph 5.5], if X is nonempty, then
$\operatorname {\mathrm {locdim}}(\emptyset )=-1$
. As noted in [Reference Thiel and WinterThi21, Paragraph 5.5], if X is nonempty, then
![]() $\operatorname {\mathrm {locdim}}(X)$
agrees with the dimension of the one-point compactification of X. If X is
$\operatorname {\mathrm {locdim}}(X)$
agrees with the dimension of the one-point compactification of X. If X is
![]() $\sigma $
-compact, then
$\sigma $
-compact, then
![]() $\dim (X)=\operatorname {\mathrm {locdim}}(X)$
.
$\dim (X)=\operatorname {\mathrm {locdim}}(X)$
.
Lemma 3.4 Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $l\in \mathbb {N}$
, and let X be a compact Hausdorff space satisfying
$l\in \mathbb {N}$
, and let X be a compact Hausdorff space satisfying
![]() $\dim (X)\leq l$
. Set
$\dim (X)\leq l$
. Set
![]() $A:=C(X,M_d)$
. Then,
$A:=C(X,M_d)$
. Then,
is
![]() $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal.
Proof
![]() $\sigma $
-completeness: Let
$\sigma $
-completeness: Let
![]() $\mathcal {T}\subseteq \mathcal {S}$
be a countable directed family, and set
$\mathcal {T}\subseteq \mathcal {S}$
be a countable directed family, and set
![]() $C:=\overline {\bigcup \{B:B\in \mathcal {T}\}}$
. To show that C is d-homogeneous, let
$C:=\overline {\bigcup \{B:B\in \mathcal {T}\}}$
. To show that C is d-homogeneous, let
![]() $\varrho $
be an irreducible representation of C. Since C is d-subhomogeneous (as a subalgebra of A), the dimension of
$\varrho $
be an irreducible representation of C. Since C is d-subhomogeneous (as a subalgebra of A), the dimension of
![]() $\varrho $
is at most d. If
$\varrho $
is at most d. If
![]() $\dim (\varrho )<d$
, then the restriction of
$\dim (\varrho )<d$
, then the restriction of
![]() $\varrho $
to each
$\varrho $
to each
![]() $B\in \mathcal {T}$
is zero, whence
$B\in \mathcal {T}$
is zero, whence
![]() $\varrho =0$
, a contradiction.
$\varrho =0$
, a contradiction.
In [Reference Brown and PedersenBP09, Section 2.2], Brown and Pedersen introduce the topological dimension of type
![]() $\mathrm {I} C^*\!$
-algebras. Given a homogeneous
$\mathrm {I} C^*\!$
-algebras. Given a homogeneous
![]() $C^*\!$
-algebra D, the topological dimension
$C^*\!$
-algebra D, the topological dimension
![]() $\operatorname {\mathrm {topdim}}(D)$
is equal to
$\operatorname {\mathrm {topdim}}(D)$
is equal to
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(D))$
. Hence, each
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(D))$
. Hence, each
![]() $B\in \mathcal {T}$
satisfies
$B\in \mathcal {T}$
satisfies
![]() $\operatorname {\mathrm {topdim}}(B)=\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))\leq l$
. By [Reference ThielThi13, Lemma 3], a continuous trace
$\operatorname {\mathrm {topdim}}(B)=\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))\leq l$
. By [Reference ThielThi13, Lemma 3], a continuous trace
![]() $C^*\!$
-algebra (in particular, a homogeneous
$C^*\!$
-algebra (in particular, a homogeneous
![]() $C^*\!$
-algebra) has topological dimension at most l whenever it is approximated by sub-
$C^*\!$
-algebra) has topological dimension at most l whenever it is approximated by sub-
![]() $C^*\!$
-algebras with topological dimension at most l. Hence,
$C^*\!$
-algebras with topological dimension at most l. Hence,
which verifies that C belongs to
![]() $\mathcal {S}$
, as desired.
$\mathcal {S}$
, as desired.
Cofinality: Let
![]() $B_0\subseteq A$
be a separable sub-
$B_0\subseteq A$
be a separable sub-
![]() $C^*\!$
-algebra. We identify A with
$C^*\!$
-algebra. We identify A with
![]() $C(X)\otimes M_d$
. Let
$C(X)\otimes M_d$
. Let
![]() $e_{jk}\in M_d$
,
$e_{jk}\in M_d$
,
![]() $j,k=1,\ldots ,d$
, be matrix units. Let
$j,k=1,\ldots ,d$
, be matrix units. Let
![]() $C(Y)\subseteq C(X)$
be a separable, unital sub-
$C(Y)\subseteq C(X)$
be a separable, unital sub-
![]() $C^*\!$
-algebra such that
$C^*\!$
-algebra such that
![]() $f\in C(X)$
belongs to
$f\in C(X)$
belongs to
![]() $C(Y)$
whenever
$C(Y)$
whenever
![]() $f\otimes e_{jk}\in B_0$
for some
$f\otimes e_{jk}\in B_0$
for some
![]() $j,k$
. Using that the real rank satisfies (D6), let
$j,k$
. Using that the real rank satisfies (D6), let
![]() $C(Z)\subseteq C(X)$
be a separable sub-
$C(Z)\subseteq C(X)$
be a separable sub-
![]() $C^*\!$
-algebra containing
$C^*\!$
-algebra containing
![]() $C(Y)$
such that
$C(Y)$
such that
![]() $\operatorname {\mathrm {rr}}(C(Z))\leq \operatorname {\mathrm {rr}}(C(X))$
. Then,
$\operatorname {\mathrm {rr}}(C(Z))\leq \operatorname {\mathrm {rr}}(C(X))$
. Then,
and it follows that
![]() $C(Z)\otimes M_d\subseteq C(X)\otimes M_d$
has the desired properties.
$C(Z)\otimes M_d\subseteq C(X)\otimes M_d$
has the desired properties.
Proposition 3.5 Let
![]() $d\geq 1$
,
$d\geq 1$
,
![]() $l\in \mathbb {N}$
, and let A be a d-homogeneous
$l\in \mathbb {N}$
, and let A be a d-homogeneous
![]() $C^*\!$
-algebra satisfying
$C^*\!$
-algebra satisfying
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(A))\leq l$
. Then,
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(A))\leq l$
. Then,
is
![]() $\sigma $
-complete and cofinal.
$\sigma $
-complete and cofinal.
Proof As in the proof of Lemma 3.4, we obtain that
![]() $\mathcal {S}$
is
$\mathcal {S}$
is
![]() $\sigma $
-complete.
$\sigma $
-complete.
Cofinality: Let
![]() $B_0\subseteq A$
be a separable sub-
$B_0\subseteq A$
be a separable sub-
![]() $C^*\!$
-algebra. Let
$C^*\!$
-algebra. Let
![]() $I\subseteq A$
be the ideal generated by
$I\subseteq A$
be the ideal generated by
![]() $B_0$
. Then, I is d-homogeneous and
$B_0$
. Then, I is d-homogeneous and
![]() $X:=\operatorname {\mathrm {Prim}}(I)$
is
$X:=\operatorname {\mathrm {Prim}}(I)$
is
![]() $\sigma $
-compact. We view I as a
$\sigma $
-compact. We view I as a
![]() $C_0(X)$
-algebra with all fibers isomorphic to
$C_0(X)$
-algebra with all fibers isomorphic to
![]() $M_d$
. Since the
$M_d$
. Since the
![]() $M_d$
-bundle associated with I is locally trivial, and since X is
$M_d$
-bundle associated with I is locally trivial, and since X is
![]() $\sigma $
-compact, we can choose a sequence of compact subsets
$\sigma $
-compact, we can choose a sequence of compact subsets
![]() $X_0,X_1,X_2,\ldots \subseteq X$
that cover X such that
$X_0,X_1,X_2,\ldots \subseteq X$
that cover X such that
![]() $I(X_j)\cong C(X_j)\otimes M_d$
for each
$I(X_j)\cong C(X_j)\otimes M_d$
for each
![]() $j\in \mathbb {N}$
.
$j\in \mathbb {N}$
.
Given j, let
![]() $\pi _j\colon I\to C(X_j)\otimes M_d$
be the corresponding quotient map, and set
$\pi _j\colon I\to C(X_j)\otimes M_d$
be the corresponding quotient map, and set
Applying Lemmas 3.2(2) and 3.4, we obtain that
![]() $\mathcal {S}_j$
is
$\mathcal {S}_j$
is
![]() $\sigma $
-complete and cofinal. It follows that
$\sigma $
-complete and cofinal. It follows that
![]() $\mathcal {S}:=\bigcap _{j=0}^\infty \mathcal {S}_j$
is
$\mathcal {S}:=\bigcap _{j=0}^\infty \mathcal {S}_j$
is
![]() $\sigma $
-complete and cofinal as well. Choose
$\sigma $
-complete and cofinal as well. Choose
![]() $B\in \mathcal {S}$
satisfying
$B\in \mathcal {S}$
satisfying
![]() $B_0\subseteq B$
.
$B_0\subseteq B$
.
To verify that B is d-homogeneous, let
![]() $\varrho $
be an irreducible representation of B. Since B is d-subhomogeneous, we have
$\varrho $
be an irreducible representation of B. Since B is d-subhomogeneous, we have
![]() $\dim (\varrho )\leq d$
. Extend
$\dim (\varrho )\leq d$
. Extend
![]() $\varrho $
to an irreducible representation
$\varrho $
to an irreducible representation
![]() $\varrho '$
of I (a priori on a possibly larger Hilbert space). Then, there exists
$\varrho '$
of I (a priori on a possibly larger Hilbert space). Then, there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $\varrho '$
is isomorphic to the quotient map to the fiber at x. Let
$\varrho '$
is isomorphic to the quotient map to the fiber at x. Let
![]() $j\in \mathbb {N}$
such that
$j\in \mathbb {N}$
such that
![]() $x\in X_j$
. Since B belongs to
$x\in X_j$
. Since B belongs to
![]() $\mathcal {S}_j$
, it exhausts the fiber at x, and we deduce that
$\mathcal {S}_j$
, it exhausts the fiber at x, and we deduce that
![]() $\dim (\varrho )\geq d$
.
$\dim (\varrho )\geq d$
.
To see that
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))\leq l$
, let
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))\leq l$
, let
![]() $K\subseteq \operatorname {\mathrm {Prim}}(B)$
be a compact subset. For each j, let
$K\subseteq \operatorname {\mathrm {Prim}}(B)$
be a compact subset. For each j, let
![]() $F_j\subseteq \operatorname {\mathrm {Prim}}(B)$
be the closed subset corresponding to the quotient
$F_j\subseteq \operatorname {\mathrm {Prim}}(B)$
be the closed subset corresponding to the quotient
![]() $\pi _j(B)$
of B. Since B belongs to
$\pi _j(B)$
of B. Since B belongs to
![]() $\mathcal {S}_j$
, we have
$\mathcal {S}_j$
, we have
![]() $\operatorname {\mathrm {locdim}}(F_j)\leq l$
. Hence,
$\operatorname {\mathrm {locdim}}(F_j)\leq l$
. Hence,
![]() $\dim (K\cap F_j)\leq l$
. We have
$\dim (K\cap F_j)\leq l$
. We have
![]() $K=\bigcup _j (K\cap F_j)$
, and therefore
$K=\bigcup _j (K\cap F_j)$
, and therefore
by the Countable Sum Theorem (see [Reference PhillipsPea75, Theorem 3.2.5, p. 125]; see also the introduction to Section 5).
4 Homogeneous
 $C^*\!$
-algebras
$C^*\!$
-algebras
In this section, we compute the generator rank of homogeneous
![]() $C^*\!$
-algebra; (see Theorem 4.17). We first consider the unital separable case (Lemma 4.15), we then generalize to the unital nonseparable case (Proposition 4.16) and finally to the general case. Unlike for commutative
$C^*\!$
-algebra; (see Theorem 4.17). We first consider the unital separable case (Lemma 4.15), we then generalize to the unital nonseparable case (Proposition 4.16) and finally to the general case. Unlike for commutative
![]() $C^*\!$
-algebras, the unital separable case is highly nontrivial and it requires a delicate analysis of the codimension of certain submanifolds of
$C^*\!$
-algebras, the unital separable case is highly nontrivial and it requires a delicate analysis of the codimension of certain submanifolds of
![]() $(M_d)^{n+1}_{\mathrm {sa}}$
(Lemma 4.11) in connection with a suitable version of the homotopy extension lifting property (Lemma 4.14).
$(M_d)^{n+1}_{\mathrm {sa}}$
(Lemma 4.11) in connection with a suitable version of the homotopy extension lifting property (Lemma 4.14).
The next result characterizes generating tuples in separable
![]() $C(X)$
-algebras with simple fibers, and thus in particular in unital, separable, homogeneous
$C(X)$
-algebras with simple fibers, and thus in particular in unital, separable, homogeneous
![]() $C^*\!$
-algebras. Given a map
$C^*\!$
-algebras. Given a map
![]() $\varphi \colon D\to E$
between
$\varphi \colon D\to E$
between
![]() $C^*\!$
-algebras and
$C^*\!$
-algebras and
![]() $\mathbf {a}=(a_0,\ldots ,a_n)\in D^{n+1}$
, we set
$\mathbf {a}=(a_0,\ldots ,a_n)\in D^{n+1}$
, we set
Proposition 4.1 Let X be a compact metric space, and let A be a separable
![]() $C(X)$
-algebra such that all fibers are simple. Let
$C(X)$
-algebra such that all fibers are simple. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
. Then,
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
. Then,
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if the following are satisfied:
$\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if the following are satisfied:
-
(a)
 $\mathbf {a}$
generates each fiber, that is,
$\mathbf {a}$
generates each fiber, that is,
 $\mathbf {a}(x)\in \operatorname {\mathrm {Gen}}_{n+1}(A(x))_{\mathrm {sa}}$
for each
$\mathbf {a}(x)\in \operatorname {\mathrm {Gen}}_{n+1}(A(x))_{\mathrm {sa}}$
for each
 $x\in X$
.
$x\in X$
. -
(b)
 $\mathbf {a}$
separates the points of X in the sense that for distinct
$\mathbf {a}$
separates the points of X in the sense that for distinct
 $x,y\in X$
, there is no isomorphism
$x,y\in X$
, there is no isomorphism
 $\alpha \colon A(x)\to A(y)$
satisfying
$\alpha \colon A(x)\to A(y)$
satisfying
 $\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
.
$\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
.
Proof Let us first assume that
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
. For
$\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
. For
![]() $x\in X$
, let
$x\in X$
, let
![]() $\pi _x\colon A\to A(x)$
be the quotient map onto the fiber at x. Since
$\pi _x\colon A\to A(x)$
be the quotient map onto the fiber at x. Since
![]() $\pi _x$
is a surjective
$\pi _x$
is a surjective
![]() ${}^*$
-homomorphism, it maps
${}^*$
-homomorphism, it maps
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
to
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
to
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A(x))_{\mathrm {sa}}$
, which verifies (a). Similarly, for distinct points
$\operatorname {\mathrm {Gen}}_{n+1}(A(x))_{\mathrm {sa}}$
, which verifies (a). Similarly, for distinct points
![]() $x,y\in X$
, the map
$x,y\in X$
, the map
![]() $\pi _x\oplus \pi _y\colon A\to A(x)\oplus A(y)$
is a surjective
$\pi _x\oplus \pi _y\colon A\to A(x)\oplus A(y)$
is a surjective
![]() ${}^*$
-homomorphism. It follows that
${}^*$
-homomorphism. It follows that
![]() $(\mathbf {a}(x),\mathbf {a}(y))=(\pi _x\oplus \pi _y)(\mathbf {a})\in \operatorname {\mathrm {Gen}}_{n+1}(A(x)\oplus A(y))_{\mathrm {sa}}$
. To verify (b), assume that
$(\mathbf {a}(x),\mathbf {a}(y))=(\pi _x\oplus \pi _y)(\mathbf {a})\in \operatorname {\mathrm {Gen}}_{n+1}(A(x)\oplus A(y))_{\mathrm {sa}}$
. To verify (b), assume that
![]() $\alpha \colon A(x)\to A(y)$
is an isomorphism satisfying
$\alpha \colon A(x)\to A(y)$
is an isomorphism satisfying
![]() $\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
. Then,
$\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
. Then,
which contradicts that
![]() $(\mathbf {a}(x),\mathbf {a}(y))$
generates
$(\mathbf {a}(x),\mathbf {a}(y))$
generates
![]() $A(x)\oplus A(y)$
. Thus, no such
$A(x)\oplus A(y)$
. Thus, no such
![]() $\alpha $
exists.
$\alpha $
exists.
Conversely, let us assume that (a) and (b) are satisfied. Set
![]() $B:=C^*(\mathbf {a})$
. We need to prove
$B:=C^*(\mathbf {a})$
. We need to prove
![]() $B=A$
. This follows from [Reference Tikuisis, White and WinterTW14, Lemma 3.2] once we show that B exhausts the fiber
$B=A$
. This follows from [Reference Tikuisis, White and WinterTW14, Lemma 3.2] once we show that B exhausts the fiber
![]() $A(x)$
for each
$A(x)$
for each
![]() $x\in X$
, and that for distinct
$x\in X$
, and that for distinct
![]() $x,y\in X$
, there exists
$x,y\in X$
, there exists
![]() $b\in B$
such that
$b\in B$
such that
![]() $b(x)$
is full in
$b(x)$
is full in
![]() $A(x)$
and
$A(x)$
and
![]() $b(y)=0$
. The exhaustion of fibers follows directly from (a).
$b(y)=0$
. The exhaustion of fibers follows directly from (a).
Let
![]() $x,y\in X$
be distinct, and set
$x,y\in X$
be distinct, and set
![]() $C:=(\pi _x\oplus \pi _y)(B)\subseteq A(x)\oplus A(y)$
. Note that C is the sub-
$C:=(\pi _x\oplus \pi _y)(B)\subseteq A(x)\oplus A(y)$
. Note that C is the sub-
![]() $C^*\!$
-algebra of
$C^*\!$
-algebra of
![]() $A(x)\oplus A(y)$
generated by
$A(x)\oplus A(y)$
generated by
![]() $(\mathbf {a}(x),\mathbf {a}(y))$
. If
$(\mathbf {a}(x),\mathbf {a}(y))$
. If
![]() $C\neq A(x)\oplus A(y)$
, using that
$C\neq A(x)\oplus A(y)$
, using that
![]() $A(x)$
and
$A(x)$
and
![]() $A(y)$
are simple, it follows from [Reference Thiel and WinterThi21, Lemma 5.10] that there exists an isomorphism
$A(y)$
are simple, it follows from [Reference Thiel and WinterThi21, Lemma 5.10] that there exists an isomorphism
![]() $\alpha \colon A(x)\to A(y)$
such that
$\alpha \colon A(x)\to A(y)$
such that
which implies that
![]() $\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
. Since this contradicts (b), we deduce that
$\alpha (\mathbf {a}(x))=\mathbf {a}(y)$
. Since this contradicts (b), we deduce that
![]() $C=A(x)\oplus A(y)$
. Hence, there exists
$C=A(x)\oplus A(y)$
. Hence, there exists
![]() $b\in B$
such that
$b\in B$
such that
![]() $b(x)$
is full in
$b(x)$
is full in
![]() $A(x)$
and
$A(x)$
and
![]() $b(y)=0$
.
$b(y)=0$
.
Notation 4.2 For
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $n\in \mathbb {N}$
, we set
$n\in \mathbb {N}$
, we set
Note that
![]() $E_d^{n+1}$
is isomorphic to
$E_d^{n+1}$
is isomorphic to
![]() $\mathbb {R}^{(n+1)d^2}$
as topological vector spaces. In particular,
$\mathbb {R}^{(n+1)d^2}$
as topological vector spaces. In particular,
![]() $E_d^{n+1}$
is a (real) manifold with
$E_d^{n+1}$
is a (real) manifold with
![]() $\dim (E_d^{n+1})=(n+1)d^2$
.
$\dim (E_d^{n+1})=(n+1)d^2$
.
We let
![]() ${\mathcal {U}}_d$
denote the unitary group of
${\mathcal {U}}_d$
denote the unitary group of
![]() $M_d$
. It is a compact Lie group of dimension
$M_d$
. It is a compact Lie group of dimension
![]() $d^2$
. Every automorphism of
$d^2$
. Every automorphism of
![]() $M_d$
is inner, and the kernel of
$M_d$
is inner, and the kernel of
![]() ${\mathcal {U}}_d\to \operatorname {\mathrm {Aut}}(M_d)$
is the group of central unitaries
${\mathcal {U}}_d\to \operatorname {\mathrm {Aut}}(M_d)$
is the group of central unitaries
![]() $\mathbb {T} 1\subseteq {\mathcal {U}}_d$
. Hence,
$\mathbb {T} 1\subseteq {\mathcal {U}}_d$
. Hence,
![]() $\operatorname {\mathrm {Aut}}(M_d)$
is naturally isomorphic to
$\operatorname {\mathrm {Aut}}(M_d)$
is naturally isomorphic to
![]() $\mathcal {PU}_d:={\mathcal {U}}_d/(\mathbb {T} 1)$
, the projective unitary group, which is a compact Lie group of dimension
$\mathcal {PU}_d:={\mathcal {U}}_d/(\mathbb {T} 1)$
, the projective unitary group, which is a compact Lie group of dimension
![]() $d^2-1$
. Given
$d^2-1$
. Given
![]() $u\in {\mathcal {U}}_d$
, we use
$u\in {\mathcal {U}}_d$
, we use
![]() $[u]$
to denote its class in
$[u]$
to denote its class in
![]() $\mathcal {PU}_d$
.
$\mathcal {PU}_d$
.
The action
![]() $\mathcal {PU}_d\curvearrowright M_d$
induces an action
$\mathcal {PU}_d\curvearrowright M_d$
induces an action
![]() $\mathcal {PU}_d\curvearrowright E_d^{n+1}$
by setting
$\mathcal {PU}_d\curvearrowright E_d^{n+1}$
by setting
for
![]() $u\in {\mathcal {U}}_d$
and
$u\in {\mathcal {U}}_d$
and
![]() $\mathbf {a}=(a_0,\ldots ,a_n)\in E_d^{n+1}$
.
$\mathbf {a}=(a_0,\ldots ,a_n)\in E_d^{n+1}$
.
4.3. Let A be a unital, separable, d-homogeneous
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $n\in \mathbb {N}$
. Set
$n\in \mathbb {N}$
. Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. We consider A with its canonical
$X:=\operatorname {\mathrm {Prim}}(A)$
. We consider A with its canonical
![]() $C(X)$
-algebra structure, with each fiber isomorphic to
$C(X)$
-algebra structure, with each fiber isomorphic to
![]() $M_d$
(see Paragraph 3.3). Set
$M_d$
(see Paragraph 3.3). Set
Given
![]() $x\in X$
, let
$x\in X$
, let
![]() $\pi _x\colon A\to A(x)$
denote the map to the fiber at x. This induces a map
$\pi _x\colon A\to A(x)$
denote the map to the fiber at x. This induces a map
![]() $A^{n+1}_{\mathrm {sa}}\to (A(x))^{n+1}_{\mathrm {sa}}$
, which we also denote by
$A^{n+1}_{\mathrm {sa}}\to (A(x))^{n+1}_{\mathrm {sa}}$
, which we also denote by
![]() $\pi _x$
. Choose an isomorphism
$\pi _x$
. Choose an isomorphism
![]() $A(x)\cong M_d$
, which induces an isomorphism
$A(x)\cong M_d$
, which induces an isomorphism
![]() $(A(x))^{n+1}_{\mathrm {sa}} \cong E^{n+1}_d = (M_d)^{n+1}_{\mathrm {sa}}$
. Since the isomorphism
$(A(x))^{n+1}_{\mathrm {sa}} \cong E^{n+1}_d = (M_d)^{n+1}_{\mathrm {sa}}$
. Since the isomorphism
![]() $A(x)\cong M_d$
is unique up to an automorphism of
$A(x)\cong M_d$
is unique up to an automorphism of
![]() $M_d$
, we obtain a canonical homeomorphism
$M_d$
, we obtain a canonical homeomorphism
![]() $(A(x))^{n+1}_{\mathrm {sa}}/\operatorname {\mathrm {Aut}}(A(x)) \cong E^{n+1}_d / \mathcal {PU}_d$
. We let
$(A(x))^{n+1}_{\mathrm {sa}}/\operatorname {\mathrm {Aut}}(A(x)) \cong E^{n+1}_d / \mathcal {PU}_d$
. We let
![]() $\psi _x\colon A^{n+1}_{\mathrm {sa}}\to E^{n+1}_d/\mathcal {PU}_d$
be the resulting natural map.
$\psi _x\colon A^{n+1}_{\mathrm {sa}}\to E^{n+1}_d/\mathcal {PU}_d$
be the resulting natural map.
Given
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
, one checks that
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
, one checks that
![]() $\psi _x(\mathbf {a})$
depends continuously on x. This allows us to define
$\psi _x(\mathbf {a})$
depends continuously on x. This allows us to define
![]() $\Psi \colon A^{n+1}_{\mathrm {sa}}\to C(X,E^{n+1}_d/\mathcal {PU}_d)$
by
$\Psi \colon A^{n+1}_{\mathrm {sa}}\to C(X,E^{n+1}_d/\mathcal {PU}_d)$
by
for
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
and
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
and
![]() $x\in X$
. Restricting
$x\in X$
. Restricting
![]() $\Psi $
to
$\Psi $
to
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
gives a continuous map
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
gives a continuous map
We let
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
denote the set of continuous maps
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
denote the set of continuous maps
![]() $X\to G^{n+1}_d/\mathcal {PU}_d$
that are injective. By Proposition 4.1, a tuple
$X\to G^{n+1}_d/\mathcal {PU}_d$
that are injective. By Proposition 4.1, a tuple
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
belongs to
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
belongs to
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if (a):
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if (a):
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, and (b):
$\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, and (b):
![]() $\Psi (\mathbf {a})\in E(X,G^{n+1}_d/\mathcal {PU}_d)$
. Thus, to determine the generator rank of A, we need to answer the following questions:
$\Psi (\mathbf {a})\in E(X,G^{n+1}_d/\mathcal {PU}_d)$
. Thus, to determine the generator rank of A, we need to answer the following questions:
-
(a) When is
 $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
dense in
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
dense in
 $A^{n+1}_{\mathrm {sa}}$
?
$A^{n+1}_{\mathrm {sa}}$
? -
(b) When is
 $E(X,G_d^{n+1}/\mathcal {PU}_d)$
dense in
$E(X,G_d^{n+1}/\mathcal {PU}_d)$
dense in
 $C(X,G_d^{n+1}/\mathcal {PU}_d)$
?
$C(X,G_d^{n+1}/\mathcal {PU}_d)$
?
Analogous as for the computation of the generator rank for unital, separable, commutative
![]() $C^*\!$
-algebras in [Reference Thiel and WinterThi21, Section 5], the answer to question (a) is determined by
$C^*\!$
-algebras in [Reference Thiel and WinterThi21, Section 5], the answer to question (a) is determined by
![]() $\dim (X)$
, and the answer to (b) is determined by
$\dim (X)$
, and the answer to (b) is determined by
![]() $\dim (X\times X)$
. However, while in the commutative case the dominating condition was (b) involving
$\dim (X\times X)$
. However, while in the commutative case the dominating condition was (b) involving
![]() $\dim (X\times X)$
, we will see that for d-homogeneous
$\dim (X\times X)$
, we will see that for d-homogeneous
![]() $C^*\!$
-algebras with
$C^*\!$
-algebras with
![]() $d\geq 2$
the dominating condition is (a) involving
$d\geq 2$
the dominating condition is (a) involving
![]() $\dim (X)$
.
$\dim (X)$
.
To study (a), we will determine the dimension of
![]() $E^{n+1}_d\setminus G^{n+1}_d$
. For this, we study the action
$E^{n+1}_d\setminus G^{n+1}_d$
. For this, we study the action
![]() $\mathcal {PU}_d\curvearrowright E_d^{n+1}$
. We will show that
$\mathcal {PU}_d\curvearrowright E_d^{n+1}$
. We will show that
![]() $G^{n+1}_d$
consists precisely of the tuples in
$G^{n+1}_d$
consists precisely of the tuples in
![]() $E_d^{n+1}$
with trivial stabilizer subgroup (see Lemma 4.7). This allows us to describe
$E_d^{n+1}$
with trivial stabilizer subgroup (see Lemma 4.7). This allows us to describe
![]() $E^{n+1}_d\setminus G^{n+1}_d$
as the union of the submanifolds corresponding to nontrivial stabilizer subgroups. We then estimate the dimension of these submanifolds (see Lemma 4.11).
$E^{n+1}_d\setminus G^{n+1}_d$
as the union of the submanifolds corresponding to nontrivial stabilizer subgroups. We then estimate the dimension of these submanifolds (see Lemma 4.11).
To study (b), we show that
![]() $G_d^{n+1}$
is an open subset of
$G_d^{n+1}$
is an open subset of
![]() $E_d^{n+1}$
(see Lemma 4.9). Hence,
$E_d^{n+1}$
(see Lemma 4.9). Hence,
![]() $G_d^{n+1}$
is a manifold with
$G_d^{n+1}$
is a manifold with
![]() $\dim (G_d^{n+1})=\dim (E_d^{n+1})=(n+1)d^2$
. We let
$\dim (G_d^{n+1})=\dim (E_d^{n+1})=(n+1)d^2$
. We let
![]() $G_d^{n+1}/\mathcal {PU}_d$
denote the quotient space. Since
$G_d^{n+1}/\mathcal {PU}_d$
denote the quotient space. Since
![]() $\mathcal {PU}_d$
is a compact Lie group of dimension
$\mathcal {PU}_d$
is a compact Lie group of dimension
![]() $d^2-1$
, it follows that
$d^2-1$
, it follows that
![]() $G_d^{n+1}/\mathcal {PU}_d$
is a manifold of dimension
$G_d^{n+1}/\mathcal {PU}_d$
is a manifold of dimension
![]() $(n+1)d^2-(d^2-1)=nd^2+1$
. We then use a result of [Reference LuukkainenLuu81] which characterizes when a continuous map to a manifold can be approximated by injective maps.
$(n+1)d^2-(d^2-1)=nd^2+1$
. We then use a result of [Reference LuukkainenLuu81] which characterizes when a continuous map to a manifold can be approximated by injective maps.
Finally, we use a version of the homotopy extension lifting property for the projection
![]() $G_d^{n+1}\to G_d^{n+1}/\mathcal {PU}_d$
(see Lemma 4.14) to show that a given tuple in
$G_d^{n+1}\to G_d^{n+1}/\mathcal {PU}_d$
(see Lemma 4.14) to show that a given tuple in
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
can be approximated by tuples that are mapped to
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
can be approximated by tuples that are mapped to
![]() $E(X,G_d^{n+1}/\mathcal {PU}_d)$
by
$E(X,G_d^{n+1}/\mathcal {PU}_d)$
by
![]() $\Psi $
.
$\Psi $
.
4.4. Let G be a compact Lie group, acting smoothly on a connected manifold M. We briefly recall the orbit-type decomposition. For details, we refer the reader to [Reference BredonBre72, Reference MeinrekenMei03]. We will later apply this for the action
![]() $\mathcal {PU}_d\curvearrowright E^{n+1}_d$
.
$\mathcal {PU}_d\curvearrowright E^{n+1}_d$
.
The stabilizer subgroup of
![]() $m\in M$
is
$m\in M$
is
Two subgroups H and
![]() $H'$
of G are conjugate, denoted
$H'$
of G are conjugate, denoted
![]() $H\sim H'$
, if there exists
$H\sim H'$
, if there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $H=gH'g^{-1}$
. We let
$H=gH'g^{-1}$
. We let
denote the collection of all conjugation classes of stabilizer subgroups. Set
for
![]() $t\in T$
. We have
$t\in T$
. We have
![]() $\operatorname {\mathrm {Stab}}(g.m)=g\operatorname {\mathrm {Stab}}(m)g^{-1}$
for all
$\operatorname {\mathrm {Stab}}(g.m)=g\operatorname {\mathrm {Stab}}(m)g^{-1}$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $m\in M$
, which implies that each
$m\in M$
, which implies that each
![]() $M_t$
is G-invariant.
$M_t$
is G-invariant.
Let us additionally assume that each
![]() $M_t$
is connected. Then, by [Reference MeinrekenMei03, Theorem 1.30], each
$M_t$
is connected. Then, by [Reference MeinrekenMei03, Theorem 1.30], each
![]() $M_t$
is a smooth embedded submanifold of M, and M decomposes as a disjoint union
$M_t$
is a smooth embedded submanifold of M, and M decomposes as a disjoint union
![]() $M=\bigcup _{t\in T} M_t$
. (See also [Reference BredonBre72, Theorem IV.3.3, p. 182].) Furthermore, this decomposition satisfies the frontier condition: for all
$M=\bigcup _{t\in T} M_t$
. (See also [Reference BredonBre72, Theorem IV.3.3, p. 182].) Furthermore, this decomposition satisfies the frontier condition: for all
![]() $t',t\in T$
, if
$t',t\in T$
, if
![]() $M_{t'}\cap \overline {M_t}\neq \emptyset $
, then
$M_{t'}\cap \overline {M_t}\neq \emptyset $
, then
![]() $M_{t'}\subseteq \overline {M_t}$
. This defines a partial order on T by setting
$M_{t'}\subseteq \overline {M_t}$
. This defines a partial order on T by setting
![]() $t'\leq t$
if
$t'\leq t$
if
![]() $M_{t'}\subseteq \overline {M_t}$
. The depth of
$M_{t'}\subseteq \overline {M_t}$
. The depth of
![]() $t\in T$
is defined as
$t\in T$
is defined as
![]() $\operatorname {\mathrm {depth}}(t)=0$
if t is maximal, and otherwise
$\operatorname {\mathrm {depth}}(t)=0$
if t is maximal, and otherwise
In many cases, one knows that T is finite and contains a largest element (see Sections IV.3 and IV.10 of [Reference BredonBre72]).
Set
![]() $M_{\mathrm {free}}:=\{m\in M : \operatorname {\mathrm {Stab}}(m)=\{1\}\}$
. If
$M_{\mathrm {free}}:=\{m\in M : \operatorname {\mathrm {Stab}}(m)=\{1\}\}$
. If
![]() $M_{\mathrm {free}}\neq \emptyset $
, then the conjugacy class of the trivial subgroup is the largest element in T, and
$M_{\mathrm {free}}\neq \emptyset $
, then the conjugacy class of the trivial subgroup is the largest element in T, and
![]() $M_{\mathrm {free}}$
is an open submanifold of M. The restriction of the action to
$M_{\mathrm {free}}$
is an open submanifold of M. The restriction of the action to
![]() $M_{\mathrm {free}}$
is free.
$M_{\mathrm {free}}$
is free.
Proposition 4.5 Retain the situation from Paragraph 4.4. Assume that M is metrizable with metric
![]() $d_M$
, T is finite, and
$d_M$
, T is finite, and
![]() $M\neq M_{\mathrm {free}}\neq \emptyset $
. Let X be a compact Hausdorff space. Then, the following are equivalent:
$M\neq M_{\mathrm {free}}\neq \emptyset $
. Let X be a compact Hausdorff space. Then, the following are equivalent:
-
(1)
 $C(X,M_{\mathrm {free}})\subseteq C(X,M)$
is dense with respect to the metric
$C(X,M_{\mathrm {free}})\subseteq C(X,M)$
is dense with respect to the metric
 $d(f,g):=\sup _{x\in X}d_M(f(x),g(x))$
, for
$d(f,g):=\sup _{x\in X}d_M(f(x),g(x))$
, for
 $f,g\in C(X,M)$
.
$f,g\in C(X,M)$
. -
(2)
 $\dim (X)<\dim (M)-\dim (M\setminus M_{\mathrm {free}})$
.
$\dim (X)<\dim (M)-\dim (M\setminus M_{\mathrm {free}})$
.
Proof Note that T contains exactly one element of depth zero, namely the conjugacy class of
![]() $\{1\}$
. Therefore,
$\{1\}$
. Therefore,
and it follows that
To show that (1) implies (2), assume that
![]() $\dim (X)\geq \dim (M)-\dim (M\setminus M_{\mathrm {free}})$
. Choose
$\dim (X)\geq \dim (M)-\dim (M\setminus M_{\mathrm {free}})$
. Choose
![]() $t\in T$
of depth
$t\in T$
of depth
![]() $\geq 1$
such that
$\geq 1$
such that
![]() $\dim (X)\geq \dim (M)-\dim (M_t)$
. As noted in [Reference Beggs and EvansBE91, Proposition 1.6], it follows that
$\dim (X)\geq \dim (M)-\dim (M_t)$
. As noted in [Reference Beggs and EvansBE91, Proposition 1.6], it follows that
![]() $C(X,M\setminus M_t)\subseteq C(X,M)$
is not dense, which implies that (1) fails.
$C(X,M\setminus M_t)\subseteq C(X,M)$
is not dense, which implies that (1) fails.
Assuming (2), let us prove (1). Let
![]() $f\in C(X,M)$
and
$f\in C(X,M)$
and
![]() $\varepsilon>0$
. The proof is similar to that of Theorem 1.3 in [Reference Beggs and EvansBE91]. We inductively change f to avoid each
$\varepsilon>0$
. The proof is similar to that of Theorem 1.3 in [Reference Beggs and EvansBE91]. We inductively change f to avoid each
![]() $M_t$
, but instead of proceeding by the (co)dimension of the submanifolds, we use their depths.
$M_t$
, but instead of proceeding by the (co)dimension of the submanifolds, we use their depths.
It follows from the frontier condition that for each
![]() $t\in T$
, the set
$t\in T$
, the set
![]() $\overline {M_t}\setminus M_t$
is contained in the union of submanifolds
$\overline {M_t}\setminus M_t$
is contained in the union of submanifolds
![]() $M_s$
with
$M_s$
with
![]() $s\in T$
and
$s\in T$
and
![]() $\operatorname {\mathrm {depth}}(s)>\operatorname {\mathrm {depth}}(t)$
. Let
$\operatorname {\mathrm {depth}}(s)>\operatorname {\mathrm {depth}}(t)$
. Let
![]() $t_1,\ldots ,t_K$
be an enumeration of the elements in T with depth
$t_1,\ldots ,t_K$
be an enumeration of the elements in T with depth
![]() $\geq 1$
, such that
$\geq 1$
, such that
![]() $\operatorname {\mathrm {depth}}(t_1)\geq \operatorname {\mathrm {depth}}(t_2)\geq \cdots \geq \operatorname {\mathrm {depth}}(t_K)$
. Note that
$\operatorname {\mathrm {depth}}(t_1)\geq \operatorname {\mathrm {depth}}(t_2)\geq \cdots \geq \operatorname {\mathrm {depth}}(t_K)$
. Note that
![]() $M_{t_1}$
is a closed submanifold (since
$M_{t_1}$
is a closed submanifold (since
![]() $t_1$
has maximal depth and thus
$t_1$
has maximal depth and thus
![]() $\overline {M_{t_1}}\setminus M_{t_1}=\emptyset $
), and for each
$\overline {M_{t_1}}\setminus M_{t_1}=\emptyset $
), and for each
![]() $j\geq 2$
, the set
$j\geq 2$
, the set
![]() $\overline {M_{t_j}}\setminus M_{t_j}$
is contained in
$\overline {M_{t_j}}\setminus M_{t_j}$
is contained in
![]() $M_{t_1}\cup \ldots M_{t_{j-1}}$
. Furthermore, every
$M_{t_1}\cup \ldots M_{t_{j-1}}$
. Furthermore, every
![]() $M_{t_j}$
is a submanifold of codimension
$M_{t_j}$
is a submanifold of codimension
![]() $\geq \dim (X)+1$
.
$\geq \dim (X)+1$
.
By [Reference Beggs and EvansBE91, Lemma 1.4], if
![]() $Y\subseteq M$
is submanifold of codimension
$Y\subseteq M$
is submanifold of codimension
![]() $\geq \dim (X)+1$
, if
$\geq \dim (X)+1$
, if
![]() $\delta>0$
, and if
$\delta>0$
, and if
![]() $g\in C(X, M)$
satisfies
$g\in C(X, M)$
satisfies
![]() $g(X)\cap (\overline {Y}\setminus Y)=\emptyset $
, then there exists
$g(X)\cap (\overline {Y}\setminus Y)=\emptyset $
, then there exists
![]() $g'\in C(X,M)$
such that
$g'\in C(X,M)$
such that
![]() $d(g,g')\leq \delta $
and
$d(g,g')\leq \delta $
and
![]() $g'(X)\cap \overline {Y}=\emptyset $
. Set
$g'(X)\cap \overline {Y}=\emptyset $
. Set
![]() $f_0:=f$
. We will inductively find
$f_0:=f$
. We will inductively find
![]() $f_k\in C(X,M)$
such that, for each
$f_k\in C(X,M)$
such that, for each
![]() $k=1,\ldots ,K$
, we have
$k=1,\ldots ,K$
, we have
First, using that the boundary of
![]() $M_{t_1}$
is empty, we can apply [Reference Beggs and EvansBE91, Lemma 1.4] to obtain
$M_{t_1}$
is empty, we can apply [Reference Beggs and EvansBE91, Lemma 1.4] to obtain
![]() $f_1\in C(X,M)$
such that
$f_1\in C(X,M)$
such that
For
![]() $k\geq 2$
, assuming that we have chosen
$k\geq 2$
, assuming that we have chosen
![]() $f_{k-1}$
, let
$f_{k-1}$
, let
![]() $\delta _k$
denote the (positive) distance between the compact set
$\delta _k$
denote the (positive) distance between the compact set
![]() $f_{k-1}(X)$
and
$f_{k-1}(X)$
and
![]() $\overline {M_{t_1}}\cup \cdots \cup \overline {M_{t_{k-1}}}$
. Applying [Reference Beggs and EvansBE91, Lemma 1.4], we obtain
$\overline {M_{t_1}}\cup \cdots \cup \overline {M_{t_{k-1}}}$
. Applying [Reference Beggs and EvansBE91, Lemma 1.4], we obtain
![]() $f_k\in C(X,M)$
such that
$f_k\in C(X,M)$
such that
By choice of
![]() $\delta _k$
, it follows that
$\delta _k$
, it follows that
![]() $f_k(X)$
is disjoint from
$f_k(X)$
is disjoint from
![]() $\overline {M_{t_1}}\cup \cdots \cup \overline {M_{t_k}}$
.
$\overline {M_{t_1}}\cup \cdots \cup \overline {M_{t_k}}$
.
Finally, the element
![]() $f_K$
belongs to
$f_K$
belongs to
![]() $C(X,M_{\mathrm {free}})$
and satisfies
$C(X,M_{\mathrm {free}})$
and satisfies
![]() $d(f,f_K)<\varepsilon $
.
$d(f,f_K)<\varepsilon $
.
4.6. We let
![]() $\operatorname {\mathrm {Sub}}_1(M_d)$
denote the collection of sub-
$\operatorname {\mathrm {Sub}}_1(M_d)$
denote the collection of sub-
![]() $C^*\!$
-algebras of
$C^*\!$
-algebras of
![]() $M_d$
that contain the unit of
$M_d$
that contain the unit of
![]() $M_d$
. Given
$M_d$
. Given
![]() $\mathbf {a}\in E^{n+1}_d:=(M_d)^{n+1}_{\mathrm {sa}}$
, we set
$\mathbf {a}\in E^{n+1}_d:=(M_d)^{n+1}_{\mathrm {sa}}$
, we set
![]() $C^*_1(\mathbf {a}):=C^*(\mathbf {a},1)\in \operatorname {\mathrm {Sub}}_1(M_d)$
. We let
$C^*_1(\mathbf {a}):=C^*(\mathbf {a},1)\in \operatorname {\mathrm {Sub}}_1(M_d)$
. We let
![]() $\mathcal {PU}_d$
act on
$\mathcal {PU}_d$
act on
![]() $\operatorname {\mathrm {Sub}}_1(M_d)$
by
$\operatorname {\mathrm {Sub}}_1(M_d)$
by
![]() $[u].B:=uBu^*$
for
$[u].B:=uBu^*$
for
![]() $u\in {\mathcal {U}}_d$
and
$u\in {\mathcal {U}}_d$
and
![]() $B\in \operatorname {\mathrm {Sub}}_1(M_d)$
. Given
$B\in \operatorname {\mathrm {Sub}}_1(M_d)$
. Given
![]() $B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
, we write
$B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
, we write
![]() $B_1\sim B_2$
if
$B_1\sim B_2$
if
![]() $B_1$
and
$B_1$
and
![]() $B_2$
lie in the same orbit of this action, that is, if
$B_2$
lie in the same orbit of this action, that is, if
![]() $B_1=uB_2u^*$
for some
$B_1=uB_2u^*$
for some
![]() $u\in {\mathcal {U}}_d$
.
$u\in {\mathcal {U}}_d$
.
Given
![]() $\mathbf {a}\in E^{n+1}_d$
, we have
$\mathbf {a}\in E^{n+1}_d$
, we have
![]() $C^*_1(\mathbf {a})=M_d$
if and only if
$C^*_1(\mathbf {a})=M_d$
if and only if
![]() $C^*(\mathbf {a})$
, and thus
$C^*(\mathbf {a})$
, and thus
 $$ \begin{align*} G^{n+1}_d &:= \operatorname{\mathrm{Gen}}_{n+1}(M_d)_{\mathrm{sa}} = \big\{ \mathbf{a}\in (M_d)^{n+1}_{\mathrm{sa}} : C^*(\mathbf{a})=M_d \big\} \\ & \kern2pt= \big\{ \mathbf{a}\in (M_d)^{n+1}_{\mathrm{sa}} : C^*_1(\mathbf{a})=M_d \big\}. \end{align*} $$
$$ \begin{align*} G^{n+1}_d &:= \operatorname{\mathrm{Gen}}_{n+1}(M_d)_{\mathrm{sa}} = \big\{ \mathbf{a}\in (M_d)^{n+1}_{\mathrm{sa}} : C^*(\mathbf{a})=M_d \big\} \\ & \kern2pt= \big\{ \mathbf{a}\in (M_d)^{n+1}_{\mathrm{sa}} : C^*_1(\mathbf{a})=M_d \big\}. \end{align*} $$
Given a sub-
![]() $C^*\!$
-algebra
$C^*\!$
-algebra
![]() $B\subseteq M_d$
, we let
$B\subseteq M_d$
, we let
![]() $B' := \{ c \in M_d : bc=cb \text { for all } b\in B \}$
denote its commutant. We always have
$B' := \{ c \in M_d : bc=cb \text { for all } b\in B \}$
denote its commutant. We always have
![]() $B'\in \operatorname {\mathrm {Sub}}_1(M_d)$
, and by the bicommutant theorem, we have
$B'\in \operatorname {\mathrm {Sub}}_1(M_d)$
, and by the bicommutant theorem, we have
![]() $B"=B$
for all
$B"=B$
for all
![]() $B\in \operatorname {\mathrm {Sub}}_1(M_d)$
.
$B\in \operatorname {\mathrm {Sub}}_1(M_d)$
.
Lemma 4.7 Let
![]() $\mathbf {a}\in E^{n+1}_d$
. Then,
$\mathbf {a}\in E^{n+1}_d$
. Then,
Furthermore, we have
![]() $\mathbf {a}\in G^{n+1}_d$
if and only if
$\mathbf {a}\in G^{n+1}_d$
if and only if
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a})=\{[1]\}$
.
$\operatorname {\mathrm {Stab}}(\mathbf {a})=\{[1]\}$
.
Proof Given
![]() $u\in {\mathcal {U}}_d$
, we have
$u\in {\mathcal {U}}_d$
, we have
![]() $[u].\mathbf {a}=\mathbf {a}$
if and only if
$[u].\mathbf {a}=\mathbf {a}$
if and only if
![]() $uxu^*=x$
for every
$uxu^*=x$
for every
![]() $x\in C^*(\mathbf {a})$
. This implies the formula for
$x\in C^*(\mathbf {a})$
. This implies the formula for
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a})$
.
$\operatorname {\mathrm {Stab}}(\mathbf {a})$
.
If
![]() $\mathbf {a}\in G^{n+1}_d$
, then
$\mathbf {a}\in G^{n+1}_d$
, then
![]() $C^*(\mathbf {a})'=\mathbb {C} 1$
, which implies that
$C^*(\mathbf {a})'=\mathbb {C} 1$
, which implies that
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a})$
is trivial. Conversely, assuming that
$\operatorname {\mathrm {Stab}}(\mathbf {a})$
is trivial. Conversely, assuming that
![]() $\mathbf {a}\in E_d^{n+1}\setminus G_d^{n+1}$
, let us verify that
$\mathbf {a}\in E_d^{n+1}\setminus G_d^{n+1}$
, let us verify that
![]() $\mathbf {a}$
has nontrivial stabilizer subgroup. Since
$\mathbf {a}$
has nontrivial stabilizer subgroup. Since
![]() $C^*(\mathbf {a})\neq M_d$
, we also have
$C^*(\mathbf {a})\neq M_d$
, we also have
![]() $C^*_1(\mathbf {a})\neq M_d$
. Using the bicommutant theorem, we deduce that
$C^*_1(\mathbf {a})\neq M_d$
. Using the bicommutant theorem, we deduce that
![]() $C^*_1(\mathbf {a})'$
is strictly larger than the center of
$C^*_1(\mathbf {a})'$
is strictly larger than the center of
![]() $M_d$
. Using that
$M_d$
. Using that
![]() $C^*(\mathbf {a})'=C^*_1(\mathbf {a})'$
, we obtain a noncentral unitary in
$C^*(\mathbf {a})'=C^*_1(\mathbf {a})'$
, we obtain a noncentral unitary in
![]() $C^*(\mathbf {a})'$
.
$C^*(\mathbf {a})'$
.
Lemma 4.8 Let
![]() $\mathbf {a},\mathbf {b}\in E^{n+1}_d$
. Then, we have
$\mathbf {a},\mathbf {b}\in E^{n+1}_d$
. Then, we have
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
if and only if
$\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
if and only if
![]() $C^*_1(\mathbf {a}) \sim C^*_1(\mathbf {b})$
.
$C^*_1(\mathbf {a}) \sim C^*_1(\mathbf {b})$
.
Proof Let
![]() $B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
. If
$B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
. If
![]() $u\in {\mathcal {U}}_d$
satisfies
$u\in {\mathcal {U}}_d$
satisfies
![]() $uB_1u^*=B_2$
, then one checks
$uB_1u^*=B_2$
, then one checks
![]() $uB_1'u^*=B_2'$
. Using also that
$uB_1'u^*=B_2'$
. Using also that
![]() $B_1$
and
$B_1$
and
![]() $B_2$
agree with their bicommutants, we obtain
$B_2$
agree with their bicommutants, we obtain
Using that
![]() $C^*_1(\mathbf {a}) = C^*(\mathbf {a})"$
and
$C^*_1(\mathbf {a}) = C^*(\mathbf {a})"$
and
![]() $C^*_1(\mathbf {a})' = C^*(\mathbf {a})'$
, and similarly
$C^*_1(\mathbf {a})' = C^*(\mathbf {a})'$
, and similarly
![]() $C^*_1(\mathbf {b}) = C^*(\mathbf {b})"$
and
$C^*_1(\mathbf {b}) = C^*(\mathbf {b})"$
and
![]() $C^*_1(\mathbf {b})' = C^*(\mathbf {b})'$
, we need to show
$C^*_1(\mathbf {b})' = C^*(\mathbf {b})'$
, we need to show
To prove the forward implication, we assume that
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
. Let
$\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
. Let
![]() $v\in {\mathcal {U}}_d$
such that
$v\in {\mathcal {U}}_d$
such that
![]() $[v]\operatorname {\mathrm {Stab}}(\mathbf {a})[v]^{-1}= \operatorname {\mathrm {Stab}}(\mathbf {b})$
. Given
$[v]\operatorname {\mathrm {Stab}}(\mathbf {a})[v]^{-1}= \operatorname {\mathrm {Stab}}(\mathbf {b})$
. Given
![]() $u\in {\mathcal {U}}(C^*(\mathbf {a})')$
, it follows from Lemma 4.7 that
$u\in {\mathcal {U}}(C^*(\mathbf {a})')$
, it follows from Lemma 4.7 that
Using that
![]() $\mathbb {T} 1\subseteq {\mathcal {U}}(C^*(\mathbf {b})')$
, we obtain
$\mathbb {T} 1\subseteq {\mathcal {U}}(C^*(\mathbf {b})')$
, we obtain
![]() $vuv^*\in {\mathcal {U}}(C^*(\mathbf {b})')$
. Since
$vuv^*\in {\mathcal {U}}(C^*(\mathbf {b})')$
. Since
![]() $C^*(\mathbf {a})'$
is spanned by its unitary elements, we get
$C^*(\mathbf {a})'$
is spanned by its unitary elements, we get
![]() $vC^*(\mathbf {a})'v^*\subseteq C^*(\mathbf {b})'$
. The reverse inclusion is shown analogously, whence
$vC^*(\mathbf {a})'v^*\subseteq C^*(\mathbf {b})'$
. The reverse inclusion is shown analogously, whence
![]() $vC^*(\mathbf {a})'v^*= C^*(\mathbf {b})'$
, that is,
$vC^*(\mathbf {a})'v^*= C^*(\mathbf {b})'$
, that is,
![]() $C^*(\mathbf {a})'\sim C^*(\mathbf {b})'$
.
$C^*(\mathbf {a})'\sim C^*(\mathbf {b})'$
.
Conversely, if
![]() $C^*(\mathbf {a})' \sim C^*(\mathbf {b})'$
, let
$C^*(\mathbf {a})' \sim C^*(\mathbf {b})'$
, let
![]() $v\in {\mathcal {U}}_d$
such that
$v\in {\mathcal {U}}_d$
such that
![]() $uC^*(\mathbf {a})'v^*=C^*(\mathbf {b})'$
. Using Lemma 4.7, we get
$uC^*(\mathbf {a})'v^*=C^*(\mathbf {b})'$
. Using Lemma 4.7, we get
![]() $[v]\operatorname {\mathrm {Stab}}(\mathbf {a})[v]^{-1}= \operatorname {\mathrm {Stab}}(\mathbf {b})$
, that is,
$[v]\operatorname {\mathrm {Stab}}(\mathbf {a})[v]^{-1}= \operatorname {\mathrm {Stab}}(\mathbf {b})$
, that is,
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
.
$\operatorname {\mathrm {Stab}}(\mathbf {a}) \sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
.
Lemma 4.9 Let B be a finite-dimensional
![]() $C^*\!$
-algebra and
$C^*\!$
-algebra and
![]() $n\geq 1$
. Then, the set
$n\geq 1$
. Then, the set
![]() $\{\mathbf {a}\in B^{n+1}_{\mathrm {sa}} : C^*_1(\mathbf {a})=B\}$
is a path-connected, dense, open subset of
$\{\mathbf {a}\in B^{n+1}_{\mathrm {sa}} : C^*_1(\mathbf {a})=B\}$
is a path-connected, dense, open subset of
![]() $B^{n+1}_{\mathrm {sa}}$
.
$B^{n+1}_{\mathrm {sa}}$
.
Proof Set
![]() $G:=\{\mathbf {a}\in B^{n+1}_{\mathrm {sa}} : C^*_1(\mathbf {a})=B\}$
.
$G:=\{\mathbf {a}\in B^{n+1}_{\mathrm {sa}} : C^*_1(\mathbf {a})=B\}$
.
Denseness: By [Reference Thiel and WinterThi21, Lemma 7.2], we have
![]() $\operatorname {\mathrm {gr}}(B)\leq 1\leq n$
. Since B is unital and separable, it follows from Theorem 2.2 that
$\operatorname {\mathrm {gr}}(B)\leq 1\leq n$
. Since B is unital and separable, it follows from Theorem 2.2 that
![]() $\operatorname {\mathrm {Gen}}_{n+1}(B)_{\mathrm {sa}}\subseteq B^{n+1}_{\mathrm {sa}}$
is dense. Using that
$\operatorname {\mathrm {Gen}}_{n+1}(B)_{\mathrm {sa}}\subseteq B^{n+1}_{\mathrm {sa}}$
is dense. Using that
![]() $\operatorname {\mathrm {Gen}}_{n+1}(B)_{\mathrm {sa}}\subseteq G$
, we get that G is also dense in
$\operatorname {\mathrm {Gen}}_{n+1}(B)_{\mathrm {sa}}\subseteq G$
, we get that G is also dense in
![]() $B^{n+1}_{\mathrm {sa}}$
.
$B^{n+1}_{\mathrm {sa}}$
.
Openness: Let
![]() $\mathcal {D}$
denote the family of sub-
$\mathcal {D}$
denote the family of sub-
![]() $C^*\!$
-algebras
$C^*\!$
-algebras
![]() $D\subseteq B$
such that
$D\subseteq B$
such that
![]() $D+\mathbb {C} 1_B$
is a proper sub-
$D+\mathbb {C} 1_B$
is a proper sub-
![]() $C^*\!$
-algebra of B (that is,
$C^*\!$
-algebra of B (that is,
![]() $C^*_1(D)\neq B$
). Then,
$C^*_1(D)\neq B$
). Then,
Thus, we need to show that
![]() $\bigcup _{D\in \mathcal {D}} D^{n+1}_{\mathrm {sa}}$
is a closed subset of
$\bigcup _{D\in \mathcal {D}} D^{n+1}_{\mathrm {sa}}$
is a closed subset of
![]() $B^{n+1}_{\mathrm {sa}}$
.
$B^{n+1}_{\mathrm {sa}}$
.
We let
![]() ${\mathcal {U}}(B)$
denote the unitary group of B. It naturally acts on
${\mathcal {U}}(B)$
denote the unitary group of B. It naturally acts on
![]() $\mathcal {D}$
by setting
$\mathcal {D}$
by setting
![]() $u.D:=uDu^*$
for
$u.D:=uDu^*$
for
![]() $u\in {\mathcal {U}}(B)$
and
$u\in {\mathcal {U}}(B)$
and
![]() $D\in \mathcal {D}$
. Since B is finite-dimensional, two sub-
$D\in \mathcal {D}$
. Since B is finite-dimensional, two sub-
![]() $C^*\!$
-algebras
$C^*\!$
-algebras
![]() $D_1,D_2\subseteq B$
are unitarily equivalent if and only if
$D_1,D_2\subseteq B$
are unitarily equivalent if and only if
![]() $D_1\cong D_2$
and the inclusions induce the same maps in ordered
$D_1\cong D_2$
and the inclusions induce the same maps in ordered
![]() $K_0$
-theory. It follows that the action
$K_0$
-theory. It follows that the action
![]() ${\mathcal {U}}(B)\curvearrowright \mathcal {D}$
has only finitely many orbits, and we choose representatives
${\mathcal {U}}(B)\curvearrowright \mathcal {D}$
has only finitely many orbits, and we choose representatives
![]() $D_1,\ldots ,D_m\in \mathcal {D}$
. Then,
$D_1,\ldots ,D_m\in \mathcal {D}$
. Then,
![]() $\mathcal {D}=\bigcup _{j=1}^m \bigcup _{u\in {\mathcal {U}}{B}} uD_ju^*$
.
$\mathcal {D}=\bigcup _{j=1}^m \bigcup _{u\in {\mathcal {U}}{B}} uD_ju^*$
.
For each j, since
![]() $D_j$
is a closed subset of B, it follows that
$D_j$
is a closed subset of B, it follows that
![]() $(D_j)^{n+1}_{\mathrm {sa}}$
is a closed subset of
$(D_j)^{n+1}_{\mathrm {sa}}$
is a closed subset of
![]() $B^{n+1}_{\mathrm {sa}}$
. Since B is finite-dimensional,
$B^{n+1}_{\mathrm {sa}}$
. Since B is finite-dimensional,
![]() ${\mathcal {U}}(B)$
is compact, and it follows that
${\mathcal {U}}(B)$
is compact, and it follows that
 $$\begin{align*}\bigcup_{D\in\mathcal{D}} D^{n+1}_{\mathrm{sa}} = \bigcup_{j=1}^m \bigcup_{u\in{\mathcal{U}}(B)} u(D_j)^{n+1}_{\mathrm{sa}} u^* \end{align*}$$
$$\begin{align*}\bigcup_{D\in\mathcal{D}} D^{n+1}_{\mathrm{sa}} = \bigcup_{j=1}^m \bigcup_{u\in{\mathcal{U}}(B)} u(D_j)^{n+1}_{\mathrm{sa}} u^* \end{align*}$$
is closed, as desired.
Path-connectedness: We only sketch the argument for the case
![]() $B=M_d$
for some
$B=M_d$
for some
![]() $d\,{\geq}\, 2$
. Let
$d\,{\geq}\, 2$
. Let
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
. Using that the unitary group of
$\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
. Using that the unitary group of
![]() $M_d$
is path-connected, and that
$M_d$
is path-connected, and that
![]() $a_0$
is unitarily equivalent to a diagonal matrix, we find a path in
$a_0$
is unitarily equivalent to a diagonal matrix, we find a path in
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
from
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
from
![]() $\mathbf {a}$
to some
$\mathbf {a}$
to some
![]() $\mathbf {b}$
such that
$\mathbf {b}$
such that
![]() $b_0$
is diagonal. By splitting multiple eigenvalues of
$b_0$
is diagonal. By splitting multiple eigenvalues of
![]() $b_0$
and moving them away from zero, we find a path
$b_0$
and moving them away from zero, we find a path
![]() $(x_t)_{t\in [0,1]}$
inside the self-adjoint, diagonal matrices starting with
$(x_t)_{t\in [0,1]}$
inside the self-adjoint, diagonal matrices starting with
![]() $x_0=b_0$
and ending with some
$x_0=b_0$
and ending with some
![]() $x_1$
such that
$x_1$
such that
![]() $x_1$
has k distinct, nonzero diagonal entries, and such that
$x_1$
has k distinct, nonzero diagonal entries, and such that
![]() $b_0\in C^*(x_t)$
for each
$b_0\in C^*(x_t)$
for each
![]() $t\in [0,1]$
. Then,
$t\in [0,1]$
. Then,
![]() $t\mapsto (x_t,b_1,\ldots ,b_n)$
defines a path inside
$t\mapsto (x_t,b_1,\ldots ,b_n)$
defines a path inside
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
.
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
.
Let S denote the set of self-adjoint matrices in
![]() $M_d$
such that every off-diagonal entry is nonzero. Note that S is path-connected. Next, we let
$M_d$
such that every off-diagonal entry is nonzero. Note that S is path-connected. Next, we let
![]() $(y_t)_{t\in [0,1]}$
be a path inside the self-adjoint matrices starting with
$(y_t)_{t\in [0,1]}$
be a path inside the self-adjoint matrices starting with
![]() $y_0=b_1$
, ending with some matrix
$y_0=b_1$
, ending with some matrix
![]() $y_1$
that has the eigenvalues
$y_1$
that has the eigenvalues
![]() $1,2,\ldots ,d$
such that
$1,2,\ldots ,d$
such that
![]() $y_t$
belongs to S for every
$y_t$
belongs to S for every
![]() $t\in (0,1]$
. Note that
$t\in (0,1]$
. Note that
![]() $x_1$
and
$x_1$
and
![]() $y_t$
generated
$y_t$
generated
![]() $M_d$
for every
$M_d$
for every
![]() $t\in (0,1]$
. It follows that
$t\in (0,1]$
. It follows that
![]() $t\mapsto (x_1,y_t,b_2,\ldots ,b_n)$
defines a path inside
$t\mapsto (x_1,y_t,b_2,\ldots ,b_n)$
defines a path inside
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
.
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
.
Conjugating by a suitable path of unitaries, we find a path in
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
from
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
from
![]() $(x_1,y_1,b_2,\ldots ,b_n)$
to some
$(x_1,y_1,b_2,\ldots ,b_n)$
to some
![]() $\mathbf {c}=(c_0,c_1,\ldots ,c_n)$
such that
$\mathbf {c}=(c_0,c_1,\ldots ,c_n)$
such that
![]() $c_1=\operatorname {\mathrm {diag}}(1,2,\ldots ,d)$
. Arguing as above, we find a path in
$c_1=\operatorname {\mathrm {diag}}(1,2,\ldots ,d)$
. Arguing as above, we find a path in
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
that changes
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
that changes
![]() $c_0$
to the matrix
$c_0$
to the matrix
![]() $\tilde {c_0}$
with all entries
$\tilde {c_0}$
with all entries
![]() $1$
. Then,
$1$
. Then,
![]() $\tilde {c_0}$
and
$\tilde {c_0}$
and
![]() $c_1$
generate
$c_1$
generate
![]() $M_d$
.
$M_d$
.
Then,
![]() $t\mapsto (\tilde {c_0},c_1,(1-t)c_2,\ldots ,(1-t)c_n)$
is a path in
$t\mapsto (\tilde {c_0},c_1,(1-t)c_2,\ldots ,(1-t)c_n)$
is a path in
![]() $\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
connecting to
$\operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
connecting to
![]() $(\tilde {c_0},c_1,0\ldots ,0)$
. Thus, every
$(\tilde {c_0},c_1,0\ldots ,0)$
. Thus, every
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
is path-connected to the same element.
$\mathbf {a}\in \operatorname {\mathrm {Gen}}_{n+1}(M_d)_{\mathrm {sa}}$
is path-connected to the same element.
4.10. Let
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $n\in \mathbb {N}$
. The compact Lie group
$n\in \mathbb {N}$
. The compact Lie group
![]() $\mathcal {PU}_d$
acts smoothly on the manifold
$\mathcal {PU}_d$
acts smoothly on the manifold
![]() $E^{n+1}_d:=(M_d)^{n+1}_{\mathrm {sa}}$
. We will describe the corresponding orbit-type decomposition of
$E^{n+1}_d:=(M_d)^{n+1}_{\mathrm {sa}}$
. We will describe the corresponding orbit-type decomposition of
![]() $E^{n+1}_d$
.
$E^{n+1}_d$
.
Given
![]() $\mathbf {a},\mathbf {b}\in E^{n+1}_d$
, by Lemma 4.8, we have
$\mathbf {a},\mathbf {b}\in E^{n+1}_d$
, by Lemma 4.8, we have
![]() $\operatorname {\mathrm {Stab}}(\mathbf {a})\sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
if and only if
$\operatorname {\mathrm {Stab}}(\mathbf {a})\sim \operatorname {\mathrm {Stab}}(\mathbf {b})$
if and only if
![]() $C^*_1(\mathbf {a})\sim C^*_1(\mathbf {b})$
. Moreover, given
$C^*_1(\mathbf {a})\sim C^*_1(\mathbf {b})$
. Moreover, given
![]() $B\in \operatorname {\mathrm {Sub}}_1(M_d)$
, there exists
$B\in \operatorname {\mathrm {Sub}}_1(M_d)$
, there exists
![]() $\mathbf {a}\in E^{n+1}_d$
with
$\mathbf {a}\in E^{n+1}_d$
with
![]() $B=C^*_1(\mathbf {a})$
. It follows that the orbit types of
$B=C^*_1(\mathbf {a})$
. It follows that the orbit types of
![]() $\mathcal {PU}_d\curvearrowright E^{n+1}_d$
naturally correspond to the orbit types of the action
$\mathcal {PU}_d\curvearrowright E^{n+1}_d$
naturally correspond to the orbit types of the action
![]() $\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
.
$\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
.
Given
![]() $B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
, it is well known that
$B_1,B_2\in \operatorname {\mathrm {Sub}}_1(M_d)$
, it is well known that
![]() $B_1\sim B_2$
if and only if
$B_1\sim B_2$
if and only if
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are isomorphic, that is,
$B_2$
are isomorphic, that is,
![]() $B_1\cong B_2\cong \oplus _{j=1}^L M_{d_j}$
for some
$B_1\cong B_2\cong \oplus _{j=1}^L M_{d_j}$
for some
![]() $L,d_1,\ldots ,d_L\geq 1$
, and if, for each j, the maps
$L,d_1,\ldots ,d_L\geq 1$
, and if, for each j, the maps
![]() $M_{d_j}\to B_1\to M_d$
and
$M_{d_j}\to B_1\to M_d$
and
![]() $M_{d_j}\to B_2\to M_d$
have the same multiplicity
$M_{d_j}\to B_2\to M_d$
have the same multiplicity
![]() $m_j$
. Thus, to parametrize the orbit types of
$m_j$
. Thus, to parametrize the orbit types of
![]() $\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
, we consider
$\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
, we consider
 $$\begin{align*}T_0 := \left\{ \big( (d_1,\ldots,d_L),(m_1,\ldots,m_L) \big) : L,d_j,m_j\geq 1, \sum_{j=1}^L d_jm_j=d \right\}. \end{align*}$$
$$\begin{align*}T_0 := \left\{ \big( (d_1,\ldots,d_L),(m_1,\ldots,m_L) \big) : L,d_j,m_j\geq 1, \sum_{j=1}^L d_jm_j=d \right\}. \end{align*}$$
Given
![]() $(\mathbf {d},\mathbf {m})\in T_0$
, we let
$(\mathbf {d},\mathbf {m})\in T_0$
, we let
![]() $B(\mathbf {d},\mathbf {m})\subseteq M_d$
be the sub-
$B(\mathbf {d},\mathbf {m})\subseteq M_d$
be the sub-
![]() $C^*\!$
-algebra of block diagonal matrices, with
$C^*\!$
-algebra of block diagonal matrices, with
![]() $m_1$
equal blocks of size
$m_1$
equal blocks of size
![]() $d_1$
, followed by
$d_1$
, followed by
![]() $m_2$
equal blocks of size
$m_2$
equal blocks of size
![]() $d_2$
, and so on. We point out that the numbers
$d_2$
, and so on. We point out that the numbers
![]() $d_1,\ldots ,d_L$
are not required to be distinct. For example,
$d_1,\ldots ,d_L$
are not required to be distinct. For example,
![]() $B((d),(1))=M_d$
,
$B((d),(1))=M_d$
,
![]() $B((1),(d))=\mathbb {C} 1$
, and
$B((1),(d))=\mathbb {C} 1$
, and
![]() $B((1,\ldots ,1),(1,\ldots ,1))$
is the algebra of diagonal matrices.
$B((1,\ldots ,1),(1,\ldots ,1))$
is the algebra of diagonal matrices.
We define an equivalence relation on
![]() $T_0$
by setting
$T_0$
by setting
![]() $(\mathbf {d},\mathbf {m})\sim (\mathbf {d}',\mathbf {m}')$
if all tuples
$(\mathbf {d},\mathbf {m})\sim (\mathbf {d}',\mathbf {m}')$
if all tuples
![]() $\mathbf {d},\mathbf {m},\mathbf {d}',\mathbf {m}'$
contain the same number of elements, say
$\mathbf {d},\mathbf {m},\mathbf {d}',\mathbf {m}'$
contain the same number of elements, say
![]() $L\geq 1$
, and if there is a permutation
$L\geq 1$
, and if there is a permutation
![]() $\sigma $
of
$\sigma $
of
![]() $\{1,\ldots ,L\}$
such that
$\{1,\ldots ,L\}$
such that
For example, we have
![]() $((2,2),(1,2))\sim ((2,2),(2,1))$
, but
$((2,2),(1,2))\sim ((2,2),(2,1))$
, but
![]() $((2,2),(1,2))\nsim ((2),(3))$
.
$((2,2),(1,2))\nsim ((2),(3))$
.
We have
![]() $(\mathbf {d},\mathbf {m})\sim (\mathbf {d}',\mathbf {m}')$
if and only if
$(\mathbf {d},\mathbf {m})\sim (\mathbf {d}',\mathbf {m}')$
if and only if
![]() $B(\mathbf {d},\mathbf {m})\sim B(\mathbf {d}',\mathbf {m}')$
.
$B(\mathbf {d},\mathbf {m})\sim B(\mathbf {d}',\mathbf {m}')$
.
Set
![]() $T:=T_0/_\sim $
. Given
$T:=T_0/_\sim $
. Given
![]() $(\mathbf {d},\mathbf {m})\in T_0$
, we let
$(\mathbf {d},\mathbf {m})\in T_0$
, we let
![]() $[\mathbf {d},\mathbf {m}]$
denote its equivalence class in T. For every
$[\mathbf {d},\mathbf {m}]$
denote its equivalence class in T. For every
![]() $B\in \operatorname {\mathrm {Sub}}_1(M_d)$
, there exists
$B\in \operatorname {\mathrm {Sub}}_1(M_d)$
, there exists
![]() $(\mathbf {d},\mathbf {m})\in T_0$
such that
$(\mathbf {d},\mathbf {m})\in T_0$
such that
![]() $B\sim B(\mathbf {d},\mathbf {m})$
. It follows that the orbit types of
$B\sim B(\mathbf {d},\mathbf {m})$
. It follows that the orbit types of
![]() $\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
are parametrized by T:
$\mathcal {PU}_d\curvearrowright \operatorname {\mathrm {Sub}}_1(M_d)$
are parametrized by T:
Given
![]() $[\mathbf {d},\mathbf {m}]\in T$
, set
$[\mathbf {d},\mathbf {m}]\in T$
, set
Then,
![]() $E_{[\mathbf {d},\mathbf {m}]}$
is the submanifold of
$E_{[\mathbf {d},\mathbf {m}]}$
is the submanifold of
![]() $E^{n+1}_d$
corresponding to orbit type
$E^{n+1}_d$
corresponding to orbit type
![]() $[\mathbf {d},\mathbf {m}]$
, and the orbit-type decomposition (as described in Paragraph 4.4) for
$[\mathbf {d},\mathbf {m}]$
, and the orbit-type decomposition (as described in Paragraph 4.4) for
![]() $\mathcal {PU}_d\curvearrowright E^{n+1}_d$
is
$\mathcal {PU}_d\curvearrowright E^{n+1}_d$
is
By Lemma 4.7, a tuple
![]() $\mathbf {a}\in E^{n+1}_d$
has trivial stabilizer group if and only if
$\mathbf {a}\in E^{n+1}_d$
has trivial stabilizer group if and only if
![]() $\mathbf {a}$
belongs to
$\mathbf {a}$
belongs to
![]() $G^{n+1}_d$
. It follows that
$G^{n+1}_d$
. It follows that
![]() $G^{n+1}_d = E_{[(d),(1)]}$
, and in the notation of Paragraph 4.4, with
$G^{n+1}_d = E_{[(d),(1)]}$
, and in the notation of Paragraph 4.4, with
![]() $M=E^{n+1}_d$
, we have
$M=E^{n+1}_d$
, we have
![]() $M_{\mathrm {free}}=G^{n+1}_d$
.
$M_{\mathrm {free}}=G^{n+1}_d$
.
Lemma 4.11 Let
![]() $[\mathbf {d},\mathbf {m}]\in T$
with
$[\mathbf {d},\mathbf {m}]\in T$
with
![]() $[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
. Then,
$[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
. Then,
![]() $E_{[\mathbf {d},\mathbf {m}]}$
is a connected submanifold of
$E_{[\mathbf {d},\mathbf {m}]}$
is a connected submanifold of
![]() $E^{n+1}_d$
satisfying
$E^{n+1}_d$
satisfying
Furthermore,
![]() $\dim ( E_{[(d-1,1),(1,1)]} ) = (n+1)d^2 -2n(d-1)$
.
$\dim ( E_{[(d-1,1),(1,1)]} ) = (n+1)d^2 -2n(d-1)$
.
Proof Set
![]() $B:=B(\mathbf {d},\mathbf {m})$
. Note that a tuple
$B:=B(\mathbf {d},\mathbf {m})$
. Note that a tuple
![]() $\mathbf {a}\in E^{n+1}_d$
belongs to
$\mathbf {a}\in E^{n+1}_d$
belongs to
![]() $E_{[\mathbf {d},\mathbf {m}]}$
if and only if
$E_{[\mathbf {d},\mathbf {m}]}$
if and only if
![]() $C^*_1(\mathbf {a})\sim B$
. Set
$C^*_1(\mathbf {a})\sim B$
. Set
By Lemma 4.9, F is connected. Since every orbit in
![]() $E_{[\mathbf {d},\mathbf {m}]}$
meets F, and since
$E_{[\mathbf {d},\mathbf {m}]}$
meets F, and since
![]() $\mathcal {PU}_d$
is connected, it follows that
$\mathcal {PU}_d$
is connected, it follows that
![]() $E_{[\mathbf {d},\mathbf {m}]}$
is connected as well.
$E_{[\mathbf {d},\mathbf {m}]}$
is connected as well.
By [Reference BredonBre72, Theorem IV.3.8], if a compact Lie group L acts smoothly on a connected manifold M such that all orbits have the same type, then
![]() $\dim (M)=\dim (M/L)+\dim (L/K)$
, where K is the stabilizer subgroup of any element in M.
$\dim (M)=\dim (M/L)+\dim (L/K)$
, where K is the stabilizer subgroup of any element in M.
Let
![]() $K\subseteq \mathcal {PU}_d$
be the stabilizer subgroup of some element in F. By considering the restricted action
$K\subseteq \mathcal {PU}_d$
be the stabilizer subgroup of some element in F. By considering the restricted action
![]() $\mathcal {PU}_d\curvearrowright E_{[\mathbf {d},\mathbf {m}]}$
, we obtain that
$\mathcal {PU}_d\curvearrowright E_{[\mathbf {d},\mathbf {m}]}$
, we obtain that
Closed subgroups of Lie groups are again Lie groups. It follows that K is a Lie group as well. Since K is acting freely on the connected manifold
![]() $\mathcal {PU}_d$
with only one orbit type, we also get
$\mathcal {PU}_d$
with only one orbit type, we also get
![]() $\dim ( \mathcal {PU}_d/ K ) = \dim ( \mathcal {PU}_d ) - \dim (K)$
and thus
$\dim ( \mathcal {PU}_d/ K ) = \dim ( \mathcal {PU}_d ) - \dim (K)$
and thus
Set
which is a closed subgroup of
![]() $\mathcal {PU}_d$
. Given
$\mathcal {PU}_d$
. Given
![]() $\mathbf {a}\in F$
and
$\mathbf {a}\in F$
and
![]() $[u]\in \mathcal {PU}_d$
, we have
$[u]\in \mathcal {PU}_d$
, we have
![]() $[u].\mathbf {a}\in F$
if and only if
$[u].\mathbf {a}\in F$
if and only if
![]() $[u]\in N$
. It follows that N naturally acts on F. Furthermore, for each
$[u]\in N$
. It follows that N naturally acts on F. Furthermore, for each
![]() $\mathbf {a}\in F$
, the N-orbit
$\mathbf {a}\in F$
, the N-orbit
![]() $N.\mathbf {a}$
agrees with
$N.\mathbf {a}$
agrees with
![]() $\mathcal {PU}_d.\mathbf {a}\cap F$
. Since every
$\mathcal {PU}_d.\mathbf {a}\cap F$
. Since every
![]() $\mathcal {PU}_d$
-orbit in
$\mathcal {PU}_d$
-orbit in
![]() $E_{[\mathbf {d},\mathbf {m}]}$
meets F, we deduce that
$E_{[\mathbf {d},\mathbf {m}]}$
meets F, we deduce that
![]() $E_{[\mathbf {d},\mathbf {m}]} / \mathcal {PU}_d \cong F / N$
. Note that
$E_{[\mathbf {d},\mathbf {m}]} / \mathcal {PU}_d \cong F / N$
. Note that
![]() $B^{n+1}_{\mathrm {sa}}$
is a linear space. By Lemma 4.9, F is an open subset of
$B^{n+1}_{\mathrm {sa}}$
is a linear space. By Lemma 4.9, F is an open subset of
![]() $B^{n+1}_{\mathrm {sa}}$
. It follows that F is a manifold satisfying
$B^{n+1}_{\mathrm {sa}}$
. It follows that F is a manifold satisfying
 $$\begin{align*}\dim(F) = \dim(B^{n+1}_{\mathrm{sa}}) = (n+1)\sum_{j=1}^L d_j^2. \end{align*}$$
$$\begin{align*}\dim(F) = \dim(B^{n+1}_{\mathrm{sa}}) = (n+1)\sum_{j=1}^L d_j^2. \end{align*}$$
Analogous to (4.1), by considering the action of the compact Lie group N on F, we obtain
Note that N contains
![]() $\{[u]:u\in {\mathcal {U}}(B)\}$
, which implies that
$\{[u]:u\in {\mathcal {U}}(B)\}$
, which implies that
 $$\begin{align*}\dim(N)\geq \left(\sum_{j=1}^L d_j^2 \right) - 1. \end{align*}$$
$$\begin{align*}\dim(N)\geq \left(\sum_{j=1}^L d_j^2 \right) - 1. \end{align*}$$
Combining this estimate with (4.1) and (4.2), using that
![]() $E_{[\mathbf {d},\mathbf {m}]} / \mathcal {PU}_d \cong F / N$
, and that
$E_{[\mathbf {d},\mathbf {m}]} / \mathcal {PU}_d \cong F / N$
, and that
![]() $[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
, we get
$[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
, we get
 $$ \begin{align*} \dim( E_{[\mathbf{d},\mathbf{m}]} ) &= \dim( F ) + \dim( \mathcal{PU}_d ) - \dim( N ) \\ &\leq \left( (n+1)\sum_{j=1}^L d_j^2 \right) + \left( d^2 - 1 \right) - \left( \left(\sum_{j=1}^L d_j^2\right) -1 \right) \\ &= d^2 + n\sum_{j=1}^L d_j^2 \\ &\leq d^2 + n((d-1)^2+1) = (n+1)d^2 -2n(d-1). \end{align*} $$
$$ \begin{align*} \dim( E_{[\mathbf{d},\mathbf{m}]} ) &= \dim( F ) + \dim( \mathcal{PU}_d ) - \dim( N ) \\ &\leq \left( (n+1)\sum_{j=1}^L d_j^2 \right) + \left( d^2 - 1 \right) - \left( \left(\sum_{j=1}^L d_j^2\right) -1 \right) \\ &= d^2 + n\sum_{j=1}^L d_j^2 \\ &\leq d^2 + n((d-1)^2+1) = (n+1)d^2 -2n(d-1). \end{align*} $$
For
![]() $[\mathbf {d},\mathbf {m}]=[(d-1,1),(1,1)]$
, we have
$[\mathbf {d},\mathbf {m}]=[(d-1,1),(1,1)]$
, we have
![]() $B(\mathbf {d},\mathbf {m})\cong M_{d-1}\oplus \mathbb {C}\subseteq M_d$
. In this case, we get
$B(\mathbf {d},\mathbf {m})\cong M_{d-1}\oplus \mathbb {C}\subseteq M_d$
. In this case, we get
![]() $N=\{[u]\in \mathcal {PU}_d: u\in {\mathcal {U}}(M_{d-1}\oplus \mathbb {C})\}$
and thus
$N=\{[u]\in \mathcal {PU}_d: u\in {\mathcal {U}}(M_{d-1}\oplus \mathbb {C})\}$
and thus
![]() $\dim (N)=(d-1)^2+1-1= (d-1)^2$
. It follows that
$\dim (N)=(d-1)^2+1-1= (d-1)^2$
. It follows that
 $$ \begin{align*} \dim( E_{[(d-1,1),(1,1)]} ) &= \dim( F ) + \dim( \mathcal{PU}_d ) - \dim( N ) \\ &= (n+1)((d-1)^2+1) + (d^2-1) - (d-1)^2 \\ &= (n+1)d^2 -2n(d-1). \\[-34pt] \end{align*} $$
$$ \begin{align*} \dim( E_{[(d-1,1),(1,1)]} ) &= \dim( F ) + \dim( \mathcal{PU}_d ) - \dim( N ) \\ &= (n+1)((d-1)^2+1) + (d^2-1) - (d-1)^2 \\ &= (n+1)d^2 -2n(d-1). \\[-34pt] \end{align*} $$
Lemma 4.12 Let X be a compact Hausdorff space,
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $n\in \mathbb {N}$
. Then, the following are equivalent:
$n\in \mathbb {N}$
. Then, the following are equivalent:
-
(1)
 $C(X,G^{n+1}_d)\subseteq C(X,E^{n+1}_d)$
is dense.
$C(X,G^{n+1}_d)\subseteq C(X,E^{n+1}_d)$
is dense. -
(2)
 $\dim (X) < 2n(d-1)$
.
$\dim (X) < 2n(d-1)$
.
Proof We use the notation from Paragraph 4.10. The orbit-type decomposition for the action
![]() $\mathcal {PU}_d\curvearrowright E^{n+1}_d$
is
$\mathcal {PU}_d\curvearrowright E^{n+1}_d$
is
Furthermore,
![]() $G^{n+1}_d = E_{[(d),(1)]}$
, which is the submanifold of orbits with trivial stabilizers. In the notation of Paragraph 4.4, with
$G^{n+1}_d = E_{[(d),(1)]}$
, which is the submanifold of orbits with trivial stabilizers. In the notation of Paragraph 4.4, with
![]() $M=E^{n+1}_d$
, we have
$M=E^{n+1}_d$
, we have
![]() $M_{\mathrm {free}}=G^{n+1}_d$
.
$M_{\mathrm {free}}=G^{n+1}_d$
.
Applying Proposition 4.5, we obtain that
![]() $C(X,G^{n+1}_d)\subseteq C(X,E^{n+1}_d)$
is dense if and only if
$C(X,G^{n+1}_d)\subseteq C(X,E^{n+1}_d)$
is dense if and only if
Since
![]() $E^{n+1}_d\setminus G^{n+1}_d$
is the finite union of
$E^{n+1}_d\setminus G^{n+1}_d$
is the finite union of
![]() $E_{[\mathbf {d},\mathbf {m}]}$
for
$E_{[\mathbf {d},\mathbf {m}]}$
for
![]() $[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
, we obtain from Lemma 4.11
$[\mathbf {d},\mathbf {m}]\neq [(d),(1)]$
, we obtain from Lemma 4.11
Now, the result follows using that
![]() $\dim (E^{n+1}_d)=(n+1)d^2$
.
$\dim (E^{n+1}_d)=(n+1)d^2$
.
The next result provides the answer to question (a) from Paragraph 4.3. Recall that
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
denotes the set of tuples that are fiberwise generators.
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
denotes the set of tuples that are fiberwise generators.
Lemma 4.13 Let A be a unital, separable, d-homogeneous
![]() $C^*\!$
-algebra,
$C^*\!$
-algebra,
![]() $d\geq 2$
, and
$d\geq 2$
, and
![]() $n\,{\in}\, \mathbb {N}$
. Then,
$n\,{\in}\, \mathbb {N}$
. Then,
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is open. Furthermore, the following are equivalent:
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is open. Furthermore, the following are equivalent:
-
(1)
 $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
is dense in
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
is dense in
 $A^{n+1}_{\mathrm {sa}}$
.
$A^{n+1}_{\mathrm {sa}}$
. -
(2)
 $\dim (\operatorname {\mathrm {Prim}}(A)) < 2n(d-1)$
.
$\dim (\operatorname {\mathrm {Prim}}(A)) < 2n(d-1)$
.
Proof Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. Since X is compact, and since the
$X:=\operatorname {\mathrm {Prim}}(A)$
. Since X is compact, and since the
![]() $M_d$
-bundle associated with A is locally trivial, we can choose closed subsets
$M_d$
-bundle associated with A is locally trivial, we can choose closed subsets
![]() $X_1,\ldots ,X_m\subseteq X$
that cover X such that
$X_1,\ldots ,X_m\subseteq X$
that cover X such that
![]() $A(X_j)\cong C(X_j,M_d)$
for each j. Let
$A(X_j)\cong C(X_j,M_d)$
for each j. Let
![]() $\pi _j\colon A\to C(X_j,M_d)$
be the corresponding quotient map, which induces a natural map
$\pi _j\colon A\to C(X_j,M_d)$
be the corresponding quotient map, which induces a natural map
![]() $A^{n+1}_{\mathrm {sa}}\to C(X_j,M_d)^{n+1}_{\mathrm {sa}} \cong C(X_j,E^{n+1}_d)$
that we also denote by
$A^{n+1}_{\mathrm {sa}}\to C(X_j,M_d)^{n+1}_{\mathrm {sa}} \cong C(X_j,E^{n+1}_d)$
that we also denote by
![]() $\pi _j$
.
$\pi _j$
.
A tuple
![]() $\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
belongs to
$\mathbf {a}\in A^{n+1}_{\mathrm {sa}}$
belongs to
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
if and only if
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
if and only if
![]() $\pi _j(\mathbf {a})$
belongs to
$\pi _j(\mathbf {a})$
belongs to
![]() $C(X_j,G^{n+1}_d)$
for each j. It follows from Lemma 4.9 that
$C(X_j,G^{n+1}_d)$
for each j. It follows from Lemma 4.9 that
![]() $G^{n+1}_d\subseteq E^{n+1}_d$
is open. Since X is compact, we obtain that
$G^{n+1}_d\subseteq E^{n+1}_d$
is open. Since X is compact, we obtain that
![]() $C(X_j,G^{n+1}_d)\subseteq C(X_j,E^{n+1}_d)$
is always open. Hence,
$C(X_j,G^{n+1}_d)\subseteq C(X_j,E^{n+1}_d)$
is always open. Hence,
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is open.
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is open.
Since the intersection of finitely many open dense sets is again dense, we see that (1) holds if and only if
![]() $C(X_j,G^{n+1}_d)\subseteq C(X_j,E^{n+1}_d)$
is dense for each j. By Lemma 4.12, this is in turn equivalent to
$C(X_j,G^{n+1}_d)\subseteq C(X_j,E^{n+1}_d)$
is dense for each j. By Lemma 4.12, this is in turn equivalent to
![]() $\dim (X_j)<2n(d-1)$
for each j. Using that
$\dim (X_j)<2n(d-1)$
for each j. Using that
![]() $\dim (X)=\max _j\dim (X_j)$
, this is finally equivalent to (2).
$\dim (X)=\max _j\dim (X_j)$
, this is finally equivalent to (2).
Lemma 4.14 Let X be a compact metric space, let
![]() $Y\subseteq X$
be closed, and let F and
$Y\subseteq X$
be closed, and let F and
![]() $\widetilde {F}$
be continuous maps as in the diagram below such that
$\widetilde {F}$
be continuous maps as in the diagram below such that
![]() $q\circ \widetilde {F}$
agrees with F on
$q\circ \widetilde {F}$
agrees with F on
![]() $(Y\times [0,1])\cup (X\times \{0\})$
.
$(Y\times [0,1])\cup (X\times \{0\})$
.

Then, there exist
![]() $t>0$
and a continuous map
$t>0$
and a continuous map
![]() $\widetilde {H}$
making the above diagram commute.
$\widetilde {H}$
making the above diagram commute.
Proof Using that the action
![]() $\mathcal {PU}_d\curvearrowright G^{n+1}_d$
is free, it follows that the quotient map
$\mathcal {PU}_d\curvearrowright G^{n+1}_d$
is free, it follows that the quotient map
![]() $q\colon G^{n+1}_d\to G^{n+1}_d/\mathcal {PU}_d$
is the projection of a fiber bundle with base space
$q\colon G^{n+1}_d\to G^{n+1}_d/\mathcal {PU}_d$
is the projection of a fiber bundle with base space
![]() $G^{n+1}_d/\mathcal {PU}_d$
and with fibers homeomorphic to
$G^{n+1}_d/\mathcal {PU}_d$
and with fibers homeomorphic to
![]() $\mathcal {PU}_d$
. Using the homotopy lifting property for fiber bundles, we obtain
$\mathcal {PU}_d$
. Using the homotopy lifting property for fiber bundles, we obtain
![]() $H\colon X\times [0,1]\to G^{n+1}_d$
such that
$H\colon X\times [0,1]\to G^{n+1}_d$
such that
Next, we will correct H to agree with
![]() $\widetilde {F}$
on
$\widetilde {F}$
on
![]() $Y\times [0,t]$
for some
$Y\times [0,t]$
for some
![]() $t>0$
.
$t>0$
.
Given
![]() $(y,s)\in Y\times [0,1]$
, we have
$(y,s)\in Y\times [0,1]$
, we have
Let
![]() $c(y,s)\in \mathcal {PU}_d$
be the unique element such that
$c(y,s)\in \mathcal {PU}_d$
be the unique element such that
![]() $H(y,s)=c(y,s).\widetilde {F}(y,s)$
. This defines a map
$H(y,s)=c(y,s).\widetilde {F}(y,s)$
. This defines a map
![]() $c\colon Y\times [0,1]\to \mathcal {PU}_d$
. Using that the fiber bundle is locally trivial, we see that c is continuous. For every
$c\colon Y\times [0,1]\to \mathcal {PU}_d$
. Using that the fiber bundle is locally trivial, we see that c is continuous. For every
![]() $y\in Y$
, we have
$y\in Y$
, we have
![]() $H(y,0)=\widetilde {F}(y,0)$
and therefore
$H(y,0)=\widetilde {F}(y,0)$
and therefore
![]() $c(y,0)=1$
. We extend c to a map
$c(y,0)=1$
. We extend c to a map
![]() $c\colon (Y\times [0,1])\cup (X\times \{0\})\to \mathcal {PU}_d$
by setting
$c\colon (Y\times [0,1])\cup (X\times \{0\})\to \mathcal {PU}_d$
by setting
![]() $c(x,0):=1$
for every
$c(x,0):=1$
for every
![]() $x\in X$
.
$x\in X$
.
Every Lie group is a (metrizable) locally contractible, finite-dimensional space and therefore an absolute neighborhood extensor (see Theorems 1.2.7 and 4.2.33 in [Reference NagisavM01]). This allows us to extend c to a continuous map
![]() $\tilde {c}\colon U\to \mathcal {PU}_d$
defined on a neighborhood U of
$\tilde {c}\colon U\to \mathcal {PU}_d$
defined on a neighborhood U of
![]() $(Y\times [0,1])\cup (X\times \{0\})\subseteq X\times [0,1]$
. Then, define
$(Y\times [0,1])\cup (X\times \{0\})\subseteq X\times [0,1]$
. Then, define
![]() $\widetilde {H}\colon U\to G^{n+1}_d$
by
$\widetilde {H}\colon U\to G^{n+1}_d$
by
Choose
![]() $t>0$
such that
$t>0$
such that
![]() $(Y\times [0,1])\cup (X\times [0,t])\subseteq U$
. Then, the restriction of
$(Y\times [0,1])\cup (X\times [0,t])\subseteq U$
. Then, the restriction of
![]() $\widetilde {H}$
to
$\widetilde {H}$
to
![]() $(Y\times [0,1])\cup (X\times [0,t])$
has the desired properties.
$(Y\times [0,1])\cup (X\times [0,t])$
has the desired properties.
Lemma 4.15 Let A be a unital, separable, d-homogeneous
![]() $C^*\!$
-algebra,
$C^*\!$
-algebra,
![]() $d\geq 2$
. Then,
$d\geq 2$
. Then,
 $$\begin{align*}\operatorname{\mathrm{gr}}(A) = \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(A))+1}{2d-2}\right\rceil. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gr}}(A) = \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(A))+1}{2d-2}\right\rceil. \end{align*}$$
Proof Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. Since A is noncommutative, we have
$X:=\operatorname {\mathrm {Prim}}(A)$
. Since A is noncommutative, we have
![]() $\operatorname {\mathrm {gr}}(A)\geq 1$
by [Reference Thiel and WinterThi21, Proposition 5.7]. We also have
$\operatorname {\mathrm {gr}}(A)\geq 1$
by [Reference Thiel and WinterThi21, Proposition 5.7]. We also have
![]() $\left \lceil \frac {\dim (X)+1}{2d-2}\right \rceil \geq 1$
for every value of
$\left \lceil \frac {\dim (X)+1}{2d-2}\right \rceil \geq 1$
for every value of
![]() $\dim (X)$
. Thus, it is enough to show that, for every
$\dim (X)$
. Thus, it is enough to show that, for every
![]() $n\geq 1$
, the following holds:
$n\geq 1$
, the following holds:
Recall that we use
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
to denote the set of injective continuous maps
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
to denote the set of injective continuous maps
![]() $X\to G^{n+1}_d/\mathcal {PU}_d$
. As explained in Paragraph 4.3, we have the following inclusions and maps:
$X\to G^{n+1}_d/\mathcal {PU}_d$
. As explained in Paragraph 4.3, we have the following inclusions and maps:

Assume that
![]() $\operatorname {\mathrm {gr}}(A)\leq n$
. Since A is separable, it follows from Theorem 2.2 that
$\operatorname {\mathrm {gr}}(A)\leq n$
. Since A is separable, it follows from Theorem 2.2 that
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is dense. Since
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is dense. Since
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, we deduce from Lemma 4.13 that
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}\subseteq \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, we deduce from Lemma 4.13 that
![]() $\dim (X)<2n(d-1)$
.
$\dim (X)<2n(d-1)$
.
Conversely, assume that
![]() $\dim (X)<2n(d-1)$
. Applying Lemma 4.13, we see that
$\dim (X)<2n(d-1)$
. Applying Lemma 4.13, we see that
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is dense and open. Furthermore, by Proposition 4.1, a tuple
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}\subseteq A^{n+1}_{\mathrm {sa}}$
is dense and open. Furthermore, by Proposition 4.1, a tuple
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
belongs to
$\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
belongs to
![]() $\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if
$\operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
if and only if
![]() $\Psi (\mathbf {a})$
belongs to
$\Psi (\mathbf {a})$
belongs to
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
. Thus, to verify
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
. Thus, to verify
![]() $\operatorname {\mathrm {gr}}(A)\leq n$
, it suffices to show the following.
$\operatorname {\mathrm {gr}}(A)\leq n$
, it suffices to show the following.
Let
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
and
$\mathbf {a}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
and
![]() $\varepsilon>0$
. Then, there exists
$\varepsilon>0$
. Then, there exists
![]() $\mathbf {b}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
such that
$\mathbf {b}\in \operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
such that
By [Reference LuukkainenLuu81, Theorem 5.1], if M is a metrizable manifold with
![]() $2\dim (X)<\dim (M)$
, then
$2\dim (X)<\dim (M)$
, then
![]() $E(X,M)\subseteq C(X,M)$
is dense with respect to the metric
$E(X,M)\subseteq C(X,M)$
is dense with respect to the metric
![]() $d(f,g)=\sup \{d_M(f(x),g(x)):x\in X\}$
, where
$d(f,g)=\sup \{d_M(f(x),g(x)):x\in X\}$
, where
![]() $d_M$
is a metric inducing the topology on M.
$d_M$
is a metric inducing the topology on M.
By Lemma 4.9,
![]() $G^{n+1}_d$
is an open subset of
$G^{n+1}_d$
is an open subset of
![]() $E^{n+1}_d$
and therefore is a manifold of dimension
$E^{n+1}_d$
and therefore is a manifold of dimension
![]() $(n+1)d^2$
. Furthermore,
$(n+1)d^2$
. Furthermore,
![]() $\mathcal {PU}_d$
is a compact Lie group of dimension
$\mathcal {PU}_d$
is a compact Lie group of dimension
![]() $d^2-1$
, acting freely on
$d^2-1$
, acting freely on
![]() $G^{n+1}_d$
. Hence, as noted in the proof of Lemma 4.11, it follows from [Reference BredonBre72, Theorem IV.3.8] that
$G^{n+1}_d$
. Hence, as noted in the proof of Lemma 4.11, it follows from [Reference BredonBre72, Theorem IV.3.8] that
![]() $G^{n+1}_d/\mathcal {PU}_d$
is a manifold of dimension
$G^{n+1}_d/\mathcal {PU}_d$
is a manifold of dimension
![]() $(n+1)d^2- (d^2-1)=nd^2+1$
. By assumption, we have
$(n+1)d^2- (d^2-1)=nd^2+1$
. By assumption, we have
![]() $\dim (X)<2n(d-1)$
, and thus
$\dim (X)<2n(d-1)$
, and thus
It follows that
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
is dense in
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
is dense in
![]() $C(X,G^{n+1}_d/\mathcal {PU}_d)$
.
$C(X,G^{n+1}_d/\mathcal {PU}_d)$
.
Set
![]() $f:=\Psi (\mathbf {a})$
. Then,
$f:=\Psi (\mathbf {a})$
. Then,
![]() $f\colon X\to G^{n+1}_d/\mathcal {PU}_d$
is a continuous map, which can be approximated arbitrarily closely by embeddings. To complete the proof, we need to show that one of these embeddings is realized as
$f\colon X\to G^{n+1}_d/\mathcal {PU}_d$
is a continuous map, which can be approximated arbitrarily closely by embeddings. To complete the proof, we need to show that one of these embeddings is realized as
![]() $\Psi (\mathbf {b})$
for some
$\Psi (\mathbf {b})$
for some
![]() $\mathbf {b}\in A^{n+1}_{\mathrm {sa}}$
close to
$\mathbf {b}\in A^{n+1}_{\mathrm {sa}}$
close to
![]() $\mathbf {a}$
. We will do this by successively applying our version of the homotopy extension lifting property proved in Lemma 4.14.
$\mathbf {a}$
. We will do this by successively applying our version of the homotopy extension lifting property proved in Lemma 4.14.
Every manifold is finite-dimensional and locally contractible and therefore an absolute neighborhood retract (ANR) (see [Reference NagisavM01, Theorem 4.2.33]). Given a homotopy
![]() $H\colon X\times [0,1]\to M$
and
$H\colon X\times [0,1]\to M$
and
![]() $t\in [0,1]$
, we let
$t\in [0,1]$
, we let
![]() $H_t\colon X\to M$
be given by
$H_t\colon X\to M$
be given by
![]() $H_t(x):=H(x,t)$
.
$H_t(x):=H(x,t)$
.
Step 1: We find a homotopy
![]() $F\colon X\times [0,1]\to G^{n+1}_d/\mathcal {PU}_d$
such that
$F\colon X\times [0,1]\to G^{n+1}_d/\mathcal {PU}_d$
such that
![]() $F_0=f$
and such that
$F_0=f$
and such that
![]() $F_{1/k}$
belongs to
$F_{1/k}$
belongs to
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
for every
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
for every
![]() $k\geq 1$
.
$k\geq 1$
.
Set
![]() $M:=G^{n+1}_d/\mathcal {PU}_d$
. We use that M is an ANR. Given
$M:=G^{n+1}_d/\mathcal {PU}_d$
. We use that M is an ANR. Given
![]() $\delta>0$
, one says that
$\delta>0$
, one says that
![]() $H\colon X\times [0,1]\to M$
is a
$H\colon X\times [0,1]\to M$
is a
![]() $\delta $
-homotopy if
$\delta $
-homotopy if
![]() $d(H_0,H_t)<\delta $
for all
$d(H_0,H_t)<\delta $
for all
![]() $t\in [0,1]$
. By [Reference NagisavM01, Theorem 4.1.1], for every
$t\in [0,1]$
. By [Reference NagisavM01, Theorem 4.1.1], for every
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $\gamma>0$
such that, for every
$\gamma>0$
such that, for every
![]() $g\in C(X,M)$
satisfying
$g\in C(X,M)$
satisfying
![]() $d(f,g)<\gamma $
, there exists a
$d(f,g)<\gamma $
, there exists a
![]() $\delta $
-homotopy
$\delta $
-homotopy
![]() $H\colon X\times [0,1]\to M$
with
$H\colon X\times [0,1]\to M$
with
![]() $H_0=f$
and
$H_0=f$
and
![]() $H_1=g$
. Given
$H_1=g$
. Given
![]() $n\in \mathbb {N}$
, we apply this for
$n\in \mathbb {N}$
, we apply this for
![]() $\delta _n=\tfrac {1}{2^n}$
, to obtain
$\delta _n=\tfrac {1}{2^n}$
, to obtain
![]() $\gamma _n>0$
. Using that
$\gamma _n>0$
. Using that
![]() $E(X,M)\subseteq C(X,M)$
is dense, choose
$E(X,M)\subseteq C(X,M)$
is dense, choose
![]() $g_n\in E(X,M)$
satisfying
$g_n\in E(X,M)$
satisfying
![]() $d(f,g_n)<\gamma _n$
. By choice of
$d(f,g_n)<\gamma _n$
. By choice of
![]() $\gamma _n$
, we obtain a
$\gamma _n$
, we obtain a
![]() $\tfrac {1}{2^n}$
-homotopy
$\tfrac {1}{2^n}$
-homotopy
![]() $H^{(n)}\colon X\times [0,1]\to M$
satisfying
$H^{(n)}\colon X\times [0,1]\to M$
satisfying
![]() $H^{(n)}_0=f$
and
$H^{(n)}_0=f$
and
![]() $H^{(n)}_1=g_n$
.
$H^{(n)}_1=g_n$
.
Next, we define
![]() $H\colon X\times [0,\infty )\to M$
by
$H\colon X\times [0,\infty )\to M$
by
 $$\begin{align*}H(x,t) = \begin{cases} H^{(k)}(x,2k+1-t), &\text{ if } t\in[2k,2k+1], \\ H^{(k+1)}(x,t-2k-1), &\text{ if } t\in[2k+1,2k+2]. \end{cases} \end{align*}$$
$$\begin{align*}H(x,t) = \begin{cases} H^{(k)}(x,2k+1-t), &\text{ if } t\in[2k,2k+1], \\ H^{(k+1)}(x,t-2k-1), &\text{ if } t\in[2k+1,2k+2]. \end{cases} \end{align*}$$
Thus, H is the concatenation of the reverse of
![]() $H^{(1)}$
, followed by
$H^{(1)}$
, followed by
![]() $H^{(2)}$
and its reverse, and so on, as shown in the following picture:
$H^{(2)}$
and its reverse, and so on, as shown in the following picture:

Note that
![]() $H(\_\,,2k)=g_k$
for each
$H(\_\,,2k)=g_k$
for each
![]() $k\in \mathbb {N}$
, and
$k\in \mathbb {N}$
, and
![]() $\lim _{t\to \infty }H(x,t)=f(x)$
for every
$\lim _{t\to \infty }H(x,t)=f(x)$
for every
![]() $x\in X$
. Let
$x\in X$
. Let
![]() $\varrho \colon (0,1]\to [0,\infty )$
be a strictly decreasing, continuous map satisfying
$\varrho \colon (0,1]\to [0,\infty )$
be a strictly decreasing, continuous map satisfying
![]() $\varrho (\tfrac {1}{k})=2k-2$
for
$\varrho (\tfrac {1}{k})=2k-2$
for
![]() $k\geq 1$
. Then,
$k\geq 1$
. Then,
![]() $F\colon X\times [0,1]$
defined by
$F\colon X\times [0,1]$
defined by
![]() $F(x,0)=f(x)$
and
$F(x,0)=f(x)$
and
![]() $F(x,t)=H(x,\varrho (t))$
for
$F(x,t)=H(x,\varrho (t))$
for
![]() $t\in (0,1]$
has the desired properties.
$t\in (0,1]$
has the desired properties.
Step 2: Since X is compact, and since the
![]() $M_d$
-bundle associated with A is locally trivial, we can choose closed subsets
$M_d$
-bundle associated with A is locally trivial, we can choose closed subsets
![]() $X_1,\ldots ,X_m\subseteq X$
that cover X such that
$X_1,\ldots ,X_m\subseteq X$
that cover X such that
![]() $A(X_j)\cong C(X_j,M_d)$
for each j. Let
$A(X_j)\cong C(X_j,M_d)$
for each j. Let
![]() $\pi _j\colon A\to C(X_j,M_d)$
be the corresponding quotient map. Abusing notation, we also use
$\pi _j\colon A\to C(X_j,M_d)$
be the corresponding quotient map. Abusing notation, we also use
![]() $\pi _j$
to denote the naturally induced map
$\pi _j$
to denote the naturally induced map
Given
![]() $j,k\in \{1,\ldots ,m\}$
, both
$j,k\in \{1,\ldots ,m\}$
, both
![]() $\pi _j$
and
$\pi _j$
and
![]() $\pi _k$
induce an isomorphism between
$\pi _k$
induce an isomorphism between
![]() $A(X_j\cap X_k)$
and
$A(X_j\cap X_k)$
and
![]() $C(X_j\cap X_k,M_d)$
. Let
$C(X_j\cap X_k,M_d)$
. Let
![]() $c_{k,j}\colon X_j\cap X_k\to \mathcal {PU}_d=\operatorname {\mathrm {Aut}}(M_d)$
be the continuous map such that
$c_{k,j}\colon X_j\cap X_k\to \mathcal {PU}_d=\operatorname {\mathrm {Aut}}(M_d)$
be the continuous map such that
![]() $c_{k,j}(x).\pi _j(e)(x)=\pi _k(e)(x)$
for every
$c_{k,j}(x).\pi _j(e)(x)=\pi _k(e)(x)$
for every
![]() $e\in A$
and
$e\in A$
and
![]() $x\in X_j\cap X_k$
. Then,
$x\in X_j\cap X_k$
. Then,
for every
![]() $\mathbf {e}\in A^{n+1}_{\mathrm {sa}}$
and
$\mathbf {e}\in A^{n+1}_{\mathrm {sa}}$
and
![]() $x\in X_j\cap X_k$
.
$x\in X_j\cap X_k$
.
Step 3: We will successively choose
![]() $t_1\geq t_2\geq \cdots \geq t_m>0$
and continuous maps
$t_1\geq t_2\geq \cdots \geq t_m>0$
and continuous maps
such that
and such that, for every
![]() $j\leq k$
and
$j\leq k$
and
![]() $(x,s)\in (X_j\cap X_k)\times [0,t_k]$
, we have
$(x,s)\in (X_j\cap X_k)\times [0,t_k]$
, we have
We start by setting
![]() $t_1:=1$
. The map
$t_1:=1$
. The map
![]() $\pi _1(\mathbf {a})\colon X_1\to G^{n+1}_d$
satisfies
$\pi _1(\mathbf {a})\colon X_1\to G^{n+1}_d$
satisfies
![]() $q\circ \pi _1(\mathbf {a})=f|_{X_1}$
. Thus,
$q\circ \pi _1(\mathbf {a})=f|_{X_1}$
. Thus,
![]() $\pi _1(\mathbf {a})$
is a lift of
$\pi _1(\mathbf {a})$
is a lift of
![]() $F|_{X_1\times \{0\}}$
. Using the homotopy lifting property for fiber bundles, we obtain
$F|_{X_1\times \{0\}}$
. Using the homotopy lifting property for fiber bundles, we obtain
![]() $H^{(1)}\colon X_1\times [0,1]\to G^{n+1}_d$
such that
$H^{(1)}\colon X_1\times [0,1]\to G^{n+1}_d$
such that
Next, assume that we have chosen
![]() $t_1\geq \cdots \geq t_{k-1}$
and
$t_1\geq \cdots \geq t_{k-1}$
and
![]() $H^{(j)}$
for
$H^{(j)}$
for
![]() $j=1,\ldots ,k-1$
. Set
$j=1,\ldots ,k-1$
. Set
![]() $Y_k:= X_k\cap (X_1\cup \cdots \cup X_{k-1})$
, which is a closed subset of
$Y_k:= X_k\cap (X_1\cup \cdots \cup X_{k-1})$
, which is a closed subset of
![]() $X_k$
. We define
$X_k$
. We define
![]() $\widetilde {F}^{(k)}\colon (Y_{k}\times [0,t_{k-1}])\cup (X_{k}\times \{0\})\to G^{n+1}_d$
by
$\widetilde {F}^{(k)}\colon (Y_{k}\times [0,t_{k-1}])\cup (X_{k}\times \{0\})\to G^{n+1}_d$
by
 $$\begin{align*}\widetilde{F}^{(k)}(x,t) := \begin{cases} c_{k,j}(x).H^{(j)}(x,t), & \text{ if } x\in X_{k}\cap X_j, \text{for } j\leq k-1, \\ \pi_{k}(\mathbf{a})(x), & \text{ if } t=0. \end{cases} \end{align*}$$
$$\begin{align*}\widetilde{F}^{(k)}(x,t) := \begin{cases} c_{k,j}(x).H^{(j)}(x,t), & \text{ if } x\in X_{k}\cap X_j, \text{for } j\leq k-1, \\ \pi_{k}(\mathbf{a})(x), & \text{ if } t=0. \end{cases} \end{align*}$$
It follows from (4.5) that
![]() $\widetilde {F}^{(k)}$
is well defined. Furthermore, using (4.4), we obtain that
$\widetilde {F}^{(k)}$
is well defined. Furthermore, using (4.4), we obtain that
![]() $q\circ \widetilde {F}^{(k)}$
and F agree on
$q\circ \widetilde {F}^{(k)}$
and F agree on
![]() $(Y_{k}\times [0,t_{k-1}])\cup (X_k\times \{0\})$
. Applying Lemma 4.14, we obtain
$(Y_{k}\times [0,t_{k-1}])\cup (X_k\times \{0\})$
. Applying Lemma 4.14, we obtain
![]() $t_k\in (0,t_{k-1}]$
and
$t_k\in (0,t_{k-1}]$
and
![]() $H^{(k)}$
making the following diagram commute:
$H^{(k)}$
making the following diagram commute:

One checks that
![]() $H^{(k)}$
has the desired properties.
$H^{(k)}$
has the desired properties.
Step 4: Let
![]() $t\in [0,t_m]$
. For each
$t\in [0,t_m]$
. For each
![]() $j\in \{1,\ldots ,m\}$
, the map
$j\in \{1,\ldots ,m\}$
, the map
![]() $H^{(j)}_t\colon X_j\to G^{n+1}_d$
defines an element in
$H^{(j)}_t\colon X_j\to G^{n+1}_d$
defines an element in
![]() $\mathbf {b}_t^{(j)}\in C(X_j,M_d)^{n+1}_{\mathrm {sa}}$
. Given
$\mathbf {b}_t^{(j)}\in C(X_j,M_d)^{n+1}_{\mathrm {sa}}$
. Given
![]() $j\leq k$
in
$j\leq k$
in
![]() $\{1,\ldots ,m\}$
and
$\{1,\ldots ,m\}$
and
![]() $x\in X_j\cap X_k$
, it follows from (4.5) that
$x\in X_j\cap X_k$
, it follows from (4.5) that
Thus,
![]() $\mathbf {b}_t^{(1)},\ldots ,\mathbf {b}_t^{(m)}$
can be patched to give
$\mathbf {b}_t^{(1)},\ldots ,\mathbf {b}_t^{(m)}$
can be patched to give
![]() $\mathbf {b}_t\in A^{n+1}_{\mathrm {sa}}$
such that
$\mathbf {b}_t\in A^{n+1}_{\mathrm {sa}}$
such that
![]() $\mathbf {b}_t^{(j)}=\pi _j(\mathbf {b}_t)$
for each j. One checks that each
$\mathbf {b}_t^{(j)}=\pi _j(\mathbf {b}_t)$
for each j. One checks that each
![]() $\mathbf {b}_t^{(j)}$
depends continuously on t, which implies that the map
$\mathbf {b}_t^{(j)}$
depends continuously on t, which implies that the map
![]() $[0,t_m]\to A^{n+1}_{\mathrm {sa}}$
,
$[0,t_m]\to A^{n+1}_{\mathrm {sa}}$
,
![]() $t\mapsto \mathbf {b}_t$
, is continuous. By construction, we have
$t\mapsto \mathbf {b}_t$
, is continuous. By construction, we have
![]() $\mathbf {b}_0=\mathbf {a}$
, and
$\mathbf {b}_0=\mathbf {a}$
, and
![]() $\Psi (\mathbf {b}_t)=F_t$
for each
$\Psi (\mathbf {b}_t)=F_t$
for each
![]() $t\in [0,t_m]$
. Using that
$t\in [0,t_m]$
. Using that
![]() $\mathbf {a}$
belongs to
$\mathbf {a}$
belongs to
![]() $\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, which is an open subset of
$\operatorname {\mathrm {Gen}}^{\mathrm {fiber}}_{n+1}(A)_{\mathrm {sa}}$
, which is an open subset of
![]() $A^{n+1}_{\mathrm {sa}}$
, we can choose
$A^{n+1}_{\mathrm {sa}}$
, we can choose
![]() $k\geq 1$
such that
$k\geq 1$
such that
We have
![]() $\Psi (\mathbf {b}_{1/k})=F_{1/k}$
, which by construction of F (Step 1) belongs to
$\Psi (\mathbf {b}_{1/k})=F_{1/k}$
, which by construction of F (Step 1) belongs to
![]() $E(X,G^{n+1}_d/\mathcal {PU}_d)$
. It follows that
$E(X,G^{n+1}_d/\mathcal {PU}_d)$
. It follows that
![]() $\mathbf {b}_{1/k}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
.
$\mathbf {b}_{1/k}\in \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
.
Proposition 4.16 Let A be a unital d-homogeneous
![]() $C^*\!$
-algebra,
$C^*\!$
-algebra,
![]() $d\geq 2$
. Then,
$d\geq 2$
. Then,
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(A))+1}{2d-2}\right\rceil. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(A))+1}{2d-2}\right\rceil. \end{align*} $$
Proof Set
![]() $n:=\operatorname {\mathrm {gr}}(A)$
and
$n:=\operatorname {\mathrm {gr}}(A)$
and
![]() $l:=\dim (\operatorname {\mathrm {Prim}}(A))$
, and then set
$l:=\dim (\operatorname {\mathrm {Prim}}(A))$
, and then set
 $$ \begin{align*} \mathcal{S}_1 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : 1\in B, \operatorname{\mathrm{gr}}(B)\leq n \big\}, \quad\text{ and }\quad \\ \mathcal{S}_2 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : B\ d\text{-homogeneous}, \operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(B))\leq l \big\}. \end{align*} $$
$$ \begin{align*} \mathcal{S}_1 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : 1\in B, \operatorname{\mathrm{gr}}(B)\leq n \big\}, \quad\text{ and }\quad \\ \mathcal{S}_2 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : B\ d\text{-homogeneous}, \operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(B))\leq l \big\}. \end{align*} $$
As noted in Paragraph 3.1, since
![]() $\operatorname {\mathrm {gr}}$
satisfies (D5) and (D6), it follows that
$\operatorname {\mathrm {gr}}$
satisfies (D5) and (D6), it follows that
![]() $\mathcal {S}_1$
is
$\mathcal {S}_1$
is
![]() $\sigma $
-complete and cofinal. By Proposition 3.5,
$\sigma $
-complete and cofinal. By Proposition 3.5,
![]() $\mathcal {S}_2$
is
$\mathcal {S}_2$
is
![]() $\sigma $
-complete and cofinal. Hence,
$\sigma $
-complete and cofinal. Hence,
![]() $\mathcal {S}_1\cap \mathcal {S}_2$
is
$\mathcal {S}_1\cap \mathcal {S}_2$
is
![]() $\sigma $
-complete and cofinal as well.
$\sigma $
-complete and cofinal as well.
Let
![]() $B\in \mathcal {S}_1\cap \mathcal {S}_2$
. Then, B is a unital, separable, d-homogeneous
$B\in \mathcal {S}_1\cap \mathcal {S}_2$
. Then, B is a unital, separable, d-homogeneous
![]() $C^*\!$
-algebra. Hence,
$C^*\!$
-algebra. Hence,
![]() $\dim (\operatorname {\mathrm {Prim}}(B))=\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))$
, and by Lemma 4.15, we have
$\dim (\operatorname {\mathrm {Prim}}(B))=\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(B))$
, and by Lemma 4.15, we have
 $$\begin{align*}\operatorname{\mathrm{gr}}(B) = \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(B))+1}{2d-2}\right\rceil. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gr}}(B) = \left\lceil\frac{\dim(\operatorname{\mathrm{Prim}}(B))+1}{2d-2}\right\rceil. \end{align*}$$
Thus, each
![]() $B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
$B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
![]() $\operatorname {\mathrm {gr}}(B)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
. Since A is approximated by the family
$\operatorname {\mathrm {gr}}(B)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
. Since A is approximated by the family
![]() $\mathcal {S}_1\cap \mathcal {S}_2$
, we obtain
$\mathcal {S}_1\cap \mathcal {S}_2$
, we obtain
![]() $\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
by Theorem 2.6.
$\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
by Theorem 2.6.
To show the converse inequality, set
Then, each
![]() $B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
$B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
![]() $\operatorname {\mathrm {topdim}}(B)=\dim (\operatorname {\mathrm {Prim}}(B))\leq m$
. Arguing with the topological dimension as in the proof of Lemma 3.4, we deduce that
$\operatorname {\mathrm {topdim}}(B)=\dim (\operatorname {\mathrm {Prim}}(B))\leq m$
. Arguing with the topological dimension as in the proof of Lemma 3.4, we deduce that
![]() $\dim (\operatorname {\mathrm {Prim}}(A))=\operatorname {\mathrm {topdim}}(A)\leq m$
, and thus
$\dim (\operatorname {\mathrm {Prim}}(A))=\operatorname {\mathrm {topdim}}(A)\leq m$
, and thus
![]() $n\geq \left \lceil \frac {\dim (\operatorname {\mathrm {Prim}}(A))+1}{2d-2}\right \rceil $
, as desired.
$n\geq \left \lceil \frac {\dim (\operatorname {\mathrm {Prim}}(A))+1}{2d-2}\right \rceil $
, as desired.
Theorem 4.17 Let A be a d-homogeneous
![]() $C^*\!$
-algebra. Set
$C^*\!$
-algebra. Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. If
$X:=\operatorname {\mathrm {Prim}}(A)$
. If
![]() $d=1$
, then
$d=1$
, then
![]() $\operatorname {\mathrm {gr}}_0(A)=\operatorname {\mathrm {gr}}(A) = \operatorname {\mathrm {locdim}}(X\times X)$
. If
$\operatorname {\mathrm {gr}}_0(A)=\operatorname {\mathrm {gr}}(A) = \operatorname {\mathrm {locdim}}(X\times X)$
. If
![]() $d\geq 2$
, then
$d\geq 2$
, then
 $$ \begin{align*} \operatorname{\mathrm{gr}}_0(A)=\operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}_0(A)=\operatorname{\mathrm{gr}}(A) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil. \end{align*} $$
Proof For
![]() $d=1$
, this follows from Theorem 2.7. So assume that
$d=1$
, this follows from Theorem 2.7. So assume that
![]() $d\geq 2$
. By Proposition 2.4, we have
$d\geq 2$
. By Proposition 2.4, we have
![]() $\operatorname {\mathrm {gr}}_0(A) \leq \operatorname {\mathrm {gr}}(A)$
. Let
$\operatorname {\mathrm {gr}}_0(A) \leq \operatorname {\mathrm {gr}}(A)$
. Let
![]() $K\subseteq X$
be a compact subset. The corresponding quotient
$K\subseteq X$
be a compact subset. The corresponding quotient
![]() $A(K)$
is a unital d-homogeneous
$A(K)$
is a unital d-homogeneous
![]() $C^*\!$
-algebra with
$C^*\!$
-algebra with
![]() $\operatorname {\mathrm {Prim}}(A(K))\cong K$
. Using Proposition 4.16 at the first step, and using Theorem 2.5 at the last step, we get
$\operatorname {\mathrm {Prim}}(A(K))\cong K$
. Using Proposition 4.16 at the first step, and using Theorem 2.5 at the last step, we get
 $$\begin{align*}\left\lceil\frac{\dim(K)+1}{2d-2}\right\rceil = \operatorname{\mathrm{gr}}(A(K)) = \operatorname{\mathrm{gr}}_0(A(K)) \leq \operatorname{\mathrm{gr}}_0(A). \end{align*}$$
$$\begin{align*}\left\lceil\frac{\dim(K)+1}{2d-2}\right\rceil = \operatorname{\mathrm{gr}}(A(K)) = \operatorname{\mathrm{gr}}_0(A(K)) \leq \operatorname{\mathrm{gr}}_0(A). \end{align*}$$
Since this holds for every compact subset of X, we deduce that
 $$\begin{align*}\left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil \leq \operatorname{\mathrm{gr}}_0(A) \leq \operatorname{\mathrm{gr}}(A). \end{align*}$$
$$\begin{align*}\left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil \leq \operatorname{\mathrm{gr}}_0(A) \leq \operatorname{\mathrm{gr}}(A). \end{align*}$$
To verify that
![]() $\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {\operatorname {\mathrm {locdim}}(X)+1}{2d-2}\right \rceil $
, set
$\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {\operatorname {\mathrm {locdim}}(X)+1}{2d-2}\right \rceil $
, set
![]() $l:=\operatorname {\mathrm {locdim}}(X)$
, which we may assume to be finite. By Proposition 3.5, the collection
$l:=\operatorname {\mathrm {locdim}}(X)$
, which we may assume to be finite. By Proposition 3.5, the collection
is
![]() $\sigma $
-complete and cofinal. Let
$\sigma $
-complete and cofinal. Let
![]() $B\in \mathcal {S}$
. We view B as a locally trivial
$B\in \mathcal {S}$
. We view B as a locally trivial
![]() $M_d$
-bundle over
$M_d$
-bundle over
![]() $Y:=\operatorname {\mathrm {Prim}}(B)$
. Since B is separable, Y is
$Y:=\operatorname {\mathrm {Prim}}(B)$
. Since B is separable, Y is
![]() $\sigma $
-compact and thus
$\sigma $
-compact and thus
![]() $\dim (Y)=\operatorname {\mathrm {locdim}}(Y)\leq l<\infty $
. By [Reference ThielPhi07, Lemma 2.5], the
$\dim (Y)=\operatorname {\mathrm {locdim}}(Y)\leq l<\infty $
. By [Reference ThielPhi07, Lemma 2.5], the
![]() $M_d$
-bundle has finite type. Applying [Reference ThielPhi07, Proposition 2.9], we obtain a locally trivial
$M_d$
-bundle has finite type. Applying [Reference ThielPhi07, Proposition 2.9], we obtain a locally trivial
![]() $M_d$
-bundle over the Stone–Čech-compactification
$M_d$
-bundle over the Stone–Čech-compactification
![]() $\beta Y$
extending the bundle associated with B. This means that there is a unital d-homogeneous
$\beta Y$
extending the bundle associated with B. This means that there is a unital d-homogeneous
![]() $C^*\!$
-algebra D with
$C^*\!$
-algebra D with
![]() $\operatorname {\mathrm {Prim}}(D)\cong \beta (Y)$
such that B is an ideal in D. Since Y is a normal space, we have
$\operatorname {\mathrm {Prim}}(D)\cong \beta (Y)$
such that B is an ideal in D. Since Y is a normal space, we have
![]() $\dim (\beta Y)=\dim (Y)$
by [Reference PhillipsPea75, Proposition 6.4.3, p. 232]. Using Theorem 2.5 at the first step, and Proposition 4.16 at the second step, we get
$\dim (\beta Y)=\dim (Y)$
by [Reference PhillipsPea75, Proposition 6.4.3, p. 232]. Using Theorem 2.5 at the first step, and Proposition 4.16 at the second step, we get
 $$\begin{align*}\operatorname{\mathrm{gr}}(B) \leq\operatorname{\mathrm{gr}}(D) = \left\lceil\frac{\dim(\beta Y)+1}{2d-2}\right\rceil \leq \left\lceil\frac{l+1}{2d-2}\right\rceil. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gr}}(B) \leq\operatorname{\mathrm{gr}}(D) = \left\lceil\frac{\dim(\beta Y)+1}{2d-2}\right\rceil \leq \left\lceil\frac{l+1}{2d-2}\right\rceil. \end{align*}$$
Since A is approximated by
![]() $\mathcal {S}$
, we obtain
$\mathcal {S}$
, we obtain
![]() $\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
by Theorem 2.6.
$\operatorname {\mathrm {gr}}(A)\leq \left \lceil \tfrac {l+1}{2d-2}\right \rceil $
by Theorem 2.6.
In Corollary 5.7, we will generalize the following result to compute the generator rank of direct sums of subhomogeneous
![]() $C^*\!$
-algebras.
$C^*\!$
-algebras.
Lemma 4.18 Let A and B be d-homogeneous
![]() $C^*\!$
-algebras. Then,
$C^*\!$
-algebras. Then,
Proof For
![]() $d=1$
, this follows from [Reference Thiel and WinterThi21, Proposition 5.9]. So assume that
$d=1$
, this follows from [Reference Thiel and WinterThi21, Proposition 5.9]. So assume that
![]() $d\geq 2$
. Set
$d\geq 2$
. Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
, and
$X:=\operatorname {\mathrm {Prim}}(A)$
, and
![]() $Y:=\operatorname {\mathrm {Prim}}(B)$
. Then,
$Y:=\operatorname {\mathrm {Prim}}(B)$
. Then,
![]() $A\oplus B$
is d-homogeneous with
$A\oplus B$
is d-homogeneous with
![]() $\operatorname {\mathrm {Prim}}(A\oplus B)\cong X\sqcup Y$
, the disjoint union of X and Y. Applying Theorem 4.17 at the first and last steps, we obtain
$\operatorname {\mathrm {Prim}}(A\oplus B)\cong X\sqcup Y$
, the disjoint union of X and Y. Applying Theorem 4.17 at the first and last steps, we obtain
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A\oplus B) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X\sqcup Y)+1}{2d-2}\right\rceil = \left\lceil\frac{\max\{\operatorname{\mathrm{locdim}}(X),\operatorname{\mathrm{locdim}}(Y)\}+1}{2d-2}\right\rceil \\ &= \max\left\{ \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil, \left\lceil\frac{\operatorname{\mathrm{locdim}}(Y)+1}{2d-2}\right\rceil \right\} \\ &=\max\big\{ \operatorname{\mathrm{gr}}(A),\operatorname{\mathrm{gr}}(B) \big\}.\\[-32pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A\oplus B) &= \left\lceil\frac{\operatorname{\mathrm{locdim}}(X\sqcup Y)+1}{2d-2}\right\rceil = \left\lceil\frac{\max\{\operatorname{\mathrm{locdim}}(X),\operatorname{\mathrm{locdim}}(Y)\}+1}{2d-2}\right\rceil \\ &= \max\left\{ \left\lceil\frac{\operatorname{\mathrm{locdim}}(X)+1}{2d-2}\right\rceil, \left\lceil\frac{\operatorname{\mathrm{locdim}}(Y)+1}{2d-2}\right\rceil \right\} \\ &=\max\big\{ \operatorname{\mathrm{gr}}(A),\operatorname{\mathrm{gr}}(B) \big\}.\\[-32pt] \end{align*} $$
Remark 4.19 Let A be a unital d-homogeneous
![]() $C^*\!$
-algebra. Set
$C^*\!$
-algebra. Set
![]() $X:=\operatorname {\mathrm {Prim}}(A)$
. If
$X:=\operatorname {\mathrm {Prim}}(A)$
. If
![]() $d\,{=}\,1$
, then
$d\,{=}\,1$
, then
![]() $A\cong C(X)$
, and by Theorem 2.7, the generator rank of A is
$A\cong C(X)$
, and by Theorem 2.7, the generator rank of A is
![]() $\dim (X\times X)$
. The value of
$\dim (X\times X)$
. The value of
![]() $\dim (X\times X)$
is either
$\dim (X\times X)$
is either
![]() $2\dim (X)$
or
$2\dim (X)$
or
![]() $2\dim (X)-1$
, and accordingly we say that X is of basic type or of exceptional type (see [Reference Thiel and WinterThi21, Proposition 5.3]).
$2\dim (X)-1$
, and accordingly we say that X is of basic type or of exceptional type (see [Reference Thiel and WinterThi21, Proposition 5.3]).
If
![]() $d\geq 2$
, then by Proposition 4.16, the generator rank of A only depends on
$d\geq 2$
, then by Proposition 4.16, the generator rank of A only depends on
![]() $\dim (X)$
(and d), but not on
$\dim (X)$
(and d), but not on
![]() $\dim (X\times X)$
. Thus, in this case, the generator rank of A does not depend on whether X is of basic or exceptional type.
$\dim (X\times X)$
. Thus, in this case, the generator rank of A does not depend on whether X is of basic or exceptional type.
Remark 4.20 Let
![]() $m\geq 1$
and
$m\geq 1$
and
![]() $d\geq 2$
, and set
$d\geq 2$
, and set
![]() $A=C([0,1]^m,M_d)$
. Let
$A=C([0,1]^m,M_d)$
. Let
![]() $\mathrm {gen}(A)$
denote the minimal number of self-adjoint generators for A. By [Reference Ng and WinterNag04, Theorem 4], [Reference Beggs and EvansBE91, Corollary 3.2] (see also [Reference BlackadarBla06, Theorem V.3.2.6]), and Proposition 4.16, we have
$\mathrm {gen}(A)$
denote the minimal number of self-adjoint generators for A. By [Reference Ng and WinterNag04, Theorem 4], [Reference Beggs and EvansBE91, Corollary 3.2] (see also [Reference BlackadarBla06, Theorem V.3.2.6]), and Proposition 4.16, we have
5 Subhomogeneous
 $C^*\!$
-algebras
$C^*\!$
-algebras
In this section, we compute the generator rank of subhomogeneous
![]() $C^*\!$
-algebras (see Theorem 5.5). Recall that a
$C^*\!$
-algebras (see Theorem 5.5). Recall that a
![]() $C^*\!$
-algebra is d-subhomogeneous (for some
$C^*\!$
-algebra is d-subhomogeneous (for some
![]() $d\geq 1$
) if all of its irreducible representations have dimension at most d, and it is subhomogeneous if it is d-subhomogeneous for some d (see [Reference BlackadarBla06, Definition IV.1.4.1, p. 330]). It is known that a
$d\geq 1$
) if all of its irreducible representations have dimension at most d, and it is subhomogeneous if it is d-subhomogeneous for some d (see [Reference BlackadarBla06, Definition IV.1.4.1, p. 330]). It is known that a
![]() $C^*\!$
-algebra is subhomogeneous if and only if it is a sub-
$C^*\!$
-algebra is subhomogeneous if and only if it is a sub-
![]() $C^*\!$
-algebra of a homogeneous
$C^*\!$
-algebra of a homogeneous
![]() $C^*\!$
-algebra; equivalently, it is a sub-
$C^*\!$
-algebra; equivalently, it is a sub-
![]() $C^*\!$
-algebra of
$C^*\!$
-algebra of
![]() $C(X,M_d)$
for some compact Hausdorff space X and some
$C(X,M_d)$
for some compact Hausdorff space X and some
![]() $d\geq 1$
.
$d\geq 1$
.
Inductive limits of subhomogeneous
![]() $C^*\!$
-algebras are called ASH-algebras. As an application, we show that every nonzero,
$C^*\!$
-algebras are called ASH-algebras. As an application, we show that every nonzero,
![]() $\mathcal {Z}$
-stable ASH-algebra has generator rank one (see Theorem 5.10).
$\mathcal {Z}$
-stable ASH-algebra has generator rank one (see Theorem 5.10).
To compute the generator rank of a subhomogeneous
![]() $C^*\!$
-algebra, we use that it is a successive extension by homogeneous
$C^*\!$
-algebra, we use that it is a successive extension by homogeneous
![]() $C^*\!$
-algebras. Using the results from Section 4, we compute the generator rank of the homogeneous parts. The crucial extra ingredient is Proposition 5.3, which allows us to compute the generator rank of the extension by a homogeneous
$C^*\!$
-algebras. Using the results from Section 4, we compute the generator rank of the homogeneous parts. The crucial extra ingredient is Proposition 5.3, which allows us to compute the generator rank of the extension by a homogeneous
![]() $C^*\!$
-algebra.
$C^*\!$
-algebra.
Given a
![]() $C^*\!$
-algebra A, we equip the primitive ideal space
$C^*\!$
-algebra A, we equip the primitive ideal space
![]() $\operatorname {\mathrm {Prim}}(A)$
with the hull-kernel topology (see [Reference BlackadarBla06, Section II.6.5, p. 111ff] for details). Given an ideal
$\operatorname {\mathrm {Prim}}(A)$
with the hull-kernel topology (see [Reference BlackadarBla06, Section II.6.5, p. 111ff] for details). Given an ideal
![]() $I\subseteq A$
, the set
$I\subseteq A$
, the set
![]() $\operatorname {\mathrm {hull}}(I):=\{J\in \operatorname {\mathrm {Prim}}(A) : I\subseteq J\}$
is a closed subset of
$\operatorname {\mathrm {hull}}(I):=\{J\in \operatorname {\mathrm {Prim}}(A) : I\subseteq J\}$
is a closed subset of
![]() $\operatorname {\mathrm {Prim}}(A)$
, and this defines a natural bijection between ideals of A and closed subsets of
$\operatorname {\mathrm {Prim}}(A)$
, and this defines a natural bijection between ideals of A and closed subsets of
![]() $\operatorname {\mathrm {Prim}}(A)$
.
$\operatorname {\mathrm {Prim}}(A)$
.
Lemma 5.1 Let A be a unital
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals. Then, the following are equivalent:
$(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals. Then, the following are equivalent:
-
(1)
 $\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
.
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. -
(2) For each
 $\varphi \in A^*$
, we have
$\varphi \in A^*$
, we have
 $\lim _{k\to \infty }\|\varphi |_{I_k}\| = 0$
.
$\lim _{k\to \infty }\|\varphi |_{I_k}\| = 0$
.
Proof For each
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $z_k$
denote the support projection of
$z_k$
denote the support projection of
![]() $I_k$
in
$I_k$
in
![]() $A^{**}$
, and let
$A^{**}$
, and let
![]() $\pi _k\colon A\to A/I_k$
denote the quotient map.
$\pi _k\colon A\to A/I_k$
denote the quotient map.
Claim: Let
![]() $\varphi \in A^*_+$
and
$\varphi \in A^*_+$
and
![]() $k\in \mathbb {N}$
. Then,
$k\in \mathbb {N}$
. Then,
![]() $\|\varphi |_{I_k}\|=\varphi ^{**}(z_k)$
. To prove the claim, let
$\|\varphi |_{I_k}\|=\varphi ^{**}(z_k)$
. To prove the claim, let
![]() $(h_\alpha )_\alpha $
denote an increasing, positive, contractive approximate unit of
$(h_\alpha )_\alpha $
denote an increasing, positive, contractive approximate unit of
![]() $I_k$
. Since
$I_k$
. Since
![]() $\varphi |_{I_k}$
is a positive functional on
$\varphi |_{I_k}$
is a positive functional on
![]() $I_k$
, we have
$I_k$
, we have
![]() $\|\varphi |_{I_k}\| = \lim _\alpha \varphi (h_\alpha )$
by [Reference BlackadarBla06, Proposition II.6.2.5]. Using also that
$\|\varphi |_{I_k}\| = \lim _\alpha \varphi (h_\alpha )$
by [Reference BlackadarBla06, Proposition II.6.2.5]. Using also that
![]() $z_k$
is the weak*-limit of
$z_k$
is the weak*-limit of
![]() $(h_\alpha )_\alpha $
in
$(h_\alpha )_\alpha $
in
![]() $A^{**}$
, we get
$A^{**}$
, we get
which proves the claim.
Let
![]() $S(A)$
denote the set of states on A, which is a compact, convex subset of
$S(A)$
denote the set of states on A, which is a compact, convex subset of
![]() $A^*$
, and let
$A^*$
, and let
![]() $P(A)$
denote the pure states on A, which agrees with the set of extreme points in
$P(A)$
denote the pure states on A, which agrees with the set of extreme points in
![]() $S(A)$
. Given
$S(A)$
. Given
![]() $a\in (A^{**})_{\mathrm {sa}}$
, we let
$a\in (A^{**})_{\mathrm {sa}}$
, we let
![]() $\widehat {a}\colon S(A)\to \mathbb {R}$
be given by
$\widehat {a}\colon S(A)\to \mathbb {R}$
be given by
for
![]() $\varphi \in S(A)$
. Then,
$\varphi \in S(A)$
. Then,
![]() $\widehat {a}$
is affine. If
$\widehat {a}$
is affine. If
![]() $a\in A_{\mathrm {sa}}$
, then
$a\in A_{\mathrm {sa}}$
, then
![]() $\widehat {a}$
is continuous. Given
$\widehat {a}$
is continuous. Given
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $(h_\alpha )_\alpha $
be an increasing approximate unit of
$(h_\alpha )_\alpha $
be an increasing approximate unit of
![]() $I_k$
. Then,
$I_k$
. Then,
![]() $\widehat {z_k}$
is the pointwise supremum of the increasing net
$\widehat {z_k}$
is the pointwise supremum of the increasing net
![]() $(\widehat {h_\alpha })_\alpha $
of continuous functions, and therefore lower-semicontinuous.
$(\widehat {h_\alpha })_\alpha $
of continuous functions, and therefore lower-semicontinuous.
To show that (1) implies (2), assume that
![]() $\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Let
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Let
![]() $\varphi \in P(A)$
. Since every pure state on A factors through an irreducible representation, there exists k such that
$\varphi \in P(A)$
. Since every pure state on A factors through an irreducible representation, there exists k such that
![]() $\varphi $
factors through
$\varphi $
factors through
![]() $\pi _k$
. Let
$\pi _k$
. Let
![]() $\bar {\varphi }\in (A/I_k)^*$
such that
$\bar {\varphi }\in (A/I_k)^*$
such that
![]() $\varphi =\bar {\varphi }\circ \pi _k$
. We have
$\varphi =\bar {\varphi }\circ \pi _k$
. We have
![]() $\pi _k^{**}(z_k)=0$
, and therefore
$\pi _k^{**}(z_k)=0$
, and therefore
Thus,
![]() $(\widehat {z_k})_k$
is a decreasing sequence of lower semicontinuous, affine functions with
$(\widehat {z_k})_k$
is a decreasing sequence of lower semicontinuous, affine functions with
![]() $\lim _{k\to \infty }\widehat {z_k}(\varphi )=0$
for each
$\lim _{k\to \infty }\widehat {z_k}(\varphi )=0$
for each
![]() $\varphi \in P(A)$
. By [Reference AlfsenAlf71, Proposition 1.4.10, p. 36], we have
$\varphi \in P(A)$
. By [Reference AlfsenAlf71, Proposition 1.4.10, p. 36], we have
![]() $\lim _{k\to \infty }\widehat {z_k}(\varphi )=0$
for each
$\lim _{k\to \infty }\widehat {z_k}(\varphi )=0$
for each
![]() $\varphi \in S(A)$
. Applying the claim, it follows that
$\varphi \in S(A)$
. Applying the claim, it follows that
![]() $\lim _{k\to \infty }\|\varphi |_{I_k}\|=0$
for every
$\lim _{k\to \infty }\|\varphi |_{I_k}\|=0$
for every
![]() $\varphi \in S(A)$
. Now, (2) follows using that every functional in
$\varphi \in S(A)$
. Now, (2) follows using that every functional in
![]() $A^*$
is a linear combination of four states, by [Reference BlackadarBla06, Theorem II.6.3.4, p. 106].
$A^*$
is a linear combination of four states, by [Reference BlackadarBla06, Theorem II.6.3.4, p. 106].
To show that (2) implies (1), assume that
![]() $\bigcup _k \operatorname {\mathrm {hull}}(I_k)\neq \operatorname {\mathrm {Prim}}(A)$
. We will show that (2) does not hold. Let
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)\neq \operatorname {\mathrm {Prim}}(A)$
. We will show that (2) does not hold. Let
![]() $J\subseteq A$
be a primitive ideal with
$J\subseteq A$
be a primitive ideal with
![]() $J\notin \bigcup _k \operatorname {\mathrm {hull}}(I_k)$
, and let
$J\notin \bigcup _k \operatorname {\mathrm {hull}}(I_k)$
, and let
![]() $\bar {\varphi }$
be a pure state on
$\bar {\varphi }$
be a pure state on
![]() $A/J$
. Let
$A/J$
. Let
![]() $\pi \colon A\to A/J$
denote the quotient map. Set
$\pi \colon A\to A/J$
denote the quotient map. Set
![]() $\varphi :=\bar {\varphi }\circ \pi $
, which is a pure state on A. Let
$\varphi :=\bar {\varphi }\circ \pi $
, which is a pure state on A. Let
![]() $k\in \mathbb {N}$
. In general, the restriction of a pure state to an ideal is either zero or again a pure state. Since
$k\in \mathbb {N}$
. In general, the restriction of a pure state to an ideal is either zero or again a pure state. Since
![]() $J\notin \operatorname {\mathrm {hull}}(I_k)$
, we have
$J\notin \operatorname {\mathrm {hull}}(I_k)$
, we have
![]() $\varphi |_{I_k}\neq 0$
, and thus
$\varphi |_{I_k}\neq 0$
, and thus
![]() $\|\varphi |_{I_k}\|=1$
. Thus,
$\|\varphi |_{I_k}\|=1$
. Thus,
![]() $\lim _{k\to \infty }\|\varphi |_{I_k}\|=1 \neq 0$
.
$\lim _{k\to \infty }\|\varphi |_{I_k}\|=1 \neq 0$
.
Proposition 5.2 Let A be a
![]() $C^*\!$
-algebra, let
$C^*\!$
-algebra, let
![]() $(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals such that
$(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals such that
![]() $\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
, and let
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
, and let
![]() $B\subseteq A$
be a sub-
$B\subseteq A$
be a sub-
![]() $C^*\!$
-algebra. Assume that
$C^*\!$
-algebra. Assume that
![]() $B/(B\cap I_k)=A/I_k$
for each k. Then,
$B/(B\cap I_k)=A/I_k$
for each k. Then,
![]() $B=A$
.
$B=A$
.
Proof We first reduce to the unital case. So assume that A is nonunital, let
![]() $\widetilde {A}$
denote its minimal unitization, and let
$\widetilde {A}$
denote its minimal unitization, and let
![]() $\bar {B}$
denote the sub-
$\bar {B}$
denote the sub-
![]() $C^*\!$
-algebra of
$C^*\!$
-algebra of
![]() $\widetilde {A}$
generated by B and the unit of
$\widetilde {A}$
generated by B and the unit of
![]() $\widetilde {A}$
. For each
$\widetilde {A}$
. For each
![]() $k\in \mathbb {N}$
, we consider
$k\in \mathbb {N}$
, we consider
![]() $I_k$
as an ideal in
$I_k$
as an ideal in
![]() $\widetilde {A}$
. Let
$\widetilde {A}$
. Let
![]() $\pi _k\colon A\to A/I_k$
and
$\pi _k\colon A\to A/I_k$
and
![]() $\pi _k^+\colon \widetilde {A}\to \widetilde {A}/I_k$
denote the quotient maps. Note that
$\pi _k^+\colon \widetilde {A}\to \widetilde {A}/I_k$
denote the quotient maps. Note that
![]() $\widetilde {A}/I_k$
is naturally isomorphic to
$\widetilde {A}/I_k$
is naturally isomorphic to
![]() $(A/I_k)^+$
, the forced unitization of
$(A/I_k)^+$
, the forced unitization of
![]() $A/I_k$
. By assumption,
$A/I_k$
. By assumption,
![]() $\pi _k(B)=\pi _k(A)$
. It follows that
$\pi _k(B)=\pi _k(A)$
. It follows that
![]() $\pi _k^+(\bar {B})=\pi _k^+(\widetilde {A})$
. Furthermore,
$\pi _k^+(\bar {B})=\pi _k^+(\widetilde {A})$
. Furthermore,
![]() $\operatorname {\mathrm {Prim}}(\widetilde {A})$
is the union of the hulls of the
$\operatorname {\mathrm {Prim}}(\widetilde {A})$
is the union of the hulls of the
![]() $I_k$
. Then, assuming that the results holds in the unital case, we obtain
$I_k$
. Then, assuming that the results holds in the unital case, we obtain
![]() $\bar {B}=\widetilde {A}$
, which implies
$\bar {B}=\widetilde {A}$
, which implies
![]() $B\,{=}\,A$
.
$B\,{=}\,A$
.
Thus, we may assume from now on that A is unital. To reach a contradiction, assume that
![]() $B\neq A$
. Using Hahn–Banach, we choose
$B\neq A$
. Using Hahn–Banach, we choose
![]() $\varphi \in A^*$
with
$\varphi \in A^*$
with
![]() $\varphi |_{B}\equiv 0$
and
$\varphi |_{B}\equiv 0$
and
![]() $\|\varphi \|=1$
. Apply Lemma 5.1 to obtain k such that
$\|\varphi \|=1$
. Apply Lemma 5.1 to obtain k such that
![]() $\|\varphi |_{I_k}\|<\tfrac {1}{8}$
. Since every functional is a linear combination of four states [Reference BlackadarBla06, Theorem II.6.3.4, p.106], we obtain
$\|\varphi |_{I_k}\|<\tfrac {1}{8}$
. Since every functional is a linear combination of four states [Reference BlackadarBla06, Theorem II.6.3.4, p.106], we obtain
![]() $\psi _m\in (I_k)^*_+$
with
$\psi _m\in (I_k)^*_+$
with
![]() $\varphi |_{I_k}=\sum _{m=0}^3 i^m \psi _m$
, and we may also ensure that
$\varphi |_{I_k}=\sum _{m=0}^3 i^m \psi _m$
, and we may also ensure that
![]() $\|\psi _m\|\leq \|\varphi |_{I_k}\|<\tfrac {1}{8}$
. Using [Reference BlackadarBla06, Theorem II.6.4.16, p. 111], we can extend each
$\|\psi _m\|\leq \|\varphi |_{I_k}\|<\tfrac {1}{8}$
. Using [Reference BlackadarBla06, Theorem II.6.4.16, p. 111], we can extend each
![]() $\psi _m$
to a positive functional
$\psi _m$
to a positive functional
![]() $\tilde {\psi }_m\in A^*_+$
with
$\tilde {\psi }_m\in A^*_+$
with
![]() $\|\tilde {\psi }_m\|=\|\psi _m\|$
. Set
$\|\tilde {\psi }_m\|=\|\psi _m\|$
. Set
![]() $\omega :=\varphi -\sum _{m=0}^3 i^m \tilde {\psi }_m$
. Then,
$\omega :=\varphi -\sum _{m=0}^3 i^m \tilde {\psi }_m$
. Then,
![]() $\omega \in A^*$
satisfies
$\omega \in A^*$
satisfies
![]() $\omega |_{I_k}\equiv 0$
and
$\omega |_{I_k}\equiv 0$
and
![]() ${\|\varphi -\omega \|<\tfrac {1}{2}}$
.
${\|\varphi -\omega \|<\tfrac {1}{2}}$
.
Let
![]() $\bar {\omega }\in (A/I_k)^*$
satisfy
$\bar {\omega }\in (A/I_k)^*$
satisfy
![]() $\omega =\bar {\omega }\circ \pi _k$
. Given
$\omega =\bar {\omega }\circ \pi _k$
. Given
![]() $a\in A$
, use that
$a\in A$
, use that
![]() $A/I_k=\pi _k(B)$
to choose
$A/I_k=\pi _k(B)$
to choose
![]() $b\in B$
with
$b\in B$
with
![]() $\pi _k(b)=\pi _k(a)$
and
$\pi _k(b)=\pi _k(a)$
and
![]() $\|b\|=\|\pi _k(a)\|$
(see [Reference BlackadarBla06, Proposition II.5.1.5]). Then,
$\|b\|=\|\pi _k(a)\|$
(see [Reference BlackadarBla06, Proposition II.5.1.5]). Then,
![]() $\omega (a)=\omega (b)$
, and thus
$\omega (a)=\omega (b)$
, and thus
Hence,
![]() $\|\omega \|\leq \tfrac {1}{2}$
, and so
$\|\omega \|\leq \tfrac {1}{2}$
, and so
![]() $1=\|\varphi \|\leq \|\varphi -\omega \|+\|\omega \|<1$
, which is a contradiction.
$1=\|\varphi \|\leq \|\varphi -\omega \|+\|\omega \|<1$
, which is a contradiction.
Proposition 5.3 Let A be a separable
![]() $C^*\!$
-algebra, and let
$C^*\!$
-algebra, and let
![]() $(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals satisfying
$(I_k)_{k\in \mathbb {N}}$
be a decreasing sequence of ideals satisfying
![]() $\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Then,
$\bigcup _k \operatorname {\mathrm {hull}}(I_k)=\operatorname {\mathrm {Prim}}(A)$
. Then,
Proof
Part 1: We verify the equality for
![]() $\operatorname {\mathrm {gr}}_0$
. For each k, set
$\operatorname {\mathrm {gr}}_0$
. For each k, set
![]() $B_k:=A/I_k$
and let
$B_k:=A/I_k$
and let
![]() $\pi _k\colon A\to B_k$
denote the quotient map. By Theorem 2.5, we have
$\pi _k\colon A\to B_k$
denote the quotient map. By Theorem 2.5, we have
![]() $\operatorname {\mathrm {gr}}_0(A)\geq \operatorname {\mathrm {gr}}_0(B_k)$
. It thus remains to prove
$\operatorname {\mathrm {gr}}_0(A)\geq \operatorname {\mathrm {gr}}_0(B_k)$
. It thus remains to prove
![]() $\operatorname {\mathrm {gr}}_0(A) \leq \sup _k \operatorname {\mathrm {gr}}_0(B_k)$
. Set
$\operatorname {\mathrm {gr}}_0(A) \leq \sup _k \operatorname {\mathrm {gr}}_0(B_k)$
. Set
![]() $n:=\sup _k \operatorname {\mathrm {gr}}_0(B_k)$
, which we may assume to be finite. For each k, set
$n:=\sup _k \operatorname {\mathrm {gr}}_0(B_k)$
, which we may assume to be finite. For each k, set
Since
![]() $\operatorname {\mathrm {gr}}_0(B_k)\leq n$
, and since
$\operatorname {\mathrm {gr}}_0(B_k)\leq n$
, and since
![]() $B_k$
is separable,
$B_k$
is separable,
![]() $\operatorname {\mathrm {Gen}}_{n+1}(B_k)_{\mathrm {sa}}$
is a dense
$\operatorname {\mathrm {Gen}}_{n+1}(B_k)_{\mathrm {sa}}$
is a dense
![]() $G_\delta $
-subset of
$G_\delta $
-subset of
![]() $(B_k)^{n+1}_{\mathrm {sa}}$
by Theorem 2.2. We deduce that
$(B_k)^{n+1}_{\mathrm {sa}}$
by Theorem 2.2. We deduce that
![]() $D_k$
is a dense
$D_k$
is a dense
![]() $G_\delta $
-subset of
$G_\delta $
-subset of
![]() $A^{n+1}_{\mathrm {sa}}$
. Then, by the Baire category theorem,
$A^{n+1}_{\mathrm {sa}}$
. Then, by the Baire category theorem,
![]() $D:=\bigcap _k D_k$
is a dense subset of
$D:=\bigcap _k D_k$
is a dense subset of
![]() $A^{n+1}_{\mathrm {sa}}$
.
$A^{n+1}_{\mathrm {sa}}$
.
Let us show that
![]() $D\subseteq \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
, which will imply that
$D\subseteq \operatorname {\mathrm {Gen}}_{n+1}(A)_{\mathrm {sa}}$
, which will imply that
![]() $\operatorname {\mathrm {gr}}_0(A)\leq n$
. Let
$\operatorname {\mathrm {gr}}_0(A)\leq n$
. Let
![]() $\mathbf {a}\in D$
, and set
$\mathbf {a}\in D$
, and set
![]() $B:=C^*(\mathbf {a})\subseteq A$
. By construction, we have
$B:=C^*(\mathbf {a})\subseteq A$
. By construction, we have
![]() $\pi _k(B)=A/I_k$
for each k. Applying Proposition 5.2, we get
$\pi _k(B)=A/I_k$
for each k. Applying Proposition 5.2, we get
![]() $B=A$
, and thus
$B=A$
, and thus
![]() $\mathbf {a}\in \operatorname {\mathrm {Gen}}_{k}(A)_{\mathrm {sa}}$
.
$\mathbf {a}\in \operatorname {\mathrm {Gen}}_{k}(A)_{\mathrm {sa}}$
.
Part 2: We verify the equality for
![]() $\operatorname {\mathrm {gr}}$
. If A is unital, this follows from Part 1. So assume that A is nonunital. We consider
$\operatorname {\mathrm {gr}}$
. If A is unital, this follows from Part 1. So assume that A is nonunital. We consider
![]() $I_k$
as an ideal in
$I_k$
as an ideal in
![]() $\widetilde {A}$
. As in the proof of Proposition 5.2, we see that
$\widetilde {A}$
. As in the proof of Proposition 5.2, we see that
![]() $\widetilde {A}/I_k\cong (A/I_k)^+$
, and that
$\widetilde {A}/I_k\cong (A/I_k)^+$
, and that
![]() $\operatorname {\mathrm {Prim}}(\widetilde {A})$
is the union of the hulls of the
$\operatorname {\mathrm {Prim}}(\widetilde {A})$
is the union of the hulls of the
![]() $I_k$
. By [Reference Thiel and WinterThi21, Lemma 6.1], we have
$I_k$
. By [Reference Thiel and WinterThi21, Lemma 6.1], we have
![]() $\operatorname {\mathrm {gr}}(B)=\operatorname {\mathrm {gr}}(B^+)$
for every
$\operatorname {\mathrm {gr}}(B)=\operatorname {\mathrm {gr}}(B^+)$
for every
![]() $C^*\!$
-algebra B. Applying Part 1 at the second step, we get
$C^*\!$
-algebra B. Applying Part 1 at the second step, we get
Lemma 5.4 Let A and B be separable
![]() $C^*\!$
-algebras. Assume that no nonzero quotient of A is isomorphic to a quotient of B. Then,
$C^*\!$
-algebras. Assume that no nonzero quotient of A is isomorphic to a quotient of B. Then,
Proof The equality for
![]() $\operatorname {\mathrm {gr}}_0$
follows directly from [Reference Thiel and WinterThi21, Proposition 5.10] by considering the ideal
$\operatorname {\mathrm {gr}}_0$
follows directly from [Reference Thiel and WinterThi21, Proposition 5.10] by considering the ideal
![]() $I:=A$
. Applying Proposition 2.4 at the first and last steps, and using the formula for
$I:=A$
. Applying Proposition 2.4 at the first and last steps, and using the formula for
![]() $\operatorname {\mathrm {gr}}_0$
and that
$\operatorname {\mathrm {gr}}_0$
and that
![]() $\operatorname {\mathrm {rr}}(A\oplus B)=\max \{\operatorname {\mathrm {rr}}(A),\operatorname {\mathrm {rr}}(B)\}$
at the second step, we get
$\operatorname {\mathrm {rr}}(A\oplus B)=\max \{\operatorname {\mathrm {rr}}(A),\operatorname {\mathrm {rr}}(B)\}$
at the second step, we get
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A\oplus B) &= \max \big\{ \operatorname{\mathrm{gr}}_0(A\oplus B), \operatorname{\mathrm{rr}}(A\oplus B) \big\} \\ &= \max \big\{ \operatorname{\mathrm{gr}}_0(A), \operatorname{\mathrm{gr}}_0(B), \operatorname{\mathrm{rr}}(A), \operatorname{\mathrm{rr}}(B) \big\} = \max \big\{ \operatorname{\mathrm{gr}}(A), \operatorname{\mathrm{gr}}(B) \big\}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A\oplus B) &= \max \big\{ \operatorname{\mathrm{gr}}_0(A\oplus B), \operatorname{\mathrm{rr}}(A\oplus B) \big\} \\ &= \max \big\{ \operatorname{\mathrm{gr}}_0(A), \operatorname{\mathrm{gr}}_0(B), \operatorname{\mathrm{rr}}(A), \operatorname{\mathrm{rr}}(B) \big\} = \max \big\{ \operatorname{\mathrm{gr}}(A), \operatorname{\mathrm{gr}}(B) \big\}.\\[-34pt] \end{align*} $$
Theorem 5.5 Let A be a subhomogeneous
![]() $C^*\!$
-algebra. For each
$C^*\!$
-algebra. For each
![]() $d\geq 1$
, set
$d\geq 1$
, set
![]() $X_d:=\operatorname {\mathrm {Prim}}_d(A)$
, the subset of the primitive ideal space of A corresponding to d-dimensional irreducible representations. Then,
$X_d:=\operatorname {\mathrm {Prim}}_d(A)$
, the subset of the primitive ideal space of A corresponding to d-dimensional irreducible representations. Then,
 $$ \begin{align*} \operatorname{\mathrm{gr}}_0(A) = \operatorname{\mathrm{gr}}(A) &= \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \max_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}_0(A) = \operatorname{\mathrm{gr}}(A) &= \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \max_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*} $$
Proof By Proposition 2.4, we have
![]() $\operatorname {\mathrm {gr}}_0(A)\leq \operatorname {\mathrm {gr}}(A)$
. Given
$\operatorname {\mathrm {gr}}_0(A)\leq \operatorname {\mathrm {gr}}(A)$
. Given
![]() $d\geq 1$
, let
$d\geq 1$
, let
![]() $A_d$
denote the ideal quotient of A corresponding to the locally closed set
$A_d$
denote the ideal quotient of A corresponding to the locally closed set
![]() $\operatorname {\mathrm {Prim}}_d(A)\subseteq \operatorname {\mathrm {Prim}}(A)$
. Applying Theorem 2.5, we obtain
$\operatorname {\mathrm {Prim}}_d(A)\subseteq \operatorname {\mathrm {Prim}}(A)$
. Applying Theorem 2.5, we obtain
![]() $\operatorname {\mathrm {gr}}_0(A_d) \leq \operatorname {\mathrm {gr}}_0(A)$
. Note that
$\operatorname {\mathrm {gr}}_0(A_d) \leq \operatorname {\mathrm {gr}}_0(A)$
. Note that
![]() $A_d$
is d-homogeneous. In particular,
$A_d$
is d-homogeneous. In particular,
![]() $A_1\cong C_0(X_1)$
. Using Theorem 2.7, we get
$A_1\cong C_0(X_1)$
. Using Theorem 2.7, we get
For
![]() $d\geq 2$
, applying Theorem 4.17, we get
$d\geq 2$
, applying Theorem 4.17, we get
 $$\begin{align*}\left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil = \operatorname{\mathrm{gr}}_0(A_d) \leq \operatorname{\mathrm{gr}}_0(A). \end{align*}$$
$$\begin{align*}\left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil = \operatorname{\mathrm{gr}}_0(A_d) \leq \operatorname{\mathrm{gr}}_0(A). \end{align*}$$
It remains to verify that
 $$ \begin{align} \operatorname{\mathrm{gr}}(A) \leq \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \sup_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{gr}}(A) \leq \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \sup_{d\geq 2} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align} $$
Recall that a
![]() $C^*\!$
-algebra is m-subhomogeneous if each of its irreducible representations has dimension at most m. We prove the inequality (5.1) by induction over m. Note that
$C^*\!$
-algebra is m-subhomogeneous if each of its irreducible representations has dimension at most m. We prove the inequality (5.1) by induction over m. Note that
![]() $1$
-subhomogeneous
$1$
-subhomogeneous
![]() $C^*\!$
-algebras are precisely commutative
$C^*\!$
-algebras are precisely commutative
![]() $C^*\!$
-algebras, in which case (5.1) follows from Theorem 2.7.
$C^*\!$
-algebras, in which case (5.1) follows from Theorem 2.7.
Let
![]() $m\geq 2$
, assume that (5.1) holds for
$m\geq 2$
, assume that (5.1) holds for
![]() $(m-1)$
-subhomogeneous
$(m-1)$
-subhomogeneous
![]() $C^*\!$
-algebras, and assume that A is m-subhomogeneous. Let I be the ideal of A corresponding to the open subset
$C^*\!$
-algebras, and assume that A is m-subhomogeneous. Let I be the ideal of A corresponding to the open subset
![]() $X_m\subseteq \operatorname {\mathrm {Prim}}(A)$
. Note that
$X_m\subseteq \operatorname {\mathrm {Prim}}(A)$
. Note that
![]() $A/I$
is
$A/I$
is
![]() $(m-1)$
-subhomogeneous. Set
$(m-1)$
-subhomogeneous. Set
 $$\begin{align*}n := \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \sup_{d=1,\ldots,m-1} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*}$$
$$\begin{align*}n := \max\left\{ \operatorname{\mathrm{locdim}}(X_1\times X_1), \sup_{d=1,\ldots,m-1} \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_d)+1}{2d-2}\right\rceil \right\}. \end{align*}$$
By assumption of the induction, we have
![]() $\operatorname {\mathrm {gr}}(A/I)\leq n$
. We need to prove that
$\operatorname {\mathrm {gr}}(A/I)\leq n$
. We need to prove that
 $$\begin{align*}\operatorname{\mathrm{gr}}(A)\leq\max\left\{ n, \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_m)+1}{2m-2}\right\rceil \right\}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gr}}(A)\leq\max\left\{ n, \left\lceil\frac{\operatorname{\mathrm{locdim}}(X_m)+1}{2m-2}\right\rceil \right\}. \end{align*}$$
Set
![]() $l := \operatorname {\mathrm {locdim}}(X_m)$
and
$l := \operatorname {\mathrm {locdim}}(X_m)$
and
 $$ \begin{align*} \mathcal{S}_1 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : \operatorname{\mathrm{gr}}(B/(B\cap I))\leq n \big\}, \quad\text{ and }\quad \\ \mathcal{S}_2 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : B\cap I\ m\text{-homogeneous}, \operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(B\cap I))\leq l \big\}. \end{align*} $$
$$ \begin{align*} \mathcal{S}_1 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : \operatorname{\mathrm{gr}}(B/(B\cap I))\leq n \big\}, \quad\text{ and }\quad \\ \mathcal{S}_2 &:= \big\{ B\in\operatorname{\mathrm{Sub}}_{\mathrm{sep}}(A) : B\cap I\ m\text{-homogeneous}, \operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(B\cap I))\leq l \big\}. \end{align*} $$
As noted in Paragraph 3.1, the collection
![]() $\{D\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A/I) : \operatorname {\mathrm {gr}}(D)\leq n\}$
is
$\{D\in \operatorname {\mathrm {Sub}}_{\mathrm {sep}}(A/I) : \operatorname {\mathrm {gr}}(D)\leq n\}$
is
![]() $\sigma $
-complete and cofinal. Applying Lemma 3.2(2), we obtain that
$\sigma $
-complete and cofinal. Applying Lemma 3.2(2), we obtain that
![]() $\mathcal {S}_1$
is
$\mathcal {S}_1$
is
![]() $\sigma $
-complete and cofinal. Similarly, using Proposition 3.5 and Lemma 3.2(1), we see that
$\sigma $
-complete and cofinal. Similarly, using Proposition 3.5 and Lemma 3.2(1), we see that
![]() $\mathcal {S}_2$
is
$\mathcal {S}_2$
is
![]() $\sigma $
-complete and cofinal. Hence,
$\sigma $
-complete and cofinal. Hence,
![]() $\mathcal {S}_1\cap \mathcal {S}_2$
is
$\mathcal {S}_1\cap \mathcal {S}_2$
is
![]() $\sigma $
-complete and cofinal as well. Using Theorem 2.6, and using that A is approximated by
$\sigma $
-complete and cofinal as well. Using Theorem 2.6, and using that A is approximated by
![]() $\mathcal {S}_1\cap \mathcal {S}_2$
, it suffices to verify that every
$\mathcal {S}_1\cap \mathcal {S}_2$
, it suffices to verify that every
![]() $B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
$B\in \mathcal {S}_1\cap \mathcal {S}_2$
satisfies
Let
![]() $B\in \mathcal {S}_1\cap \mathcal {S}_2$
. Set
$B\in \mathcal {S}_1\cap \mathcal {S}_2$
. Set
![]() $J:=B\cap I$
. By construction, J is m-homogeneous with
$J:=B\cap I$
. By construction, J is m-homogeneous with
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(J))\leq l$
, and
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(J))\leq l$
, and
![]() $B/J$
is
$B/J$
is
![]() $(m-1)$
-subhomogeneous with
$(m-1)$
-subhomogeneous with
![]() $\operatorname {\mathrm {gr}}(B/J)\leq n$
. Note that J is the ideal of B corresponding to
$\operatorname {\mathrm {gr}}(B/J)\leq n$
. Note that J is the ideal of B corresponding to
![]() $\operatorname {\mathrm {Prim}}_m(B)$
. Since B is separable,
$\operatorname {\mathrm {Prim}}_m(B)$
. Since B is separable,
![]() $\operatorname {\mathrm {Prim}}_m(B)$
is
$\operatorname {\mathrm {Prim}}_m(B)$
is
![]() $\sigma $
-compact. Choose an increasing sequence
$\sigma $
-compact. Choose an increasing sequence
![]() $(Y_k)_{k\in \mathbb {N}}$
of compact subsets of
$(Y_k)_{k\in \mathbb {N}}$
of compact subsets of
![]() $\operatorname {\mathrm {Prim}}_m(B)$
such that
$\operatorname {\mathrm {Prim}}_m(B)$
such that
![]() $\operatorname {\mathrm {Prim}}_m(B)=\bigcup _k Y_k$
.
$\operatorname {\mathrm {Prim}}_m(B)=\bigcup _k Y_k$
.
For each k, note that
![]() $Y_k\subseteq \operatorname {\mathrm {Prim}}_m(B)$
is closed, and let
$Y_k\subseteq \operatorname {\mathrm {Prim}}_m(B)$
is closed, and let
![]() $J_k$
be the ideal of J corresponding to the open subset
$J_k$
be the ideal of J corresponding to the open subset
![]() $\operatorname {\mathrm {Prim}}_m(B)\setminus Y_k$
. Considering
$\operatorname {\mathrm {Prim}}_m(B)\setminus Y_k$
. Considering
![]() $J_k$
as an ideal of B, we have
$J_k$
as an ideal of B, we have
![]() $B/J_k\cong (J/J_k) \oplus B/J$
. Since
$B/J_k\cong (J/J_k) \oplus B/J$
. Since
![]() $J/J_k$
is m-homogeneous, and
$J/J_k$
is m-homogeneous, and
![]() $B/J$
is
$B/J$
is
![]() $(m-1)$
-subhomogeneous, no nonzero quotient of
$(m-1)$
-subhomogeneous, no nonzero quotient of
![]() $J/J_k$
is isomorphic to a quotient of
$J/J_k$
is isomorphic to a quotient of
![]() $B/J$
. Applying Lemma 5.4, we obtain
$B/J$
. Applying Lemma 5.4, we obtain
Since
![]() $J/J_k$
is a quotient of J, and J is m-homogeneous with
$J/J_k$
is a quotient of J, and J is m-homogeneous with
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(J))\leq l$
, it follows from Theorems 2.5 and 4.17 that
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}(J))\leq l$
, it follows from Theorems 2.5 and 4.17 that
 $$\begin{align*}\operatorname{\mathrm{gr}}(J/J_k) \leq \operatorname{\mathrm{gr}}(J) = \left\lceil\frac{\operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(J))+1}{2m-2}\right\rceil \leq \left\lceil\frac{l+1}{2m-2}\right\rceil. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{gr}}(J/J_k) \leq \operatorname{\mathrm{gr}}(J) = \left\lceil\frac{\operatorname{\mathrm{locdim}}(\operatorname{\mathrm{Prim}}(J))+1}{2m-2}\right\rceil \leq \left\lceil\frac{l+1}{2m-2}\right\rceil. \end{align*}$$
Applying Proposition 5.3 at the first step, we obtain
as desired.
Remark 5.6 Let A be an m-subhomogeneous
![]() $C^*\!$
-algebra. For
$C^*\!$
-algebra. For
![]() $d=1,\ldots ,m$
, let
$d=1,\ldots ,m$
, let
![]() $A_d$
be the ideal quotient of A corresponding to the locally closed subset
$A_d$
be the ideal quotient of A corresponding to the locally closed subset
![]() $\operatorname {\mathrm {Prim}}_d(A)$
. Then, it follows from Theorem 5.5 that
$\operatorname {\mathrm {Prim}}_d(A)$
. Then, it follows from Theorem 5.5 that
Analogous formulas hold for the real and stable rank (see [Reference BrownBro16, Lemma 3.4]).
Corollary 5.7 Let A and B be subhomogeneous
![]() $C^*\!$
-algebras. Then,
$C^*\!$
-algebras. Then,
Proof Let
![]() $m\geq 1$
be such that A and B are m-subhomogeneous. Let
$m\geq 1$
be such that A and B are m-subhomogeneous. Let
![]() $A_d$
be the ideal quotient of A corresponding to
$A_d$
be the ideal quotient of A corresponding to
![]() $\operatorname {\mathrm {Prim}}_d(A)$
, and analogous for
$\operatorname {\mathrm {Prim}}_d(A)$
, and analogous for
![]() $B_d$
, for
$B_d$
, for
![]() $d=1,\ldots ,m$
. Then,
$d=1,\ldots ,m$
. Then,
![]() $A_d$
and
$A_d$
and
![]() $B_d$
are d-homogeneous, and
$B_d$
are d-homogeneous, and
![]() $A_d\oplus B_d$
is naturally isomorphic to the ideal quotient of
$A_d\oplus B_d$
is naturally isomorphic to the ideal quotient of
![]() $A\oplus B$
corresponding to
$A\oplus B$
corresponding to
![]() $\operatorname {\mathrm {Prim}}_d(A\oplus B)$
. Applying Theorem 5.5 (see also Remark 5.6) at the first and last steps, and using Lemma 4.18 at the second step, we get
$\operatorname {\mathrm {Prim}}_d(A\oplus B)$
. Applying Theorem 5.5 (see also Remark 5.6) at the first and last steps, and using Lemma 4.18 at the second step, we get
 $$ \begin{align*} \operatorname{\mathrm{gr}}(A \oplus B) &= \max_{d=1,\ldots,m} \operatorname{\mathrm{gr}}(A_d\oplus B_d) = \max_{d=1,\ldots,m} \max\big\{ \operatorname{\mathrm{gr}}(A_d),\operatorname{\mathrm{gr}}(B_d) \big\} \\ &= \max\left\{ \max_{d=1,\ldots,m}\operatorname{\mathrm{gr}}(A_d),\max_{d=1,\ldots,m}\operatorname{\mathrm{gr}}(B_d) \right\} = \max\big\{ \operatorname{\mathrm{gr}}(A), \operatorname{\mathrm{gr}}(B) \big\}. \\[-39pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{gr}}(A \oplus B) &= \max_{d=1,\ldots,m} \operatorname{\mathrm{gr}}(A_d\oplus B_d) = \max_{d=1,\ldots,m} \max\big\{ \operatorname{\mathrm{gr}}(A_d),\operatorname{\mathrm{gr}}(B_d) \big\} \\ &= \max\left\{ \max_{d=1,\ldots,m}\operatorname{\mathrm{gr}}(A_d),\max_{d=1,\ldots,m}\operatorname{\mathrm{gr}}(B_d) \right\} = \max\big\{ \operatorname{\mathrm{gr}}(A), \operatorname{\mathrm{gr}}(B) \big\}. \\[-39pt] \end{align*} $$
It is natural to expect that the generator rank of a direct sum of
![]() $C^*\!$
-algebras is the maximum of the generator ranks of the summands. The next result shows that this is the case if one of the summands is subhomogeneous. In general, however, this is unclear (see [Reference Thiel and WinterThi21, Questions 2.12 and 6.4]).
$C^*\!$
-algebras is the maximum of the generator ranks of the summands. The next result shows that this is the case if one of the summands is subhomogeneous. In general, however, this is unclear (see [Reference Thiel and WinterThi21, Questions 2.12 and 6.4]).
Proposition 5.8 Let A and B be
![]() $C^*\!$
-algebra,s and assume that B is subhomogeneous. Then,
$C^*\!$
-algebra,s and assume that B is subhomogeneous. Then,
Proof Let
![]() $m\geq 1$
such that B is m-subhomogeneous. The proof proceeds analogous to that of [Reference Thiel and WinterThi21, Proposition 5.12] (which is the result for
$m\geq 1$
such that B is m-subhomogeneous. The proof proceeds analogous to that of [Reference Thiel and WinterThi21, Proposition 5.12] (which is the result for
![]() $m=1$
) by considering the smallest ideal
$m=1$
) by considering the smallest ideal
![]() $I\subseteq A$
such that
$I\subseteq A$
such that
![]() $A/I$
is m-subhomogeneous (instead of the smallest I such that
$A/I$
is m-subhomogeneous (instead of the smallest I such that
![]() $A/I$
is commutative), and by using Corollary 5.7 instead of [Reference Thiel and WinterThi21, Proposition 5.9].
$A/I$
is commutative), and by using Corollary 5.7 instead of [Reference Thiel and WinterThi21, Proposition 5.9].
Lemma 5.9 Let A be a nonzero, subhomogeneous
![]() $C^*\!$
-algebra. Then,
$C^*\!$
-algebra. Then,
![]() $\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})=1$
.
$\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})=1$
.
Proof Given a finite subset
![]() $F\subseteq A$
, set
$F\subseteq A$
, set
![]() $A_F:=C^*(F)\subseteq A$
. Then,
$A_F:=C^*(F)\subseteq A$
. Then,
![]() $A_F$
is a finitely generated, subhomogeneous
$A_F$
is a finitely generated, subhomogeneous
![]() $C^*\!$
-algebra. By [Reference PearsNW06, Theorem 1.5], there is
$C^*\!$
-algebra. By [Reference PearsNW06, Theorem 1.5], there is
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}_d(A_F))\leq k$
for every
$\operatorname {\mathrm {locdim}}(\operatorname {\mathrm {Prim}}_d(A_F))\leq k$
for every
![]() $d\geq 1$
. For
$d\geq 1$
. For
![]() $p,q\in \mathbb {N}$
, let
$p,q\in \mathbb {N}$
, let
![]() $Z_{p,q}$
denote the dimension-drop algebra
$Z_{p,q}$
denote the dimension-drop algebra
For p and q sufficiently large (for example,
![]() $p,q\geq k+2$
), it follows from Theorem 5.5 that
$p,q\geq k+2$
), it follows from Theorem 5.5 that
![]() $\operatorname {\mathrm {gr}}(A_F\otimes Z_{p,q})\leq 1$
. Using that
$\operatorname {\mathrm {gr}}(A_F\otimes Z_{p,q})\leq 1$
. Using that
![]() $\mathcal {Z}$
is an inductive limit of dimension-drop algebras
$\mathcal {Z}$
is an inductive limit of dimension-drop algebras
![]() $Z_{p_n,q_n}$
with
$Z_{p_n,q_n}$
with
![]() $\lim _n p_n = \lim _n q_n =\infty $
, we have
$\lim _n p_n = \lim _n q_n =\infty $
, we have
![]() $\operatorname {\mathrm {gr}}(A_F\otimes \mathcal {Z})\leq 1$
by Theorem 2.6. The family of sub-
$\operatorname {\mathrm {gr}}(A_F\otimes \mathcal {Z})\leq 1$
by Theorem 2.6. The family of sub-
![]() $C^*\!$
-algebras
$C^*\!$
-algebras
![]() $A_F\otimes \mathcal {Z}\subseteq A\otimes \mathcal {Z}$
, indexed over the finite subsets of A ordered by inclusion, approximates
$A_F\otimes \mathcal {Z}\subseteq A\otimes \mathcal {Z}$
, indexed over the finite subsets of A ordered by inclusion, approximates
![]() $A\otimes \mathcal {Z}$
, whence
$A\otimes \mathcal {Z}$
, whence
![]() $\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})\leq 1$
by Theorem 2.6.
$\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})\leq 1$
by Theorem 2.6.
By [Reference Thiel and WinterThi21, Proposition 5.7], every noncommutative
![]() $C^*\!$
-algebra has generator rank at least one, and thus
$C^*\!$
-algebra has generator rank at least one, and thus
![]() $\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})=1$
.
$\operatorname {\mathrm {gr}}(A\otimes \mathcal {Z})=1$
.
Theorem 5.10 Every nonzero,
![]() $\mathcal {Z}$
-stable ASH-algebra has generator rank one.
$\mathcal {Z}$
-stable ASH-algebra has generator rank one.
If A is a separable,
![]() $\mathcal {Z}$
-stable ASH-algebra, then a generic element of A is a generator.
$\mathcal {Z}$
-stable ASH-algebra, then a generic element of A is a generator.
Proof Let A be a nonzero,
![]() $\mathcal {Z}$
-stable ASH-algebra. Let
$\mathcal {Z}$
-stable ASH-algebra. Let
![]() $(A_\lambda )_\lambda $
be an inductive system of subhomogeneous
$(A_\lambda )_\lambda $
be an inductive system of subhomogeneous
![]() $C^*\!$
-algebras such that
$C^*\!$
-algebras such that
![]() $A\cong \varinjlim _\lambda A_\lambda $
. Then,
$A\cong \varinjlim _\lambda A_\lambda $
. Then,
By Lemma 5.9, we have
![]() $\operatorname {\mathrm {gr}}(A_\lambda \otimes \mathcal {Z})\leq 1$
for each
$\operatorname {\mathrm {gr}}(A_\lambda \otimes \mathcal {Z})\leq 1$
for each
![]() $\lambda $
. Using Theorem 2.6, we get
$\lambda $
. Using Theorem 2.6, we get
![]() ${\operatorname {\mathrm {gr}}(A)\leq 1}$
. Since A is noncommutative, we deduce that
${\operatorname {\mathrm {gr}}(A)\leq 1}$
. Since A is noncommutative, we deduce that
![]() $\operatorname {\mathrm {gr}}(A)=1$
by [Reference Thiel and WinterThi21, Proposition 5.7].
$\operatorname {\mathrm {gr}}(A)=1$
by [Reference Thiel and WinterThi21, Proposition 5.7].
If A is also separable, then the generators in A form a dense
![]() $G_\delta $
-subset (see Remark 2.3).
$G_\delta $
-subset (see Remark 2.3).
Remark 5.11 Let A be a unital, separable,
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra. It was shown in [Reference Tikuisis, White and WinterTW14, Theorem 3.8] that A contains a generator. If A is also approximately subhomogeneous, then Theorem 5.10 shows that generators are even dense in A. I expect that every
$C^*\!$
-algebra. It was shown in [Reference Tikuisis, White and WinterTW14, Theorem 3.8] that A contains a generator. If A is also approximately subhomogeneous, then Theorem 5.10 shows that generators are even dense in A. I expect that every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra has generator rank one. However, in general, we do not even know that every
$C^*\!$
-algebra has generator rank one. However, in general, we do not even know that every
![]() $\mathcal {Z}$
-stable
$\mathcal {Z}$
-stable
![]() $C^*\!$
-algebra has real rank at most one.
$C^*\!$
-algebra has real rank at most one.
Acknowledgment
I want to thank the anonymous referee for his thorough reading of a former version of this work and for providing detailed feedback that helped greatly to improve the paper.