Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T18:21:00.493Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of Infinitely Presented Small Cancellation Groups and Quasi-homomorphisms

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  09 January 2019

Goulnara Arzhantseva  and
Cornelia Druţu
Goulnara Arzhantseva
Affiliation:
University of Vienna, Faculty of Mathematics, Oskar-Morgenstern-Platz 1, 1090 Vienna, Austria Email: goulnara.arzhantseva@univie.ac.at
Cornelia Druţu
Affiliation:
Mathematical Institute, AWB, Radcliffe Observatory Quarter, Woodstock Road, Oxford OX2 6GG, United Kingdom Email: drutu@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the geometry of infinitely presented groups satisfying the small cancellation condition 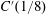$C^{\prime }(1/8)$, and introduce a standard decomposition (called the criss-cross decomposition) for the elements of such groups. Our method yields a direct construction of a linearly independent set of power continuum in the kernel of the comparison map between the bounded and the usual group cohomology in degree 2, without the use of free subgroups and extensions.

Keywords

small cancellation theoryGreendlinger lemmaquasi-homomorphismbounded cohomology

MSC classification

Primary: 20F06: Cancellation theory; application of van Kampen diagrams
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 997 - 1018
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported in part by the ERC grant ANALYTIC no. 259527, and by the Swiss NSF, under Sinergia grant CRSI22-130435. The second author was supported in part by the EPSRC grant no. EP/K032208/1 entitled “Geometric and analytic aspects of infinite groups”, by the project ANR Blanc ANR-10-BLAN 0116, acronym GGAA, and by the LABEX CEMPI.

References

Bavard, C., Longueur stable des commutateurs . Enseign. Math. (2) 37(1991), no. 1–2, 109–150.Google Scholar
Bestvina, M. and Fujiwara, K., Bounded cohomology of subgroups of mapping class groups . Geom. Topol. 6(2002), 69–89 (electronic). https://doi.org/10.2140/gt.2002.6.69.Google Scholar
Burger, M. and Monod, N., Bounded cohomology of lattices in higher rank Lie groups . J. Eur. Math. Soc. (JEMS) 1(1999), no. 2, 199–235. https://doi.org/10.1007/s100970050007.Google Scholar
Burger, M. and Monod, N., Continuous bounded cohomology and applications to rigidity theory . Geom. Funct. Anal. 12(2002), no. 2, 219–280. https://doi.org/10.1007/s00039-002-8245-9.Google Scholar
Brooks, R., Some remarks on bounded cohomology, Riemann surfaces and related topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978), Ann. of Math. Stud., vol. 97, Princeton Univ. Press, Princeton, N.J., 1981, pp. 53–63.Google Scholar
Dahmani, F., Guirardel, V., and Osin, D., Hyperbolically embedded subgroups and rotating families in groups acting on hyperbolic spaces . Mem. Amer. Math. Soc. 245(2017), no. 1156. https://doi.org/10.1090/memo/1156.Google Scholar
Epstein, D. B. A. and Fujiwara, K., The second bounded cohomology of word-hyperbolic groups . Topology 36(1997), no. 6, 1275–1289. https://doi.org/10.1016/S0040-9383(96)00046-8.Google Scholar
Fujiwara, K., The second bounded cohomology of a group acting on a Gromov-hyperbolic space . Proc. London Math. Soc. (3) 76(1998), no. 1, 70–94. https://doi.org/10.1112/S0024611598000033.Google Scholar
Fujiwara, K., The second bounded cohomology of an amalgamated free product of groups . Trans. Amer. Math. Soc. 352(2000), no. 3, 1113–1129. https://doi.org/10.1090/S0002-9947-99-02282-5.Google Scholar
Fujiwara, K., Quasi-homomorphisms on mapping class groups. In: Handbook of Teichmüller theory. Vol. II, IRMA Lect. Math. Theor. Phys., 13, Eur. Math. Soc., Zürich, 2009, pp. 241–269.Google Scholar
Ghys, E. and de la Harpe, P., Infinite groups as geometric objects (after Gromov). In: Ergodic theory, symbolic dynamics and hyperbolic spaces (Trieste, 1989) Oxford University Press, 1991, pp. 299–314.Google Scholar
Gromov, M., Volume and bounded cohomology . Inst. Hautes Études Sci. Publ. Math. (1982), no. 56, 5–99.Google Scholar
Gromov, M., Hyperbolic groups. In: Essays in group theory, Math. Sci. Res. Inst. Publ., 8, Springer, New York, 1987. https://doi.org/10.1007/978-1-4613-9586-7_3.Google Scholar
Gruber, D. and Sisto, A., Infinitely presented graphical small cancellation groups are acylindrically hyperbolic. Ann. Inst. Fourier., to appear. arxiv:1408.4488.Google Scholar
Hull, M. and Osin, D., Induced quasicocycles on groups with hyperbolically embedded subgroups . Algebr. Geom. Topol. 13(2013), no. 5, 2635–2665. https://doi.org/10.2140/agt.2013.13.2635.Google Scholar
Lyndon, R. and Schupp, P., Combinatorial group theory . Springer-Verlag, Berlin-New York, 1977.Google Scholar
Rips, E. and Sela, Z., Canonical representatives and equations in hyperbolic groups . Invent. Math. 120(1995), no. 3, 489–512. https://doi.org/10.1007/BF01241140.Google Scholar
Sela, Z., Uniform embeddings of hyperbolic groups in Hilbert spaces . Israel J. Math. 80(1992), no. 1–2, 171–181. https://doi.org/10.1007/BF02808160.Google Scholar