Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-31T06:13:11.057Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Actions and Singular Martingales II, The Recognition Problem

Published online by Cambridge University Press:  20 November 2018

Joseph Rosenblatt  and
Michael Taylor
Joseph Rosenblatt
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, Illinois 61801, USA e-mail: jrsnbltt@math.uiuc.edu
Michael Taylor
Affiliation:
Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, USA e-mail: met@math.unc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We continue our investigation in [RST] of a martingale formed by picking a measurable set 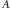$A$ in a compact group 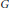$G$ , taking random rotates of 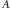$A$ , and considering measures of the resulting intersections, suitably normalized. Here we concentrate on the inverse problem of recognizing 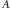$A$ from a small amount of data from this martingale. This leads to problems in harmonic analysis on 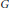$G$ , including an analysis of integrals of products of Gegenbauer polynomials.

Keywords

43A7760B1560G4242C10

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 2 , 01 April 2004 , pp. 431 - 448
Copyright
Copyright © Canadian Mathematical Society 2004

References

[C] Chevalley, C., Theory of Lie Groups. Princeton Univ. Press, Princeton, New Jersey, 1946.Google Scholar
[K] Kahane, J.-P., Some random series of functions. 2nd ed., Cambridge University Press, Cambridge, 1985.Google Scholar
[R1] Rosenblatt, J., Convergence of series of translations. Math. Ann. 230(1977), 245–272.Google Scholar
[R2] Rosenblatt, J., Almost everywhere convergence of series. Math. Ann. 280(1988), 565–577.Google Scholar
[RST] Rosenblatt, J., Stroock, D., and Taylor, M., Group actions and singular martingales. Ergodic Theory Dynamical Systems, to appear.Google Scholar
[Sz] Szegö, G., Orthogonal Polynomials. Amer. Math. Soc., Providence, R.I., 1959.Google Scholar
[T] Taylor, M., Noncommutative Harmonic Analysis. Math. Surveys Monogr., Amer. Math. Soc., Providence, RI, 1986.Google Scholar
[Vil] Vilenkin, N., Special Functions and the Theory of Group Representations. Transl. Math. Monogr. 22, Amer. Math. Soc., Providence, RI, 1968.Google Scholar