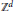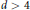Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Lung-Chi
and
Shieh, Narn-Rueih
2006.
CRITICAL BEHAVIOR FOR AN ORIENTED PERCOLATION WITH LONG-RANGE INTERACTIONS IN DIMENSION $d \gt 2$.
Taiwanese Journal of Mathematics,
Vol. 10,
Issue. 5,
Holmes, Mark
2008.
Convergence of Lattice Trees to Super-Brownian Motion above the Critical Dimension.
Electronic Journal of Probability,
Vol. 13,
Issue. none,
Clisby, Nathan
and
Slade, Gordon
2009.
Polygons, Polyominoes and Polycubes.
Vol. 775,
Issue. ,
p.
117.
Slade, Gordon
and
Tomberg, Alexandre
2016.
Critical Correlation Functions for the 4-Dimensional Weakly Self-Avoiding Walk and n-Component $${|\varphi|^4}$$ | φ | 4 Model.
Communications in Mathematical Physics,
Vol. 342,
Issue. 2,
p.
675.