Article contents
Holomorphic Variations of Minimal Disks with Boundary on a Lagrangian Surface
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $L$ be an oriented Lagrangian submanifold in an
$L$ be an oriented Lagrangian submanifold in an  $n$ -dimensional Kähler manifold
$n$ -dimensional Kähler manifold 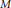 $M$ . Let
$M$ . Let 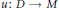 $u:\,D\,\to \,M$ be a minimal immersion from a disk
$u:\,D\,\to \,M$ be a minimal immersion from a disk 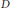 $D$ with
$D$ with 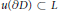 $u(\partial D)\,\subset \,L$ such that
$u(\partial D)\,\subset \,L$ such that 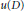 $u(D)$ meets
$u(D)$ meets  $L$ orthogonally along
$L$ orthogonally along 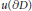 $u(\partial D)$ . Then the real dimension of the space of admissible holomorphic variations is at least
$u(\partial D)$ . Then the real dimension of the space of admissible holomorphic variations is at least 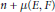 $n\,+\,\mu (E,\,F)$ , where
$n\,+\,\mu (E,\,F)$ , where 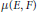 $\mu (E,\,F)$ is a boundary Maslov index; the minimal disk is holomorphic if there exist
$\mu (E,\,F)$ is a boundary Maslov index; the minimal disk is holomorphic if there exist  $n$ admissible holomorphic variations that are linearly independent over
$n$ admissible holomorphic variations that are linearly independent over 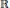 $\mathbb{R}$ at some point
$\mathbb{R}$ at some point 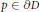 $p\,\in \,\partial D;$ ; if
$p\,\in \,\partial D;$ ; if 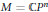 $M=\mathbb{C}{{P}^{n}}$ and
$M=\mathbb{C}{{P}^{n}}$ and  $u$ intersects
$u$ intersects  $L$ positively, then
$L$ positively, then  $u$ is holomorphic if it is stable, and its Morse index is at least
$u$ is holomorphic if it is stable, and its Morse index is at least 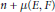 $n\,+\,\mu (E,\,F)$ if
$n\,+\,\mu (E,\,F)$ if  $u$ is unstable.
$u$ is unstable.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
Footnotes
This work is partially supported by NSERC.
References
- 1
- Cited by

