Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-16T22:52:57.859Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy Classification of Projections in the Corona Algebra of a Non-simple C*-algebra

Published online by Cambridge University Press:  20 November 2018

Lawrence G. Brown  and
Hyun Ho Lee
Lawrence G. Brown
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, USA 47907 email: lgb@math.purdue.edu
Hyun Ho Lee
Affiliation:
Department of Mathematics, University of Ulsan, Ulsan, Korea 680-749 email: hadamard@ulsan.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study projections in the corona algebra of 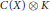$C\left( X \right)\,\otimes \,K$, where $K$ is the 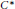${{C}^{*}}$-algebra of compact operators on a separable infinite dimensional Hilbert space and 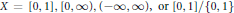$X\,=\,[0,\,1],\,[0,\,\infty ),\,(-\infty ,\,\infty ),\,\text{or}\,\text{ }\!\![\!\!\text{ 0,}\,\text{1 }\!\!]\!\!\text{ / }\!\!\{\!\!\text{ 0,}\,\text{1 }\!\!\}\!\!\text{ }$. Using BDF's essential codimension, we determine conditions for a projection in the corona algebra to be liftable to a projection in the multiplier algebra. We also determine the conditions for two projections to be equal in 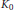${{K}_{0}}$, Murray-von Neumann equivalent, unitarily equivalent, or homotopic. In light of these characterizations, we construct examples showing that the equivalence notions above are all distinct.

Keywords

46L0546L80essential codimensioncontinuous field of Hilbert spacesCorona algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 755 - 777
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Brown, L. G., Ext of certain free product C*-algebras. J. Operator Theory 6(1981), no. 1, 135–141.Google Scholar
[2] Brown, L. G. and Pedersen, G. K., Non-stable K-theory and extremally rich C*-algebras. arxiv:0708.3078V1.Google Scholar
[3] Brown, L. G., Douglas, R. G., and Fillmore, P. A., Unitary equivalence modulo the compact operators and Extensions of C*-algebras. In: Proceedings of a Conference on Operator Theory (Dalhousie Univ., Halifax, N. S., 1973), Lecture Notes in Mathematics, 345, Springer, 1973, pp. 58–128.Google Scholar
[4] Calkin, J. W., Two sided ideals and congruences in the ring of bounded operators in Hilbert space. Ann. of Math 42(1941), 839–873. http://dx.doi.org/10.2307/1968771 Google Scholar
[5] Dadarlat, M. and Eilers, S., Asymptotic unitary equivalence in KK-theory. K-Theory 23(2001), no. 4, 305–322.Google Scholar
[6] Dixmier, J., Position relative de deux variétés linéaires fermées dans un espace de Hilbert. Revue Sci. 86(1948), 387–399.Google Scholar
[7] Dixmier, J., C*-algebras North Holland Mathematical Library, 15, North-Holland, Amsterdam-New York-Oxford, 1977.Google Scholar
[8] Dixmier, J. and Douady, A., Champs continus d’espaces hilbertiens et de C*-algebres. Bull. Soc. Math. France 91(1963), 227–284.Google Scholar
[9] Jacelon, B., A simple, self-absorbing, stably projectionless C*-algebra. arxiv:1006.5397.Google Scholar
[10] Jiang, X. and Su, H., On a simple unital projectionless C*-algebra. Amer. J. Math. 121(1999), no. 2, 359–413. http://dx.doi.org/10.1353/ajm.1999.0012 Google Scholar
[11] Krěin, M. G. and Kranoselśkii, M. A., and Milman, D. P., Defect numbers of linear operators in Banach space and some geometrical problems. (Russian) Sobor. Trudov. Insst. Mat. Akad. Nauk SSSR, 11(1948), 97–112.Google Scholar
[12] Lee, H., Some examples of non-stable K-theory of C*-algebras. Ph. D. dissertation, Purdue University, 2009.Google Scholar
[13] Nagy, G., Some remarks on lifting invertible elements from quotient C*-algebras. J. Operator Theory 21(1989), no. 2, 379–386.Google Scholar
[14] Razak, S., On the classification of simple stably projectionless C*-algebras. Canad. J. Math. 54(2002), no. 1, 138–224. http://dx.doi.org/10.4153/CJM-2002-006-7 Google Scholar
[15] Robert, L. and Tikuisis, A., C*-modules over a commutative C*-algebra. Proc. London Math. Soc. (3) 102(2011), no. 2, 229–256. http://dx.doi.org/10.1112/plms/pdq017 Google Scholar
[16] Rørdam, M. and Winter, W., The Jiang-Su algebra revisited. J. Reine. Angew. Math. 642(2010), 129–155.Google Scholar