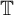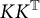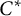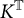1 Introduction
Crossed products have provided some of the most relevant examples in the theory of
![]() $C^*$
-algebras, and the study of their structure and classification is a very active field of research. Moreover, the classification of group actions has a long history within the theory of operator algebras. For example, Connes’ classification of automorphisms of the hyperfinite II
$C^*$
-algebras, and the study of their structure and classification is a very active field of research. Moreover, the classification of group actions has a long history within the theory of operator algebras. For example, Connes’ classification of automorphisms of the hyperfinite II
![]() $_1$
-factor
$_1$
-factor
![]() $\mathcal {R}$
was instrumental in his award-winning classification of amenable factors [Reference Connes4]. Connes’ success motivated significant efforts towards classifying amenable group actions on hyperfinite factors, which culminated almost two decades later.
$\mathcal {R}$
was instrumental in his award-winning classification of amenable factors [Reference Connes4]. Connes’ success motivated significant efforts towards classifying amenable group actions on hyperfinite factors, which culminated almost two decades later.
By comparison to the von Neumann algebra setting, the classification of C*-dynamical systems is a far less developed field of research. A major difficulty is the complicated behavior that finite order automorphisms exhibit at the level of K-theory. Even in the absence of torsion in the acting group, the induced action on the trace space may be wild. These difficulties resulted in a somewhat scattered collection of results, and a lack of a systematic approach. A notable exception is the fruitful analysis of the Rokhlin property in
![]() $C^*$
-algebras, as is seen in the works of Kishimoto [Reference Kishimoto22, Reference Kishimoto23], Matui [Reference Matui26], Nakamura [Reference Nakamura30], Izumi [Reference Izumi16, Reference Izumi17], Sato [Reference Sato39], Nawata [Reference Nawata31], and Gardella [Reference Gardella8] and Gardella and Santiago [Reference Gardella and Santiago13, Reference Gardella and Santiago14], to mention a few.
$C^*$
-algebras, as is seen in the works of Kishimoto [Reference Kishimoto22, Reference Kishimoto23], Matui [Reference Matui26], Nakamura [Reference Nakamura30], Izumi [Reference Izumi16, Reference Izumi17], Sato [Reference Sato39], Nawata [Reference Nawata31], and Gardella [Reference Gardella8] and Gardella and Santiago [Reference Gardella and Santiago13, Reference Gardella and Santiago14], to mention a few.
The advances in Elliott’s classification program (which is by now essentially complete; see [Reference Elliott, Gong, Lin and Niu5, Reference Tikuisis, White and Winter43]) suggest that group actions on purely infinite
![]() $C^*$
-algebras may be more accessible, and there already exist very encouraging results in this direction. In [Reference Szabo42], Szabo proved versions of Kirchberg’s absorption results
$C^*$
-algebras may be more accessible, and there already exist very encouraging results in this direction. In [Reference Szabo42], Szabo proved versions of Kirchberg’s absorption results
![]() ${\mathcal {O}_2}\otimes A\cong {\mathcal {O}_2}$
and
${\mathcal {O}_2}\otimes A\cong {\mathcal {O}_2}$
and
![]() ${\mathcal {O}_{\infty }}\otimes A\cong A$
(with suitable A) for outer actions of amenable groups, using actions on
${\mathcal {O}_{\infty }}\otimes A\cong A$
(with suitable A) for outer actions of amenable groups, using actions on
![]() ${\mathcal {O}_2}$
and
${\mathcal {O}_2}$
and
![]() ${\mathcal {O}_{\infty }}$
which have an appropriate version of the Rokhlin property. (An equivariant version of the absorption result
${\mathcal {O}_{\infty }}$
which have an appropriate version of the Rokhlin property. (An equivariant version of the absorption result
![]() ${\mathcal {O}_2}\otimes A\cong {\mathcal {O}_2}$
was proved for exact groups by Suzuki [Reference Suzuki41].) More recently, Meyer [Reference Meyer27] began exploring the classification of actions of torsion-free amenable groups using
${\mathcal {O}_2}\otimes A\cong {\mathcal {O}_2}$
was proved for exact groups by Suzuki [Reference Suzuki41].) More recently, Meyer [Reference Meyer27] began exploring the classification of actions of torsion-free amenable groups using
![]() $KK^G$
-theory, particularly in what refers to lifting an isomorphism between K-theoretical data to a
$KK^G$
-theory, particularly in what refers to lifting an isomorphism between K-theoretical data to a
![]() $KK^G$
-equivalence. A recurrent issue in this setting is that satisfactory results can only be expected if either the action has some variation of the Rokhlin property, or the group is torsion-free.
$KK^G$
-equivalence. A recurrent issue in this setting is that satisfactory results can only be expected if either the action has some variation of the Rokhlin property, or the group is torsion-free.
In this work, we use equivariant
![]() $KK$
-theory to study circle actions with the Rokhlin property, and obtain
$KK$
-theory to study circle actions with the Rokhlin property, and obtain
![]() ${\mathbb {T}}$
-equivariant versions of celebrated results of Kirchberg concerning simple, purely infinite, separable, nuclear
${\mathbb {T}}$
-equivariant versions of celebrated results of Kirchberg concerning simple, purely infinite, separable, nuclear
![]() $C^*$
-algebras (also known as Kirchberg algebras); see Theorems C and F. By comparison to the continuous Rokhlin property (studied in [Reference Arano and Kubota1] and [Reference Gardella11]), Rokhlin actions are a much richer class with less rigid behavior. Accordingly, more involved arguments are needed in this setting.
$C^*$
-algebras (also known as Kirchberg algebras); see Theorems C and F. By comparison to the continuous Rokhlin property (studied in [Reference Arano and Kubota1] and [Reference Gardella11]), Rokhlin actions are a much richer class with less rigid behavior. Accordingly, more involved arguments are needed in this setting.
The main reason to focus on circle actions is that the combination of one-dimensionality with the fact that
![]() ${\mathbb {T}}$
is a Lie group produces phenomena that cannot be expected beyond this setting. An example of this, which is crucial to our work and already fails for
${\mathbb {T}}$
is a Lie group produces phenomena that cannot be expected beyond this setting. An example of this, which is crucial to our work and already fails for
![]() ${\mathbb {T}}^2$
, is the existence of a predual automorphism:
${\mathbb {T}}^2$
, is the existence of a predual automorphism:
Theorem A (See Theorem 2.3)
Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there exists
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there exists
![]() $\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
such that
$\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
such that
![]() $\alpha $
is conjugate to the dual action
$\alpha $
is conjugate to the dual action
![]() $\widehat {\check {\alpha }}$
.
$\widehat {\check {\alpha }}$
.
We completely characterize the automorphisms that arise as preduals of circle actions with the Rokhlin property (see Proposition 2.8). Using this, we show that every circle action with the Rokhlin property has a naturally associated PExt-class.
Theorem B (See Theorem 3.3)
Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be a Rokhlin action. Then the natural map
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be a Rokhlin action. Then the natural map
![]() $K_0(A^\alpha )\hookrightarrow K_0(A)$
is an injective order-embedding, and there is a canonical pure extension
$K_0(A^\alpha )\hookrightarrow K_0(A)$
is an injective order-embedding, and there is a canonical pure extension
![]() ${\mathrm {Ext}}_\ast (\alpha )$
given by
${\mathrm {Ext}}_\ast (\alpha )$
given by
The fact that the above extension is pure is far from obvious, and it ultimately depends on the existence of a sequence of ucp maps
![]() $A\to A^\alpha $
which are asymptotically multiplicative and asymptotically the identity on
$A\to A^\alpha $
which are asymptotically multiplicative and asymptotically the identity on
![]() $A^\alpha $
.
$A^\alpha $
.
Our most interesting results are related to equivariant
![]() $KK^{\mathbb {T}}$
-theory in the setting of Kirchberg algebras. When A is a Kirchberg algebra, we show that so is
$KK^{\mathbb {T}}$
-theory in the setting of Kirchberg algebras. When A is a Kirchberg algebra, we show that so is
![]() $A^\alpha $
and that
$A^\alpha $
and that
![]() $\check {\alpha }$
is aperiodic (Proposition 4.2), which gives us access to Nakamura’s work [Reference Nakamura30]. We use this to obtain a
$\check {\alpha }$
is aperiodic (Proposition 4.2), which gives us access to Nakamura’s work [Reference Nakamura30]. We use this to obtain a
![]() ${\mathbb {T}}$
-equivariant version of the Kirchberg–Phillips classification theorem for actions with the Rokhlin property:
${\mathbb {T}}$
-equivariant version of the Kirchberg–Phillips classification theorem for actions with the Rokhlin property:
Theorem C (See Theorem 4.6)
Let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
![]() $\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
be actions on unital Kirchberg algebras with the Rokhlin property. Then
$\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
be actions on unital Kirchberg algebras with the Rokhlin property. Then
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are conjugate if and only if they are unitally
$\beta $
are conjugate if and only if they are unitally
![]() $KK^{\mathbb {T}}$
-equivalent. In the presence of the UCT, this is in turn equivalent to the existence of a graded isomorphism
$KK^{\mathbb {T}}$
-equivalent. In the presence of the UCT, this is in turn equivalent to the existence of a graded isomorphism
![]() ${\mathrm {Ext}}_\ast (\alpha )\cong {\mathrm {Ext}}_\ast (\beta )$
, which preserves unit classes and is compatible with suspension shifts (see Definition 4.5).
${\mathrm {Ext}}_\ast (\alpha )\cong {\mathrm {Ext}}_\ast (\beta )$
, which preserves unit classes and is compatible with suspension shifts (see Definition 4.5).
We also obtain a range result in the context of above theorem, showing that the only K-theoretic obstructions are the ones obtained in Theorem B.
Theorem D (See Theorem 4.8)
Let
![]() $K_0$
and
$K_0$
and
![]() $K_1$
be abelian groups, let
$K_1$
be abelian groups, let
![]() $k_0\in K_0$
, and let
$k_0\in K_0$
, and let
![]() $\mathcal {E}_0\in {\mathrm {Ext}}(K_0,K_1)$
and
$\mathcal {E}_0\in {\mathrm {Ext}}(K_0,K_1)$
and
![]() $\mathcal {E}_1\in {\mathrm {Ext}}(K_1,K_0)$
be extensions. The following are equivalent:
$\mathcal {E}_1\in {\mathrm {Ext}}(K_1,K_0)$
be extensions. The following are equivalent:
-
(a) There is a Rokhlin action
 $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital UCT Kirchberg algebra A with
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital UCT Kirchberg algebra A with
 $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong (\mathcal {E}_0,\mathcal {E}_1,k_0)$
.
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong (\mathcal {E}_0,\mathcal {E}_1,k_0)$
. -
(b)
 $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
 $\mathcal {E}_1$
are pure.
$\mathcal {E}_1$
are pure.
Unlike in Kirchberg–Phillips’ classification, in the presence of the UCT it does not suffice to assume that both actions have isomorphic
![]() $K^{\mathbb {T}}$
-theory (this is a big difference with the case of the continuous Rokhlin property [Reference Arano and Kubota1, Reference Gardella11]). It also does not suffice for the actions to have isomorphic Meyer’s L-invariant
$K^{\mathbb {T}}$
-theory (this is a big difference with the case of the continuous Rokhlin property [Reference Arano and Kubota1, Reference Gardella11]). It also does not suffice for the actions to have isomorphic Meyer’s L-invariant
![]() $L_\ast ^{\mathbb {T}}(A,\alpha )=K_\ast ^{\mathbb {T}}(A,\alpha )\oplus K_\ast (A)$
[Reference Meyer27]:
$L_\ast ^{\mathbb {T}}(A,\alpha )=K_\ast ^{\mathbb {T}}(A,\alpha )\oplus K_\ast (A)$
[Reference Meyer27]:
Example E (See Example 4.7)
There exist a UCT Kirchberg algebra A and Rokhlin actions
![]() $\alpha ,\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
such that
$\alpha ,\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
such that
![]() $K_\ast ^{\mathbb {T}}(A,\alpha )\cong K_\ast ^{\mathbb {T}}(A,\beta )$
as
$K_\ast ^{\mathbb {T}}(A,\alpha )\cong K_\ast ^{\mathbb {T}}(A,\beta )$
as
![]() $R({\mathbb {T}})$
-modules, although
$R({\mathbb {T}})$
-modules, although
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are not
$\beta $
are not
![]() $KK^{\mathbb {T}}$
-equivalent. One can even construct the actions so that
$KK^{\mathbb {T}}$
-equivalent. One can even construct the actions so that
![]() $A^\alpha \cong A^\beta $
and
$A^\alpha \cong A^\beta $
and
![]() $A\rtimes _\alpha {\mathbb {T}}\cong A\rtimes _\beta {\mathbb {T}}$
, all satisfying the UCT.
$A\rtimes _\alpha {\mathbb {T}}\cong A\rtimes _\beta {\mathbb {T}}$
, all satisfying the UCT.
The above example shows an interesting phenomenon, which we put into perspective. In Example 10.6 in [Reference Rosenberg and Schochet38], Rosenberg and Schochet construct two circle actions on commutative
![]() $C^*$
-algebras with isomorphic
$C^*$
-algebras with isomorphic
![]() $K^{\mathbb {T}}$
-theory, which are not
$K^{\mathbb {T}}$
-theory, which are not
![]() $KK^{\mathbb {T}}$
-equivalent. In their example, the underlying algebras are not even
$KK^{\mathbb {T}}$
-equivalent. In their example, the underlying algebras are not even
![]() $KK$
-equivalent, so the actions cannot be
$KK$
-equivalent, so the actions cannot be
![]() $KK^{\mathbb {T}}$
-equivalent. As communicated to us by Claude Schochet, Example E is the first construction of two circle actions on the same
$KK^{\mathbb {T}}$
-equivalent. As communicated to us by Claude Schochet, Example E is the first construction of two circle actions on the same
![]() $C^*$
-algebra, satisfying the UCT, with isomorphic fixed point algebras and crossed products, which all satisfy the UCT, and isomorphic
$C^*$
-algebra, satisfying the UCT, with isomorphic fixed point algebras and crossed products, which all satisfy the UCT, and isomorphic
![]() $K^{\mathbb {T}}$
-theory, that are not
$K^{\mathbb {T}}$
-theory, that are not
![]() $KK^{\mathbb {T}}$
-equivalent.
$KK^{\mathbb {T}}$
-equivalent.
With a classification of Rokhlin actions on Kirchberg algebras in terms of
![]() $KK^{\mathbb {T}}$
-theory at our disposal, it is natural to ask which Rokhlin actions are
$KK^{\mathbb {T}}$
-theory at our disposal, it is natural to ask which Rokhlin actions are
![]() $KK^{\mathbb {T}}$
-equivalent to a Rokhlin action on a Kirchberg algebra. As it turns out, Rokhlin actions on Kirchberg algebras represent all separable, nuclear
$KK^{\mathbb {T}}$
-equivalent to a Rokhlin action on a Kirchberg algebra. As it turns out, Rokhlin actions on Kirchberg algebras represent all separable, nuclear
![]() $KK^{\mathbb {T}}$
-classes of Rokhlin actions:
$KK^{\mathbb {T}}$
-classes of Rokhlin actions:
Theorem F (See Theorem 4.15)
Let A be a separable, nuclear, unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
have the Rokhlin property. Then there exist a unique unital Kirchberg algebra D and a unique circle action
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
have the Rokhlin property. Then there exist a unique unital Kirchberg algebra D and a unique circle action
![]() $\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
with the Rokhlin property such that
$\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
with the Rokhlin property such that
![]() $(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
unitally.
$(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
unitally.
The theorem above cannot be extended to actions
![]() $\alpha $
that do not necessarily have the Rokhlin property, since there are obstructions to being
$\alpha $
that do not necessarily have the Rokhlin property, since there are obstructions to being
![]() $KK^{\mathbb {T}}$
-equivalent to a Rokhlin action (for example, as in Theorem B). Theorem F should be compared to Theorem 2.1 of [Reference Meyer27], where Meyer shows that every circle action on a separable, nuclear
$KK^{\mathbb {T}}$
-equivalent to a Rokhlin action (for example, as in Theorem B). Theorem F should be compared to Theorem 2.1 of [Reference Meyer27], where Meyer shows that every circle action on a separable, nuclear
![]() $C^*$
-algebra is
$C^*$
-algebra is
![]() $KK^{\mathbb {T}}$
-equivalent to an outer action on a Kirchberg algebra. It is not clear from Meyer’s construction that the resulting action on the Kirchberg algebra has the Rokhlin property if the original one does. We therefore could not adapt his argument to our context, and instead use older ideas of Kirchberg, applied at the level of the predual
$KK^{\mathbb {T}}$
-equivalent to an outer action on a Kirchberg algebra. It is not clear from Meyer’s construction that the resulting action on the Kirchberg algebra has the Rokhlin property if the original one does. We therefore could not adapt his argument to our context, and instead use older ideas of Kirchberg, applied at the level of the predual
![]() $\check {\alpha }$
.
$\check {\alpha }$
.
The results here presented are an expanded version of Chapter IX of my Ph.D. thesis [Reference Gardella9]. Since the first preprint version of this work appeared on the arxiv, Arano and Kubota generalized the first part of Theorem C to compact groups other than
![]() ${\mathbb {T}}$
(see Proposition 4.8 in [Reference Arano and Kubota1]). The methods are quite different, since we take full advantage of the existence of a predual automorphism. Moreover, for circle actions (as opposed to general compact group actions),
${\mathbb {T}}$
(see Proposition 4.8 in [Reference Arano and Kubota1]). The methods are quite different, since we take full advantage of the existence of a predual automorphism. Moreover, for circle actions (as opposed to general compact group actions),
![]() $KK^{\mathbb {T}}$
-equivalence can be detected via a K-theoretical invariant in the presence of the UCT, and the range of this invariant can be completely described. This makes the classification of circle actions with the Rokhlin property comparatively more accessible than that of general compact groups. Even more recently, Gabe and Szabo obtained in [Reference Gabe and Szabo7] an equivariant version of the Kirchberg–Phillips classification for amenable actions that are “isometrically shift-absorbing.” These developments subsumeFootnote
1
the part of Theorem C which does not assume the UCT, using significantly heavier machinery, but do not have overlap with the other results here stated. In this sense, our proof Theorem C should be regarded as a shorter and simpler proof of [Reference Gabe and Szabo7, Theorem F] in the case of Rokhlin actions of the circle.
$KK^{\mathbb {T}}$
-equivalence can be detected via a K-theoretical invariant in the presence of the UCT, and the range of this invariant can be completely described. This makes the classification of circle actions with the Rokhlin property comparatively more accessible than that of general compact groups. Even more recently, Gabe and Szabo obtained in [Reference Gabe and Szabo7] an equivariant version of the Kirchberg–Phillips classification for amenable actions that are “isometrically shift-absorbing.” These developments subsumeFootnote
1
the part of Theorem C which does not assume the UCT, using significantly heavier machinery, but do not have overlap with the other results here stated. In this sense, our proof Theorem C should be regarded as a shorter and simpler proof of [Reference Gabe and Szabo7, Theorem F] in the case of Rokhlin actions of the circle.
2 Duality for circle actions with the Rokhlin property
In this section, we study the Rokhlin property for circle actions in connection to duality. There are two main results in this section. First, it is shown that every circle action with the Rokhlin property is a dual action, that is, there is an automorphism of the fixed point algebra whose dual action is conjugate to the given one (see Theorem 2.3). Such an automorphism is essentially unique, and is called the predual automorphism. Second, we characterize those automorphisms that are predual to a circle action with the Rokhlin property (see Proposition 2.8).
We begin by recalling the definition of the Rokhlin property for a circle action (Definition 3.2 in [Reference Hirshberg and Winter15]) in a way that is useful for our purposes.
Definition 2.1 Let A be a unital
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action. We say that
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action. We say that
![]() $\alpha $
has the Rokhlin property if for every
$\alpha $
has the Rokhlin property if for every
![]() $\varepsilon>0$
and every compact subset
$\varepsilon>0$
and every compact subset
![]() $F\subseteq A$
, there exists a unitary
$F\subseteq A$
, there exists a unitary
![]() $u\in {\mathcal {U}}(A)$
such that:
$u\in {\mathcal {U}}(A)$
such that:
-
(a)
 $\|\alpha _ z(u)- z u\|<\varepsilon $
for all
$\|\alpha _ z(u)- z u\|<\varepsilon $
for all
 $ z\in {\mathbb {T}}$
.
$ z\in {\mathbb {T}}$
. -
(b)
 $\|ua-au\|<\varepsilon $
for all
$\|ua-au\|<\varepsilon $
for all
 $a\in F$
.
$a\in F$
.
Next, we show that we can replace the unitary u in the above definition by a nearby unitary which satisfies condition (a) exactly. In the terminology of [Reference Phillips36], the following shows that the action of
![]() ${\mathbb {T}}$
on
${\mathbb {T}}$
on
![]() $C({\mathbb {T}})$
is equivariantly semiprojective.
$C({\mathbb {T}})$
is equivariantly semiprojective.
Proposition 2.2 For every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta>0$
with the following property: whenever
$\delta>0$
with the following property: whenever
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
is an action on a unital
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
is an action on a unital
![]() $C^*$
-algebra A and
$C^*$
-algebra A and
![]() $u\in {\mathcal {U}}(A)$
is a unitary satisfying
$u\in {\mathcal {U}}(A)$
is a unitary satisfying
![]() $\|\alpha _ z(u)- z u\|<\delta $
for all
$\|\alpha _ z(u)- z u\|<\delta $
for all
![]() $ z\in {\mathbb {T}}$
, then there exists a unitary
$ z\in {\mathbb {T}}$
, then there exists a unitary
![]() $v\in {\mathcal {U}}(A)$
with
$v\in {\mathcal {U}}(A)$
with
![]() $\|u-v\|<\varepsilon $
and
$\|u-v\|<\varepsilon $
and
![]() $\alpha _ z(v)= z v$
for all
$\alpha _ z(v)= z v$
for all
![]() $ z\in {\mathbb {T}}$
.
$ z\in {\mathbb {T}}$
.
Proof Given
![]() $\varepsilon>0$
, choose
$\varepsilon>0$
, choose
![]() $\delta <\frac {1}{3}$
small enough so that
$\delta <\frac {1}{3}$
small enough so that
Let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
![]() $u\in {\mathcal {U}}(A)$
be as in the statement. Set
$u\in {\mathcal {U}}(A)$
be as in the statement. Set
![]() $x =\int _{{\mathbb {T}}}\overline { z}\alpha _ z(u)\ d z\in A$
. Then
$x =\int _{{\mathbb {T}}}\overline { z}\alpha _ z(u)\ d z\in A$
. Then
![]() $\|x\|\leq 1$
and
$\|x\|\leq 1$
and
![]() $\|x-u\|\leq \delta $
. One checks that
$\|x-u\|\leq \delta $
. One checks that
![]() $\|x^*x-1\|\leq 2\delta < 1$
, so
$\|x^*x-1\|\leq 2\delta < 1$
, so
![]() $x^*x$
is invertible. Moreover,
$x^*x$
is invertible. Moreover,
Set
![]() $u= x(x^*x)^{-\frac {1}{2}}$
. Then u is a unitary in A. Using that
$u= x(x^*x)^{-\frac {1}{2}}$
. Then u is a unitary in A. Using that
![]() $\|x\|\leq 1$
at the first step, and that
$\|x\|\leq 1$
at the first step, and that
![]() $0 \leq 1- (x^*x)^{\frac {1}{2}} \leq 1- x^*x$
at the second step, we get
$0 \leq 1- (x^*x)^{\frac {1}{2}} \leq 1- x^*x$
at the second step, we get
 $$ \begin{align*} \|u-x\| &\leq \big\|(x^*x)^{-\frac{1}{2}}-1\big\| \leq \big\|(x^*x)^{-\frac{1}{2}}\big\| \big\|1-(x^*x)^{\frac{1}{2}}\big\|\\ &\stackrel{(2.2)}{\leq} \frac{1}{\sqrt{1-2\delta}} \|1-x^*x\| \leq \frac{2\delta}{\sqrt{1-2\delta}}. \end{align*} $$
$$ \begin{align*} \|u-x\| &\leq \big\|(x^*x)^{-\frac{1}{2}}-1\big\| \leq \big\|(x^*x)^{-\frac{1}{2}}\big\| \big\|1-(x^*x)^{\frac{1}{2}}\big\|\\ &\stackrel{(2.2)}{\leq} \frac{1}{\sqrt{1-2\delta}} \|1-x^*x\| \leq \frac{2\delta}{\sqrt{1-2\delta}}. \end{align*} $$
Thus
For
![]() $ z\in {\mathbb {T}}$
, we have
$ z\in {\mathbb {T}}$
, we have
It follows that
![]() $\alpha _ z(x^*x)=x^*x$
and hence
$\alpha _ z(x^*x)=x^*x$
and hence
![]() $\alpha _ z(u)=\alpha _ z\big (x(x^*x)^{-\frac {1}{2}}\big )= z u$
, for all
$\alpha _ z(u)=\alpha _ z\big (x(x^*x)^{-\frac {1}{2}}\big )= z u$
, for all
![]() $ z\in {\mathbb {T}}$
, so u satisfies the condition in the statement.
$ z\in {\mathbb {T}}$
, so u satisfies the condition in the statement.
It follows from Proposition 2.2 that condition (1) in Definition 2.1 can be replaced with
![]() $\alpha _ z(u)= z u$
for all
$\alpha _ z(u)= z u$
for all
![]() $ z\in {\mathbb {T}}$
.
$ z\in {\mathbb {T}}$
.
Theorem 2.3 Let A be a unital
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property.
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property.
-
(1) There exists an automorphism
 $\theta \in {\mathrm {Aut}}(A^\alpha )$
such that
$\theta \in {\mathrm {Aut}}(A^\alpha )$
such that
 $(A^\alpha \rtimes _\theta {\mathbb {Z}},\widehat {\theta })$
is conjugate to
$(A^\alpha \rtimes _\theta {\mathbb {Z}},\widehat {\theta })$
is conjugate to
 $(A,\alpha )$
.
$(A,\alpha )$
. -
(2) If
 $\theta '\in {\mathrm {Aut}}(A^\alpha )$
is another automorphism for which
$\theta '\in {\mathrm {Aut}}(A^\alpha )$
is another automorphism for which
 $(A^\alpha \rtimes _{\theta '}{\mathbb {Z}},\widehat {\theta '})$
is conjugate to
$(A^\alpha \rtimes _{\theta '}{\mathbb {Z}},\widehat {\theta '})$
is conjugate to
 $(A,\alpha )$
, then there is a unitary
$(A,\alpha )$
, then there is a unitary
 $w\in A^\alpha $
such that
$w\in A^\alpha $
such that
 $\theta ={\mathrm {Ad}}(w)\circ \theta '$
.
$\theta ={\mathrm {Ad}}(w)\circ \theta '$
.
Proof (1). Using Proposition 2.2, let
![]() $u\in {\mathcal {U}}(A)$
be a unitary satisfying
$u\in {\mathcal {U}}(A)$
be a unitary satisfying
![]() $\alpha _z (u)= z u$
for all
$\alpha _z (u)= z u$
for all
![]() $ z \in {\mathbb {T}}$
. For
$ z \in {\mathbb {T}}$
. For
![]() $a\in A^\alpha $
, we have
$a\in A^\alpha $
, we have
![]() $\alpha _z (uau^*)=uau^*$
for all
$\alpha _z (uau^*)=uau^*$
for all
![]() $ z \in {\mathbb {T}}$
, and thus conjugation by u determines an automorphism
$ z \in {\mathbb {T}}$
, and thus conjugation by u determines an automorphism
![]() $\theta $
of
$\theta $
of
![]() $A^\alpha $
. Let
$A^\alpha $
. Let
![]() $v\in A^\alpha \rtimes _\theta {\mathbb {Z}}$
denote the canonical unitary implementing
$v\in A^\alpha \rtimes _\theta {\mathbb {Z}}$
denote the canonical unitary implementing
![]() $\theta $
. Since the pair
$\theta $
. Since the pair
![]() $({\mathrm {id}}_{A^\alpha }, u)$
is a covariant representation of
$({\mathrm {id}}_{A^\alpha }, u)$
is a covariant representation of
![]() $(A^\alpha ,\theta )$
on A, there is a unique homomorphism
$(A^\alpha ,\theta )$
on A, there is a unique homomorphism
![]() $\varphi \colon A^\alpha \rtimes _\theta {\mathbb {Z}}\to A$
satisfying
$\varphi \colon A^\alpha \rtimes _\theta {\mathbb {Z}}\to A$
satisfying
![]() $\varphi (a)=a$
for all
$\varphi (a)=a$
for all
![]() $a\in A^\alpha $
and
$a\in A^\alpha $
and
![]() $\varphi (v)=u$
.
$\varphi (v)=u$
.
We claim that
![]() $\varphi $
is an equivariant isomorphism. Equivariance of
$\varphi $
is an equivariant isomorphism. Equivariance of
![]() $\varphi $
is clear, since for all
$\varphi $
is clear, since for all
![]() $ z \in {\mathbb {T}}$
we have
$ z \in {\mathbb {T}}$
we have
![]() $\widehat {\theta }_z (a)=a$
for all
$\widehat {\theta }_z (a)=a$
for all
![]() $a\in A^\alpha $
and
$a\in A^\alpha $
and
![]() $\widehat {\theta }_z (v)= z v$
. Injectivity of
$\widehat {\theta }_z (v)= z v$
. Injectivity of
![]() $\varphi $
follows from the fact that
$\varphi $
follows from the fact that
![]() ${\mathrm {id}}_{A^\alpha }$
is injective (and that
${\mathrm {id}}_{A^\alpha }$
is injective (and that
![]() ${\mathbb {Z}}$
is amenable). Surjectivity can be deduced using spectral subspaces, as follows. Given
${\mathbb {Z}}$
is amenable). Surjectivity can be deduced using spectral subspaces, as follows. Given
![]() $n\in {\mathbb {Z}}$
, we set
$n\in {\mathbb {Z}}$
, we set
which is a closed subspace of A. It is well-known that
![]() $\sum _{n\in {\mathbb {Z}}}A_n$
is dense in A; see, for example, part (ix) of Theorem 8.1.4 in [Reference Pedersen34]. Note that
$\sum _{n\in {\mathbb {Z}}}A_n$
is dense in A; see, for example, part (ix) of Theorem 8.1.4 in [Reference Pedersen34]. Note that
![]() $A_0=A^\alpha $
and that u belongs to
$A_0=A^\alpha $
and that u belongs to
![]() $A_1$
. Moreover, using that u is a unitary, it is easy to see that
$A_1$
. Moreover, using that u is a unitary, it is easy to see that
![]() $A_n=u^nA_0$
for all
$A_n=u^nA_0$
for all
![]() $n\in {\mathbb {Z}}$
. In particular, A is generated as a
$n\in {\mathbb {Z}}$
. In particular, A is generated as a
![]() $C^*$
-algebra by
$C^*$
-algebra by
![]() $A_0$
and u. Since
$A_0$
and u. Since
![]() $A_0\cup \{u\}$
is contained in the image of
$A_0\cup \{u\}$
is contained in the image of
![]() $\varphi $
, we conclude that
$\varphi $
, we conclude that
![]() $\varphi $
is surjective.
$\varphi $
is surjective.
(2). Let
![]() $\theta '$
be as in the statement, and let
$\theta '$
be as in the statement, and let
![]() $\varphi \colon (A^\alpha \rtimes _{\theta }{\mathbb {Z}},\widehat {\theta })\to (A,\alpha )$
and
$\varphi \colon (A^\alpha \rtimes _{\theta }{\mathbb {Z}},\widehat {\theta })\to (A,\alpha )$
and
![]() $\varphi '\colon (A^\alpha \rtimes _{\theta '}{\mathbb {Z}},\widehat {\theta '})\to (A,\alpha )$
be equivariant isomorphisms. Let v be the canonical unitary in
$\varphi '\colon (A^\alpha \rtimes _{\theta '}{\mathbb {Z}},\widehat {\theta '})\to (A,\alpha )$
be equivariant isomorphisms. Let v be the canonical unitary in
![]() $A^\alpha \rtimes _\theta {\mathbb {Z}}$
that implements
$A^\alpha \rtimes _\theta {\mathbb {Z}}$
that implements
![]() $\theta $
, and let
$\theta $
, and let
![]() $v'$
be the canonical unitary in
$v'$
be the canonical unitary in
![]() $A^\alpha \rtimes _{\theta '}{\mathbb {Z}}$
that implements
$A^\alpha \rtimes _{\theta '}{\mathbb {Z}}$
that implements
![]() $\theta '$
. Set
$\theta '$
. Set
![]() $w=\varphi (v)\varphi '(v')^*$
, which is a unitary in A. We claim that w is fixed by
$w=\varphi (v)\varphi '(v')^*$
, which is a unitary in A. We claim that w is fixed by
![]() $\alpha $
. For
$\alpha $
. For
![]() $ z\in {\mathbb {T}}$
, we use equivariance of
$ z\in {\mathbb {T}}$
, we use equivariance of
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
to get
$\varphi '$
to get
Finally, given
![]() $a\in A^\alpha $
, we have
$a\in A^\alpha $
, we have
 $$ \begin{align*}({\mathrm{Ad}}(w)\circ\theta)(a)&=(\varphi(v)\varphi'(v')^*)(\varphi'(v')a\varphi'(v')^*)(\varphi'(v')\varphi(v)^*)\\ &=\varphi(v)a\varphi(v)^*=\theta'(a).\\[-34pt] \end{align*} $$
$$ \begin{align*}({\mathrm{Ad}}(w)\circ\theta)(a)&=(\varphi(v)\varphi'(v')^*)(\varphi'(v')a\varphi'(v')^*)(\varphi'(v')\varphi(v)^*)\\ &=\varphi(v)a\varphi(v)^*=\theta'(a).\\[-34pt] \end{align*} $$
Definition 2.4 Let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. In view of Theorem 2.3, we denote by
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. In view of Theorem 2.3, we denote by
![]() $\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
the unique automorphism for which
$\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
the unique automorphism for which
![]() $\widehat {\check {\alpha }}$
is conjugate to
$\widehat {\check {\alpha }}$
is conjugate to
![]() $\alpha $
. We call
$\alpha $
. We call
![]() $\check {\alpha }$
the predual automorphism of
$\check {\alpha }$
the predual automorphism of
![]() $\alpha $
.
$\alpha $
.
Corollary 2.5 Let A be a
![]() $C^*$
-algebra and let
$C^*$
-algebra and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there is a natural isomorphism
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there is a natural isomorphism
![]() $A\rtimes _\alpha {\mathbb {T}}\cong A^\alpha \otimes {\mathcal {K}}(L^2({\mathbb {T}}))$
.
$A\rtimes _\alpha {\mathbb {T}}\cong A^\alpha \otimes {\mathcal {K}}(L^2({\mathbb {T}}))$
.
Proof This is an immediate from Theorem 2.3 and Takai duality.
Obtaining a characterization of those automorphisms that arise as preduals of Rokhlin actions as in Definition 2.4 will be a critical tool in the rest of this work. Such a characterization is obtained in Proposition 2.8, using the following notion:
Definition 2.6 Let B be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\beta $
be an automorphism of B. Then
$\beta $
be an automorphism of B. Then
![]() $\beta $
is said to be approximately representable if for every finite subset
$\beta $
is said to be approximately representable if for every finite subset
![]() $F\subseteq B$
and every
$F\subseteq B$
and every
![]() $\varepsilon>0$
, there exists a contraction
$\varepsilon>0$
, there exists a contraction
![]() $v\in B$
satisfying:
$v\in B$
satisfying:
-
(a)
 $\|v^*v-vv^*\|<\varepsilon $
;
$\|v^*v-vv^*\|<\varepsilon $
; -
(b)
 $\|v^*vb-b\|<\varepsilon $
for all
$\|v^*vb-b\|<\varepsilon $
for all
 $b\in F$
;
$b\in F$
; -
(c)
 $\|\beta (v)-v\|<\varepsilon $
; and
$\|\beta (v)-v\|<\varepsilon $
; and -
(d)
 $\|\beta (b)-vbv^*\|<\varepsilon $
for all
$\|\beta (b)-vbv^*\|<\varepsilon $
for all
 $b\in F$
.
$b\in F$
.
Using functional calculus, it is clear that the contraction v in the above definition can be chosen to be a unitary whenever B is unital. In particular, approximately representable automorphisms of unital
![]() $C^*$
-algebras are approximately inner.
$C^*$
-algebras are approximately inner.
Remark 2.7 We endow
![]() ${\mathbb {T}}$
with its Haar probability measure. For an action
${\mathbb {T}}$
with its Haar probability measure. For an action
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital
![]() $C^*$
-algebra A, we endow
$C^*$
-algebra A, we endow
![]() $L^1({\mathbb {T}},A)$
with the usual
$L^1({\mathbb {T}},A)$
with the usual
![]() $L^1$
-norm
$L^1$
-norm
![]() $\|\cdot \|_1$
and the operations of twisted convolution and involution
$\|\cdot \|_1$
and the operations of twisted convolution and involution
for all
![]() $\xi ,\eta \in L^1({\mathbb {T}},A)$
and all
$\xi ,\eta \in L^1({\mathbb {T}},A)$
and all
![]() $z\in {\mathbb {T}}$
. Then
$z\in {\mathbb {T}}$
. Then
![]() $L^1({\mathbb {T}},A)$
is a dense
$L^1({\mathbb {T}},A)$
is a dense
![]() $\ast $
-subalgebra of
$\ast $
-subalgebra of
![]() $A\rtimes _\alpha {\mathbb {T}}$
, and the canonical inclusion is contractive with respect to the
$A\rtimes _\alpha {\mathbb {T}}$
, and the canonical inclusion is contractive with respect to the
![]() $L^1$
-norm on
$L^1$
-norm on
![]() $L^1({\mathbb {T}},A)$
and the
$L^1({\mathbb {T}},A)$
and the
![]() $C^*$
-norm on
$C^*$
-norm on
![]() $A\rtimes _\alpha {\mathbb {T}}$
. Recall that there is a canonical nondegenerate inclusion
$A\rtimes _\alpha {\mathbb {T}}$
. Recall that there is a canonical nondegenerate inclusion
![]() $C^*({\mathbb {T}})\subseteq A\rtimes _\alpha {\mathbb {T}}$
; in particular, any (contractive) approximate identity for
$C^*({\mathbb {T}})\subseteq A\rtimes _\alpha {\mathbb {T}}$
; in particular, any (contractive) approximate identity for
![]() $C^*({\mathbb {T}})$
is also a (contractive) approximate identity for
$C^*({\mathbb {T}})$
is also a (contractive) approximate identity for
![]() $A\rtimes _\alpha {\mathbb {T}}$
. Recall that the dual automorphism
$A\rtimes _\alpha {\mathbb {T}}$
. Recall that the dual automorphism
![]() $\widehat {\alpha }\in {\mathrm {Aut}}(A\rtimes _\alpha {\mathbb {T}})$
is given by
$\widehat {\alpha }\in {\mathrm {Aut}}(A\rtimes _\alpha {\mathbb {T}})$
is given by
![]() $\widehat {\alpha }(fa)(z)=z f(z)a$
for all
$\widehat {\alpha }(fa)(z)=z f(z)a$
for all
![]() $z\in {\mathbb {T}}$
.
$z\in {\mathbb {T}}$
.
Next, we show that approximate representability is dual to the Rokhlin property.
Proposition 2.8 Let A be a unital
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action, and let
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action, and let
![]() $\beta \in {\mathrm {Aut}}(A)$
be an automorphism.
$\beta \in {\mathrm {Aut}}(A)$
be an automorphism.
-
(1) The action
 $\alpha $
has the Rokhlin property if and only if
$\alpha $
has the Rokhlin property if and only if
 $\widehat {\alpha }\in {\mathrm {Aut}}(A\rtimes _\alpha {\mathbb {T}})$
is approximately representable.
$\widehat {\alpha }\in {\mathrm {Aut}}(A\rtimes _\alpha {\mathbb {T}})$
is approximately representable. -
(2) The automorphism
 $\beta $
is approximately representable if and only if
$\beta $
is approximately representable if and only if
 $\widehat {\beta }\colon {\mathbb {T}}\to {\mathrm {Aut}}(A\rtimes _\beta {\mathbb {Z}})$
has the Rokhlin property.
$\widehat {\beta }\colon {\mathbb {T}}\to {\mathrm {Aut}}(A\rtimes _\beta {\mathbb {Z}})$
has the Rokhlin property.
Proof (1). Assume that
![]() $\alpha $
has the Rokhlin property. Let
$\alpha $
has the Rokhlin property. Let
![]() $F\subseteq A\rtimes _\alpha {\mathbb {T}}$
be a finite subset, and let
$F\subseteq A\rtimes _\alpha {\mathbb {T}}$
be a finite subset, and let
![]() $\varepsilon>0$
. For
$\varepsilon>0$
. For
![]() $\xi \in L^1({\mathbb {T}})$
and
$\xi \in L^1({\mathbb {T}})$
and
![]() $a\in A$
, write
$a\in A$
, write
![]() $\xi a$
for the for the function given by
$\xi a$
for the for the function given by
![]() $(\xi a)(z)=\xi (z)a$
for all
$(\xi a)(z)=\xi (z)a$
for all
![]() $z\in {\mathbb {T}}$
. Since the linear span of the elements of this form is dense in
$z\in {\mathbb {T}}$
. Since the linear span of the elements of this form is dense in
![]() $L^1({\mathbb {T}},A)$
, and hence, also in
$L^1({\mathbb {T}},A)$
, and hence, also in
![]() $A\rtimes _\alpha {\mathbb {T}}$
, we may assume that there exist finite subsets
$A\rtimes _\alpha {\mathbb {T}}$
, we may assume that there exist finite subsets
![]() $F_A\subseteq A$
and
$F_A\subseteq A$
and
![]() $F_{\mathbb {T}}\subseteq L^1({\mathbb {T}})$
such that every element of F has the form
$F_{\mathbb {T}}\subseteq L^1({\mathbb {T}})$
such that every element of F has the form
![]() $\xi a$
for
$\xi a$
for
![]() $a\in F_A$
and
$a\in F_A$
and
![]() $\xi \in F_{\mathbb {T}}$
. Without loss of generality, we may assume that the sets
$\xi \in F_{\mathbb {T}}$
. Without loss of generality, we may assume that the sets
![]() $F_A$
and
$F_A$
and
![]() $F_{\mathbb {T}}$
contain only self-adjoint contractions.
$F_{\mathbb {T}}$
contain only self-adjoint contractions.
Let
![]() $f\colon {\mathbb {T}}\to {\mathbb {C}}$
be a positive, continuous function whose support is a small enough neighborhood of
$f\colon {\mathbb {T}}\to {\mathbb {C}}$
be a positive, continuous function whose support is a small enough neighborhood of
![]() $1\in {\mathbb {T}}$
so that the following conditions are satisfied:
$1\in {\mathbb {T}}$
so that the following conditions are satisfied:
-
(i)
 $\|(f\ast f)b-b\|<\varepsilon $
for all
$\|(f\ast f)b-b\|<\varepsilon $
for all
 $b\in F\cup \widehat {\alpha }(F)$
;
$b\in F\cup \widehat {\alpha }(F)$
; -
(ii)
 $\|f\|_1=1=\|f\ast f\|_1$
;
$\|f\|_1=1=\|f\ast f\|_1$
; -
(iii)
 $f(z)=f(\overline {z})$
for all
$f(z)=f(\overline {z})$
for all
 $z\in {\mathbb {T}}$
;
$z\in {\mathbb {T}}$
; -
(iv) with
 $\widetilde {f}(z)=z f(z)$
for all
$\widetilde {f}(z)=z f(z)$
for all
 $z\in {\mathbb {T}}$
, we have
$z\in {\mathbb {T}}$
, we have  $$\begin{align*}\|f-\widetilde{f}\|_1<\varepsilon \ \ \mbox{ and } \ \ \|f\ast f-\widetilde{f}\ast \widetilde{f}\|_1<\varepsilon; \end{align*}$$
$$\begin{align*}\|f-\widetilde{f}\|_1<\varepsilon \ \ \mbox{ and } \ \ \|f\ast f-\widetilde{f}\ast \widetilde{f}\|_1<\varepsilon; \end{align*}$$
-
(v) given
 $\xi \in F_{\mathbb {T}}$
and
$\xi \in F_{\mathbb {T}}$
and
 $a\in F_A$
, if
$a\in F_A$
, if
 $z,\sigma ,\omega \in {\mathbb {T}}$
satisfy
$z,\sigma ,\omega \in {\mathbb {T}}$
satisfy
 $f(\omega )f(\overline {z}\sigma \omega )\neq 0$
, then
$f(\omega )f(\overline {z}\sigma \omega )\neq 0$
, then  $$\begin{align*}\|\alpha_\omega(a)-a\|<\frac{\varepsilon}{2} \ \ \mbox{ and } \ \ |\xi(\sigma)-\xi(z)|<\frac{\varepsilon}{2}. \end{align*}$$
$$\begin{align*}\|\alpha_\omega(a)-a\|<\frac{\varepsilon}{2} \ \ \mbox{ and } \ \ |\xi(\sigma)-\xi(z)|<\frac{\varepsilon}{2}. \end{align*}$$
Using Proposition 2.2, find a unitary
![]() $u\in A$
satisfying:
$u\in A$
satisfying:
-
(vi)
 $\alpha _\zeta (u)=\zeta u$
for all
$\alpha _\zeta (u)=\zeta u$
for all
 $\zeta \in {\mathbb {T}}$
, and
$\zeta \in {\mathbb {T}}$
, and -
(vii)
 $\|ua-au\|<\varepsilon /2$
for all
$\|ua-au\|<\varepsilon /2$
for all
 $a\in \bigcup _{\omega \in {\mathbb {T}}}\alpha _\omega (F_A)$
.
$a\in \bigcup _{\omega \in {\mathbb {T}}}\alpha _\omega (F_A)$
.
We regard u as a unitary in the multiplier algebra of
![]() $A\rtimes _\alpha {\mathbb {T}}$
via the canonical unital embedding
$A\rtimes _\alpha {\mathbb {T}}$
via the canonical unital embedding
![]() $A\hookrightarrow M(A\rtimes _\alpha {\mathbb {T}})$
, and set
$A\hookrightarrow M(A\rtimes _\alpha {\mathbb {T}})$
, and set
![]() $v=fu^*$
. Then v is a contraction in
$v=fu^*$
. Then v is a contraction in
![]() $L^1({\mathbb {T}},A)$
, and hence also in
$L^1({\mathbb {T}},A)$
, and hence also in
![]() $A\rtimes _\alpha {\mathbb {T}}$
. We proceed to check the conditions in Definition 2.6. Let
$A\rtimes _\alpha {\mathbb {T}}$
. We proceed to check the conditions in Definition 2.6. Let
![]() $z\in {\mathbb {T}}$
. Then
$z\in {\mathbb {T}}$
. Then
 $$ \begin{align*} (v^*\ast v)(z) &= \int_{\mathbb{T}} v^*(\omega)\alpha_\omega(v(\overline{\omega}z))\ d\omega = \int_{\mathbb{T}} \omega f(\omega)u\alpha_\omega(f(\overline{\omega}z)u^*)\ d\omega\\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}} \omega f(\omega)uf(\overline{\omega}z)\overline{\omega}u^*\ d\omega = (f\ast f)(z). \end{align*} $$
$$ \begin{align*} (v^*\ast v)(z) &= \int_{\mathbb{T}} v^*(\omega)\alpha_\omega(v(\overline{\omega}z))\ d\omega = \int_{\mathbb{T}} \omega f(\omega)u\alpha_\omega(f(\overline{\omega}z)u^*)\ d\omega\\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}} \omega f(\omega)uf(\overline{\omega}z)\overline{\omega}u^*\ d\omega = (f\ast f)(z). \end{align*} $$
Thus,
![]() $v^*\ast v=f\ast f$
and hence condition (a) in Definition 2.6 follows from condition (ii) above. In order to check (b), we compute as follows for
$v^*\ast v=f\ast f$
and hence condition (a) in Definition 2.6 follows from condition (ii) above. In order to check (b), we compute as follows for
![]() $z\in {\mathbb {T}}$
:
$z\in {\mathbb {T}}$
:
 $$ \begin{align*} (v\ast v^*)(z) &= \int_{\mathbb{T}} v(\omega)\alpha_\omega(v^*(\overline{\omega}z))\ d\omega = \int_{\mathbb{T}} f(\omega)u^*\alpha_\omega(\overline{\omega}z f(\overline{\omega}z)u)\ d\omega\\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}} f(\omega)u^*\overline{\omega}z f(\overline{\omega}z)\omega u\ d\omega = \int_{\mathbb{T}} \omega f(\omega)\overline{\omega}z f(\overline{\omega}z)\ d\omega = (\widetilde{f}\ast \widetilde{f})(z). \end{align*} $$
$$ \begin{align*} (v\ast v^*)(z) &= \int_{\mathbb{T}} v(\omega)\alpha_\omega(v^*(\overline{\omega}z))\ d\omega = \int_{\mathbb{T}} f(\omega)u^*\alpha_\omega(\overline{\omega}z f(\overline{\omega}z)u)\ d\omega\\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}} f(\omega)u^*\overline{\omega}z f(\overline{\omega}z)\omega u\ d\omega = \int_{\mathbb{T}} \omega f(\omega)\overline{\omega}z f(\overline{\omega}z)\ d\omega = (\widetilde{f}\ast \widetilde{f})(z). \end{align*} $$
Thus
![]() $v\ast v^*=\widetilde {f}\ast \widetilde {f}$
. We deduce that
$v\ast v^*=\widetilde {f}\ast \widetilde {f}$
. We deduce that
as desired. In order to check (c), let
![]() $\zeta \in {\mathbb {T}}$
. Then
$\zeta \in {\mathbb {T}}$
. Then
so
![]() $\widehat {\alpha }(v)=\widetilde {f}u^*$
. Using this at the second step, we get
$\widehat {\alpha }(v)=\widetilde {f}u^*$
. Using this at the second step, we get
as desired. Finally, in order to check (d), it suffices to take
![]() $\xi \in F_{\mathbb {T}}$
and
$\xi \in F_{\mathbb {T}}$
and
![]() $a\in F_A$
, and show the desired inequality for
$a\in F_A$
, and show the desired inequality for
![]() $b=\xi a$
. Given
$b=\xi a$
. Given
![]() $z\in {\mathbb {T}}$
, we have
$z\in {\mathbb {T}}$
, we have
 $$ \begin{align*} (v\ast b \ast v^*)(z) &=\int_{\mathbb{T}} v(\omega)\alpha_\omega((b \ast v^*)(\overline{\omega}z)) \ d\omega \\ &=\int_{\mathbb{T}} f(\omega)u^*\alpha_\omega\Big( \int_{\mathbb{T}} \xi(\sigma)a \alpha_\sigma(v^*(\overline{\sigma\omega}z)) \ d\sigma \Big) d\omega \\ &=\int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega)u^*\xi(\sigma)\alpha_\omega(a) \alpha_{\omega\sigma }\big(\overline{\sigma\omega}z f(\overline{\sigma\omega}z)u \big) d\sigma d\omega \\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega)u^* \xi(\sigma)\alpha_\omega(a) \overline{\sigma\omega}z f(\overline{\sigma\omega}z) \omega\sigma u \ d\sigma d\omega \\ &= z\int_{\mathbb{T}}\int_{\mathbb{T}} \xi(\sigma)u^*\alpha_\omega(a)u f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega\\ &\stackrel{\mathrm{(vii)}}{\approx}_{\!\!\frac{\varepsilon}{2}} z\int_{\mathbb{T}}\int_{\mathbb{T}} \xi(\sigma)\alpha_\omega(a) f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega. \end{align*} $$
$$ \begin{align*} (v\ast b \ast v^*)(z) &=\int_{\mathbb{T}} v(\omega)\alpha_\omega((b \ast v^*)(\overline{\omega}z)) \ d\omega \\ &=\int_{\mathbb{T}} f(\omega)u^*\alpha_\omega\Big( \int_{\mathbb{T}} \xi(\sigma)a \alpha_\sigma(v^*(\overline{\sigma\omega}z)) \ d\sigma \Big) d\omega \\ &=\int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega)u^*\xi(\sigma)\alpha_\omega(a) \alpha_{\omega\sigma }\big(\overline{\sigma\omega}z f(\overline{\sigma\omega}z)u \big) d\sigma d\omega \\ &\stackrel{\mathrm{(vi)}}{=} \int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega)u^* \xi(\sigma)\alpha_\omega(a) \overline{\sigma\omega}z f(\overline{\sigma\omega}z) \omega\sigma u \ d\sigma d\omega \\ &= z\int_{\mathbb{T}}\int_{\mathbb{T}} \xi(\sigma)u^*\alpha_\omega(a)u f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega\\ &\stackrel{\mathrm{(vii)}}{\approx}_{\!\!\frac{\varepsilon}{2}} z\int_{\mathbb{T}}\int_{\mathbb{T}} \xi(\sigma)\alpha_\omega(a) f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega. \end{align*} $$
By (iv), if in the above expression, we replace
![]() $\xi (\sigma )\alpha _\omega (a)$
by
$\xi (\sigma )\alpha _\omega (a)$
by
![]() $\xi (z)a$
, we obtain an element in A whose distance to
$\xi (z)a$
, we obtain an element in A whose distance to
![]() $(v\ast b \ast v^*)(z)$
is at most
$(v\ast b \ast v^*)(z)$
is at most
![]() $\varepsilon /2$
. Hence,
$\varepsilon /2$
. Hence,
 $$ \begin{align*} (v\ast b \ast v^*)(z)&\approx_{\varepsilon} z \xi(z)a\int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega \\ &= z b(z) \int_{\mathbb{T}} (f\ast f)(\overline{\sigma}z)\ d\sigma = z b(z)\|f\ast f\|_1\stackrel{\mathrm{(ii)}}{=} \widehat{\alpha}(b)(z).\end{align*} $$
$$ \begin{align*} (v\ast b \ast v^*)(z)&\approx_{\varepsilon} z \xi(z)a\int_{\mathbb{T}}\int_{\mathbb{T}} f(\omega) f(\overline{\sigma\omega}z) \ d\sigma d\omega \\ &= z b(z) \int_{\mathbb{T}} (f\ast f)(\overline{\sigma}z)\ d\sigma = z b(z)\|f\ast f\|_1\stackrel{\mathrm{(ii)}}{=} \widehat{\alpha}(b)(z).\end{align*} $$
We conclude that
as desired. This shows that
![]() $\widehat {\alpha }$
is approximately representable.
$\widehat {\alpha }$
is approximately representable.
Conversely, assume that
![]() $\widehat {\alpha }$
is approximately representable. Denote the left regular representation of G by
$\widehat {\alpha }$
is approximately representable. Denote the left regular representation of G by
![]() $\lambda \colon {\mathbb {T}}\to {\mathcal {U}}(L^2({\mathbb {T}}))$
. By Takai duality, there is a canonical equivariant identification
$\lambda \colon {\mathbb {T}}\to {\mathcal {U}}(L^2({\mathbb {T}}))$
. By Takai duality, there is a canonical equivariant identification
Let
![]() $p\in {\mathcal {K}}(L^2({\mathbb {T}}))$
be the projection onto the constant functions, and let
$p\in {\mathcal {K}}(L^2({\mathbb {T}}))$
be the projection onto the constant functions, and let
![]() $e\in M(A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}})$
be the projection corresponding to
$e\in M(A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}})$
be the projection corresponding to
![]() $1_A\otimes p$
under the identification in (2.3). Then e and p are
$1_A\otimes p$
under the identification in (2.3). Then e and p are
![]() ${\mathbb {T}}$
-invariant, and there is a canonical equivariant isomorphism
${\mathbb {T}}$
-invariant, and there is a canonical equivariant isomorphism
Let
![]() $u\in M(A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}})$
be the canonical unitary implementing
$u\in M(A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}})$
be the canonical unitary implementing
![]() $\widehat {\alpha }$
. Let
$\widehat {\alpha }$
. Let
![]() $F\subseteq A$
be a finite subset, and let
$F\subseteq A$
be a finite subset, and let
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $\delta>0$
such that whenever
$\delta>0$
such that whenever
![]() $x\in A$
satisfies
$x\in A$
satisfies
![]() $\|x^*x-1\|<\delta $
and
$\|x^*x-1\|<\delta $
and
![]() $\|xx^*-1\|<\delta $
, then there is
$\|xx^*-1\|<\delta $
, then there is
![]() $w\in {\mathcal {U}}(A)$
with
$w\in {\mathcal {U}}(A)$
with
![]() $\|w-x\|<\varepsilon /2$
. Set
$\|w-x\|<\varepsilon /2$
. Set
Let
![]() $F'\subseteq A\rtimes _\alpha {\mathbb {T}}$
be a finite subset and let
$F'\subseteq A\rtimes _\alpha {\mathbb {T}}$
be a finite subset and let
![]() $n\in {\mathbb {N}}$
such that any element in
$n\in {\mathbb {N}}$
such that any element in
![]() $F"$
is within
$F"$
is within
![]() $\varepsilon /2$
of the span of
$\varepsilon /2$
of the span of
![]() $\{bu^k\colon b\in F', -n\leq k\leq n\}$
. Using approximate representability of
$\{bu^k\colon b\in F', -n\leq k\leq n\}$
. Using approximate representability of
![]() $\widehat {\alpha }$
, let
$\widehat {\alpha }$
, let
![]() $v\in A\rtimes _\alpha {\mathbb {T}}$
be a contraction satisfying conditions (a), (b), (c), and (d) in Definition 2.6 for
$v\in A\rtimes _\alpha {\mathbb {T}}$
be a contraction satisfying conditions (a), (b), (c), and (d) in Definition 2.6 for
![]() $\varepsilon _0=\min \big \{\frac {\varepsilon }{26n^2|F'|},\delta \big \}$
and
$\varepsilon _0=\min \big \{\frac {\varepsilon }{26n^2|F'|},\delta \big \}$
and
![]() $F'$
. Set
$F'$
. Set
![]() $y=v^*u$
, which is a contraction in
$y=v^*u$
, which is a contraction in
![]() $A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}}$
. Then
$A\rtimes _\alpha {\mathbb {T}}\rtimes _{\widehat {\alpha }}{\mathbb {Z}}$
. Then
for all
![]() $z\in {\mathbb {T}}$
. Moreover, given
$z\in {\mathbb {T}}$
. Moreover, given
![]() $b\in F'$
and
$b\in F'$
and
![]() $k\in {\mathbb {Z}}$
with
$k\in {\mathbb {Z}}$
with
![]() $|k|\leq n$
, we have
$|k|\leq n$
, we have
 $$ \begin{align*} ybu^k&=v^*ubu^k=v^*\widehat{\alpha}(b)u^{k+1}\stackrel{\mathrm{(b)}}{\approx}_{\!\varepsilon_0} v^*\widehat{\alpha}(b)v^*vu^{k+1}\\ &\stackrel{\mathrm{(a)}}{\approx}_{\!\varepsilon_0} v^*\widehat{\alpha}(b)vv^*u^{k+1} \stackrel{\mathrm{(d)}}{\approx}_{\!\varepsilon_0} v^*vbv^*vv^*u^{k+1}\\ &\stackrel{\mathrm{(b)}}{\approx}_{\!2\varepsilon_0} bv^*u^{k+1} \stackrel{\mathrm{(c)}}{\approx}_{\!k\varepsilon_0}bu^kv^*u=bu^ky. \end{align*} $$
$$ \begin{align*} ybu^k&=v^*ubu^k=v^*\widehat{\alpha}(b)u^{k+1}\stackrel{\mathrm{(b)}}{\approx}_{\!\varepsilon_0} v^*\widehat{\alpha}(b)v^*vu^{k+1}\\ &\stackrel{\mathrm{(a)}}{\approx}_{\!\varepsilon_0} v^*\widehat{\alpha}(b)vv^*u^{k+1} \stackrel{\mathrm{(d)}}{\approx}_{\!\varepsilon_0} v^*vbv^*vv^*u^{k+1}\\ &\stackrel{\mathrm{(b)}}{\approx}_{\!2\varepsilon_0} bv^*u^{k+1} \stackrel{\mathrm{(c)}}{\approx}_{\!k\varepsilon_0}bu^kv^*u=bu^ky. \end{align*} $$
It follows from the choice of
![]() $F'$
, n and
$F'$
, n and
![]() $\varepsilon _0$
that
$\varepsilon _0$
that
for every
![]() $c\in F"$
. Set
$c\in F"$
. Set
![]() $x=eye$
, which we regard as an element in A. By (2.5), we have
$x=eye$
, which we regard as an element in A. By (2.5), we have
![]() $\alpha _z(x)=z x$
for all
$\alpha _z(x)=z x$
for all
![]() $z\in {\mathbb {T}}$
, since e is
$z\in {\mathbb {T}}$
, since e is
![]() ${\mathbb {T}}$
-invariant. For
${\mathbb {T}}$
-invariant. For
![]() $a\in F,$
we have
$a\in F,$
we have
since
![]() $a\otimes p$
belongs to
$a\otimes p$
belongs to
![]() $F"$
. Moreover,
$F"$
. Moreover,
![]() $\|x^*x-1\|=\|ey^*eye-e\|<\varepsilon _0\leq \delta $
, and similarly
$\|x^*x-1\|=\|ey^*eye-e\|<\varepsilon _0\leq \delta $
, and similarly
![]() $\|xx^*-1\|<\delta $
. By the choice of
$\|xx^*-1\|<\delta $
. By the choice of
![]() $\delta $
, there exists a unitary
$\delta $
, there exists a unitary
![]() $w\in A$
such that
$w\in A$
such that
![]() $\|w-x\|<\varepsilon /2$
. It is then straightforward to check that
$\|w-x\|<\varepsilon /2$
. It is then straightforward to check that
![]() $\|wa-aw\|<\varepsilon $
for all
$\|wa-aw\|<\varepsilon $
for all
![]() $a\in F$
and
$a\in F$
and
![]() $\max _{z\in {\mathbb {T}}}\|\alpha _z(w)-z w\|<\varepsilon /2$
. This shows that
$\max _{z\in {\mathbb {T}}}\|\alpha _z(w)-z w\|<\varepsilon /2$
. This shows that
![]() $\alpha $
has the Rokhlin property.
$\alpha $
has the Rokhlin property.
(2). Assume that
![]() $\beta $
is approximately representable. Let F be a finite subset of
$\beta $
is approximately representable. Let F be a finite subset of
![]() $A\rtimes _{\beta }{\mathbb {Z}}$
and let
$A\rtimes _{\beta }{\mathbb {Z}}$
and let
![]() $\varepsilon>0$
. Denote by u the canonical unitary in the crossed product. Since A and u generate
$\varepsilon>0$
. Denote by u the canonical unitary in the crossed product. Since A and u generate
![]() $A\rtimes _{\beta }{\mathbb {Z}}$
, one can assume that
$A\rtimes _{\beta }{\mathbb {Z}}$
, one can assume that
![]() $F=F'\cup \{u\}$
, where
$F=F'\cup \{u\}$
, where
![]() $F'$
is a finite subset of A. Using approximate representability for
$F'$
is a finite subset of A. Using approximate representability for
![]() $\beta $
, find
$\beta $
, find
![]() $v\in {\mathcal {U}}(A)$
with:
$v\in {\mathcal {U}}(A)$
with:
-
•
 $\|\beta (b)-vbv^*\|<\varepsilon $
for all
$\|\beta (b)-vbv^*\|<\varepsilon $
for all
 $b\in \beta (F')$
, and
$b\in \beta (F')$
, and -
•
 $\|\beta (v)-v\|<\varepsilon $
.
$\|\beta (v)-v\|<\varepsilon $
.
Set
![]() $w=v^*u$
, which is a unitary in
$w=v^*u$
, which is a unitary in
![]() $A\rtimes _\beta {\mathbb {Z}}$
. For
$A\rtimes _\beta {\mathbb {Z}}$
. For
![]() $b\in F',$
we have
$b\in F',$
we have
Moreover,
It follows that
![]() $\|wa-aw\|<\varepsilon $
for all
$\|wa-aw\|<\varepsilon $
for all
![]() $a\in F=F'\cup \{u\}$
. On the other hand,
$a\in F=F'\cup \{u\}$
. On the other hand,
for all
![]() $ z\in {\mathbb {T}}$
. Thus, w is the desired unitary, and
$ z\in {\mathbb {T}}$
. Thus, w is the desired unitary, and
![]() $\widehat {\beta }$
has the Rokhlin property.
$\widehat {\beta }$
has the Rokhlin property.
Conversely, assume that
![]() $\widehat {\beta }$
has the Rokhlin property. We continue to denote by u the canonical unitary in
$\widehat {\beta }$
has the Rokhlin property. We continue to denote by u the canonical unitary in
![]() $A\rtimes _\beta {\mathbb {Z}}$
that implements
$A\rtimes _\beta {\mathbb {Z}}$
that implements
![]() $\beta $
. Let
$\beta $
. Let
![]() $F\subseteq A$
be a finite subset and set
$F\subseteq A$
be a finite subset and set
![]() $F'=F\cup \{u\}\subseteq A\rtimes _\beta {\mathbb {Z}}$
. Use Proposition 2.2 to choose a unitary
$F'=F\cup \{u\}\subseteq A\rtimes _\beta {\mathbb {Z}}$
. Use Proposition 2.2 to choose a unitary
![]() $w\in {\mathcal {U}}(A\rtimes _\beta {\mathbb {Z}})$
such that:
$w\in {\mathcal {U}}(A\rtimes _\beta {\mathbb {Z}})$
such that:
-
•
 $\widehat {\beta }_ z(w)= z w$
for all
$\widehat {\beta }_ z(w)= z w$
for all
 $ z\in {\mathbb {T}}$
;
$ z\in {\mathbb {T}}$
; -
•
 $\|wb-bw\|=0$
for all
$\|wb-bw\|=0$
for all
 $b\in F'$
.
$b\in F'$
.
Set
![]() $v=uw^*\in A\rtimes _\beta {\mathbb {Z}}$
. Then the first condition above implies that
$v=uw^*\in A\rtimes _\beta {\mathbb {Z}}$
. Then the first condition above implies that
![]() $\widehat {\beta }_ z(v)=v$
for all
$\widehat {\beta }_ z(v)=v$
for all
![]() $ z\in {\mathbb {T}}$
, and hence the unitary v belongs to the fixed point algebra
$ z\in {\mathbb {T}}$
, and hence the unitary v belongs to the fixed point algebra
![]() $(A\rtimes _\beta {\mathbb {Z}})^{\widehat {\beta }}$
, which equals A by Proposition 7.8.9 in [Reference Pedersen34]. For
$(A\rtimes _\beta {\mathbb {Z}})^{\widehat {\beta }}$
, which equals A by Proposition 7.8.9 in [Reference Pedersen34]. For
![]() $a\in F$
, we have
$a\in F$
, we have
Moreover,
![]() $\|\beta (v)-v\|=\|u(uw^*)u^*-uw^*\|<\varepsilon $
, since
$\|\beta (v)-v\|=\|u(uw^*)u^*-uw^*\|<\varepsilon $
, since
![]() $u\in F'$
. It follows that v satisfies the conditions of Definition 2.6, so
$u\in F'$
. It follows that v satisfies the conditions of Definition 2.6, so
![]() $\beta $
is approximately representable.
$\beta $
is approximately representable.
Using Proposition 2.8, we show that for actions with the Rokhlin property, every ideal in the crossed product is induced by an invariant ideal of the algebra.
Proposition 2.9 Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
have the Rokhlin property. Then every ideal in
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
have the Rokhlin property. Then every ideal in
![]() $A^\alpha $
has the form
$A^\alpha $
has the form
![]() $I\cap A^\alpha $
, for some
$I\cap A^\alpha $
, for some
![]() ${\mathbb {T}}$
-invariant ideal I in A, and every ideal in
${\mathbb {T}}$
-invariant ideal I in A, and every ideal in
![]() $A\rtimes _\alpha {\mathbb {T}}$
has the form
$A\rtimes _\alpha {\mathbb {T}}$
has the form
![]() $I\rtimes _\alpha {\mathbb {T}}$
for some
$I\rtimes _\alpha {\mathbb {T}}$
for some
![]() ${\mathbb {T}}$
-invariant ideal I in A. In particular, if A is simple, then so are
${\mathbb {T}}$
-invariant ideal I in A. In particular, if A is simple, then so are
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $A\rtimes _\alpha {\mathbb {T}}$
.
$A\rtimes _\alpha {\mathbb {T}}$
.
Proof Since
![]() $A^\alpha \otimes {\mathcal {K}}(\ell ^2({\mathbb {Z}}))\cong A\rtimes _\alpha {\mathbb {T}}$
by Corollary 2.5, it is enough to show the statement for
$A^\alpha \otimes {\mathcal {K}}(\ell ^2({\mathbb {Z}}))\cong A\rtimes _\alpha {\mathbb {T}}$
by Corollary 2.5, it is enough to show the statement for
![]() $A^\alpha $
. We identify A with
$A^\alpha $
. We identify A with
![]() $A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
, where
$A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
, where
![]() $\check {\alpha }$
is the predual of
$\check {\alpha }$
is the predual of
![]() $\alpha $
; see Definition 2.4. Let J be an ideal in
$\alpha $
; see Definition 2.4. Let J be an ideal in
![]() $A^\alpha $
. Since
$A^\alpha $
. Since
![]() $\check {\alpha }$
is approximately inner by part (2) of Proposition 2.8, it follows that
$\check {\alpha }$
is approximately inner by part (2) of Proposition 2.8, it follows that
![]() $\check {\alpha }(J)=J$
. Hence
$\check {\alpha }(J)=J$
. Hence
![]() $I=J\rtimes _{\check {\alpha }}{\mathbb {Z}}$
is canonically an ideal in A satisfying
$I=J\rtimes _{\check {\alpha }}{\mathbb {Z}}$
is canonically an ideal in A satisfying
![]() $I\cap A^\alpha =J$
, as desired.
$I\cap A^\alpha =J$
, as desired.
3 K-theoretic obstructions to the Rokhlin property
In this section, we study the K-theory of
![]() $C^*$
-algebras that admit circle actions with the Rokhlin property. First, we show that the canonical inclusion
$C^*$
-algebras that admit circle actions with the Rokhlin property. First, we show that the canonical inclusion
![]() $A^\alpha \to A$
induces an injective order-embedding
$A^\alpha \to A$
induces an injective order-embedding
![]() $K_\ast (\iota )\colon K_\ast (A^\alpha )\to K_\ast (A)$
(see Proposition 3.1). Moreover, the quotient of
$K_\ast (\iota )\colon K_\ast (A^\alpha )\to K_\ast (A)$
(see Proposition 3.1). Moreover, the quotient of
![]() $K_\ast (A)$
by
$K_\ast (A)$
by
![]() $K_\ast (A^\alpha )$
can be canonically identified with
$K_\ast (A^\alpha )$
can be canonically identified with
![]() $K_\ast (SA^\alpha )$
, and the induced extension
$K_\ast (SA^\alpha )$
, and the induced extension
is pure (see Definition 3.2 and Theorem 3.3).
In the following proposition, we will use the fact that if
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
has the Rokhlin property, then so does its n-amplification
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
has the Rokhlin property, then so does its n-amplification
![]() $\alpha \otimes {\mathrm {id}}_{M_n}\colon {\mathbb {T}} \to {\mathrm {Aut}}(M_n(A))$
for every
$\alpha \otimes {\mathrm {id}}_{M_n}\colon {\mathbb {T}} \to {\mathrm {Aut}}(M_n(A))$
for every
![]() $n\in {\mathbb {N}}$
, and that
$n\in {\mathbb {N}}$
, and that
![]() $M_n(A)^{\alpha \otimes {\mathrm {id}}_{M_n}}=M_n(A^\alpha )$
.
$M_n(A)^{\alpha \otimes {\mathrm {id}}_{M_n}}=M_n(A^\alpha )$
.
Proposition 3.1 Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property, and let
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property, and let
![]() $\iota \colon A^\alpha \hookrightarrow A$
denote the canonical inclusion. Then
$\iota \colon A^\alpha \hookrightarrow A$
denote the canonical inclusion. Then
![]() $K_0(\iota )$
and
$K_0(\iota )$
and
![]() $K_1(\iota )$
are injective. Moreover, for
$K_1(\iota )$
are injective. Moreover, for
![]() $x,y\in K_0(A^\alpha ),$
we have
$x,y\in K_0(A^\alpha ),$
we have
![]() $K_0(\iota )(x)\leq K_0(\iota )(y)$
in
$K_0(\iota )(x)\leq K_0(\iota )(y)$
in
![]() $K_0(A)$
if and only if
$K_0(A)$
if and only if
![]() $x\leq y$
in
$x\leq y$
in
![]() $K_0(A^\alpha )$
.
$K_0(A^\alpha )$
.
Proof Consider the Pimsner–Voiculescu exact sequence associated with the predual automorphism
![]() $\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
of
$\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
of
![]() $\alpha $
(Definition 2.4):
$\alpha $
(Definition 2.4):

Since
![]() $\check {\alpha }$
is approximately inner by part (2) of Proposition 2.8, we get
$\check {\alpha }$
is approximately inner by part (2) of Proposition 2.8, we get
![]() $K_\ast (\check {\alpha })=1$
and thus
$K_\ast (\check {\alpha })=1$
and thus
![]() $K_\ast (\iota )$
is injective.
$K_\ast (\iota )$
is injective.
We turn to the last part of the statement. Let
![]() $x,y\in K_0(A^\alpha )$
, and assume that
$x,y\in K_0(A^\alpha )$
, and assume that
![]() $K_0(\iota )(x)\leq K_0(\iota )(y)$
. Set
$K_0(\iota )(x)\leq K_0(\iota )(y)$
. Set
![]() $z=y-x$
, so that
$z=y-x$
, so that
![]() $K_0(\iota )(z)\geq 0$
in
$K_0(\iota )(z)\geq 0$
in
![]() $K_0(A)$
. Find projections
$K_0(A)$
. Find projections
![]() $p,q\in \bigcup _{m\in {\mathbb {N}}}M_m(A^\alpha )$
with
$p,q\in \bigcup _{m\in {\mathbb {N}}}M_m(A^\alpha )$
with
![]() $z=[p]-[q]$
in
$z=[p]-[q]$
in
![]() $K_0(A^\alpha )$
, and let
$K_0(A^\alpha )$
, and let
![]() $e\in \bigcup _{m\in {\mathbb {N}}}M_m(A)$
satisfy
$e\in \bigcup _{m\in {\mathbb {N}}}M_m(A)$
satisfy
![]() $K_0(\iota )(z)=[e]$
in
$K_0(\iota )(z)=[e]$
in
![]() $K_0(A)$
. Then
$K_0(A)$
. Then
![]() $[p]=[e]+[q]$
in
$[p]=[e]+[q]$
in
![]() $K_0(A)$
. By increasing the matrix sizes, we may assume that there exist
$K_0(A)$
. By increasing the matrix sizes, we may assume that there exist
![]() $k,n\in {\mathbb {N}}$
such that:
$k,n\in {\mathbb {N}}$
such that:
-
• p and q belong to
 $M_n(A^\alpha )$
;
$M_n(A^\alpha )$
; -
• e belongs to
 $M_n(A)$
;
$M_n(A)$
; -
• e is orthogonal to
 $q\oplus 1_k$
;
$q\oplus 1_k$
; -
•
 $p\oplus 1_k$
is Murray–von Neumann equivalent to
$p\oplus 1_k$
is Murray–von Neumann equivalent to
 $(e+q)\oplus 1_k$
in
$(e+q)\oplus 1_k$
in
 $M_{n+k}(A)$
.
$M_{n+k}(A)$
.
Note that
![]() $z=[p\oplus 1_k]-[q\oplus 1_k]$
. Without loss of generality, upon replacing p and q with
$z=[p\oplus 1_k]-[q\oplus 1_k]$
. Without loss of generality, upon replacing p and q with
![]() $p\oplus 1_k$
and
$p\oplus 1_k$
and
![]() $q\oplus 1_k$
, respectively, and n with
$q\oplus 1_k$
, respectively, and n with
![]() $n+k$
, we may moreover assume that:
$n+k$
, we may moreover assume that:
-
• e is orthogonal to q;
-
• p is Murray–von Neumann equivalent to
 $e+q$
in
$e+q$
in
 $M_n(A)$
.
$M_n(A)$
.
Set
![]() $\alpha ^{(n)}=\alpha \otimes {\mathrm {id}}_{M_n}$
, which has the Rokhlin property. Let
$\alpha ^{(n)}=\alpha \otimes {\mathrm {id}}_{M_n}$
, which has the Rokhlin property. Let
![]() $s\in M_n(A)$
be a partial isometry satisfying
$s\in M_n(A)$
be a partial isometry satisfying
![]() $s^*s=p$
and
$s^*s=p$
and
![]() $ss^*=e+q$
. For
$ss^*=e+q$
. For
![]() $\varepsilon =1/12$
, let
$\varepsilon =1/12$
, let
![]() $\delta>0$
such that whenever B is a
$\delta>0$
such that whenever B is a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $a\in B_{\mathrm {sa}}$
satisfies
$a\in B_{\mathrm {sa}}$
satisfies
![]() $\|a^2-a\|<\delta $
, then there exists a projection
$\|a^2-a\|<\delta $
, then there exists a projection
![]() $r\in B$
with
$r\in B$
with
![]() $\|r-a\|<\varepsilon $
. Set
$\|r-a\|<\varepsilon $
. Set
![]() $\varepsilon _0=\min \{\varepsilon ,\delta /5\}$
, and let
$\varepsilon _0=\min \{\varepsilon ,\delta /5\}$
, and let
![]() $\sigma \colon M_n(A)\to M_n(A^\alpha )$
be a unital completely positive map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
$\sigma \colon M_n(A)\to M_n(A^\alpha )$
be a unital completely positive map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
![]() $\varepsilon _0$
,
$\varepsilon _0$
,
![]() $F_1=\{p,q,e,s,s^*\}$
and
$F_1=\{p,q,e,s,s^*\}$
and
![]() $F_2=\{p,q\}$
. Set
$F_2=\{p,q\}$
. Set
![]() $t=\sigma (s)$
and
$t=\sigma (s)$
and
![]() $f=\sigma (e)$
. Then
$f=\sigma (e)$
. Then
so
![]() $\|t^*t-p\|<2\varepsilon _0$
. In particular,
$\|t^*t-p\|<2\varepsilon _0$
. In particular,
![]() $(1-q)f\approx _{2\varepsilon _0} f$
and hence
$(1-q)f\approx _{2\varepsilon _0} f$
and hence
![]() $\|qf\|<2\varepsilon _0$
. Similarly,
$\|qf\|<2\varepsilon _0$
. Similarly,
![]() $\|fq\|<2\varepsilon _0$
.
$\|fq\|<2\varepsilon _0$
.
Set
![]() $a=(1-q)f(1-q)$
. Then
$a=(1-q)f(1-q)$
. Then
![]() $a=a^*$
and
$a=a^*$
and
![]() $\|a-f\|\leq 4\varepsilon _0$
. Moreover,
$\|a-f\|\leq 4\varepsilon _0$
. Moreover,
so
![]() $\|a^2-a\|\leq 4\varepsilon _0<\delta $
. By the choice of
$\|a^2-a\|\leq 4\varepsilon _0<\delta $
. By the choice of
![]() $\delta $
applied to
$\delta $
applied to
![]() $B=(1-q)M_n(A^\alpha )(1-q)$
, there exists a projection
$B=(1-q)M_n(A^\alpha )(1-q)$
, there exists a projection
![]() $r\in M_n(A^\alpha )$
with
$r\in M_n(A^\alpha )$
with
![]() $\|r-a\|<\varepsilon $
and
$\|r-a\|<\varepsilon $
and
![]() $rq=0$
.
$rq=0$
.
Set
![]() $x=(q+r)tp\in M_n(A^\alpha )$
. Then
$x=(q+r)tp\in M_n(A^\alpha )$
. Then
 $$ \begin{align*} x^*x&=pt^*(q+r)tp\approx_\varepsilon pt^*(q+a)tp\\ &\approx_{4\varepsilon_0}pt^*(q+f)tp \approx_{2\varepsilon_0}pt^*tt^*tp\\ &\approx_{2\varepsilon_0}p^4=p, \end{align*} $$
$$ \begin{align*} x^*x&=pt^*(q+r)tp\approx_\varepsilon pt^*(q+a)tp\\ &\approx_{4\varepsilon_0}pt^*(q+f)tp \approx_{2\varepsilon_0}pt^*tt^*tp\\ &\approx_{2\varepsilon_0}p^4=p, \end{align*} $$
so
![]() $\|x^*x-p\|\leq 8\varepsilon _0+\varepsilon <1$
. Similarly, we have
$\|x^*x-p\|\leq 8\varepsilon _0+\varepsilon <1$
. Similarly, we have
 $$ \begin{align*} xx^*&=(q+r)tpt^*(q+r)\approx_{2\varepsilon_0} (q+r)tt^*tt^*(q+r)\\ &\approx_{4\varepsilon_0}(q+r)(q+f)(q+f)(q+r) \approx_{4\varepsilon_0+\varepsilon}(q+r)^4=q+r, \end{align*} $$
$$ \begin{align*} xx^*&=(q+r)tpt^*(q+r)\approx_{2\varepsilon_0} (q+r)tt^*tt^*(q+r)\\ &\approx_{4\varepsilon_0}(q+r)(q+f)(q+f)(q+r) \approx_{4\varepsilon_0+\varepsilon}(q+r)^4=q+r, \end{align*} $$
so
![]() $\|xx^*-(q+r)\|\leq 10\varepsilon _0+\varepsilon <1$
. Since
$\|xx^*-(q+r)\|\leq 10\varepsilon _0+\varepsilon <1$
. Since
![]() $x=(q+r)xp$
, it follows from Lemma 2.5.3 in [Reference Lin25] that there exists a partial isometry
$x=(q+r)xp$
, it follows from Lemma 2.5.3 in [Reference Lin25] that there exists a partial isometry
![]() $v\in M_n(A^\alpha )$
such that
$v\in M_n(A^\alpha )$
such that
![]() $v^*v=p$
and
$v^*v=p$
and
![]() $vv^*=q+r$
. It follows that
$vv^*=q+r$
. It follows that
![]() $[p]=[q]+[r]$
in
$[p]=[q]+[r]$
in
![]() $K_0(A^\alpha )$
, and thus
$K_0(A^\alpha )$
, and thus
![]() $z=[p]-[q]$
is positive in
$z=[p]-[q]$
is positive in
![]() $K_0(A^\alpha )$
, as desired.
$K_0(A^\alpha )$
, as desired.
Next, we recall the definition of a pure subgroup and a pure extension.
Definition 3.2 Let G be an abelian group, and let H be a subgroup. We say that H is pure if
![]() $nH=nG\cap H$
for all
$nH=nG\cap H$
for all
![]() $n\in {\mathbb {N}}$
. In other words, for every
$n\in {\mathbb {N}}$
. In other words, for every
![]() $h\in H$
and
$h\in H$
and
![]() $n\in {\mathbb {N}}$
, if there exists
$n\in {\mathbb {N}}$
, if there exists
![]() $g\in G$
with
$g\in G$
with
![]() $ng=h,$
then there exists
$ng=h,$
then there exists
![]() $h'\in H$
with
$h'\in H$
with
![]() $nh'=h$
.
$nh'=h$
.
An extension
![]() $0\to H\to G\to Q\to 0$
is said to be pure if H is pure in G.
$0\to H\to G\to Q\to 0$
is said to be pure if H is pure in G.
The notion of a pure subgroup generalizes that of a direct summand. For example, the torsion subgroup of any abelian group is always a pure subgroup, although it is not always a direct summand. If G is finitely generated, then any pure subgroup is automatically a direct summand. On the other hand, there exist pure subgroups which are finitely generated, yet not a direct summand (despite being direct summands in every finitely generated subgroup that contains them).
In the following theorem, note that part (3) does not follow from part (2) since in (3) we only make assumptions about one of the K-groups of A, and not both. Also, if we assume that A satisfies the UCT, then part (1) admits an easier proof: by the universal multicoefficient theorem, the 6-term Pimsner–Voiculescu exact sequence decomposes into two pure extensions if and only if its boundary map vanishes once tensored with
![]() $\mathcal {O}_n$
for
$\mathcal {O}_n$
for
![]() $n=2,3,\ldots ,\infty $
. That said maps vanish follows from Proposition 3.1, since the dynamical system
$n=2,3,\ldots ,\infty $
. That said maps vanish follows from Proposition 3.1, since the dynamical system
![]() $(A\otimes \mathcal {O}_n,\alpha \otimes {\mathrm {id}}_{\mathcal {O}_n})$
has the Rokhlin property for all
$(A\otimes \mathcal {O}_n,\alpha \otimes {\mathrm {id}}_{\mathcal {O}_n})$
has the Rokhlin property for all
![]() $n=2,3,\ldots ,\infty $
. We thank the anonymous referee for providing us with this argument.
$n=2,3,\ldots ,\infty $
. We thank the anonymous referee for providing us with this argument.
Theorem 3.3 Let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action on a unital
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action on a unital
![]() $C^*$
-algebra A with the Rokhlin property. Denote by
$C^*$
-algebra A with the Rokhlin property. Denote by
![]() $\iota \colon A^\alpha \to A$
the canonical inclusion.
$\iota \colon A^\alpha \to A$
the canonical inclusion.
-
1. There is a canonical class
 ${\mathrm {Ext}}_\ast (\alpha )=({\mathrm {Ext}}_0(\alpha ),{\mathrm {Ext}}_1(\alpha ))$
, where
${\mathrm {Ext}}_\ast (\alpha )=({\mathrm {Ext}}_0(\alpha ),{\mathrm {Ext}}_1(\alpha ))$
, where
 ${\mathrm {Ext}}_j(\alpha )\in {\mathrm {Ext}}(K_j(SA^\alpha ),K_j(A^\alpha ))$
is the pure extension
${\mathrm {Ext}}_j(\alpha )\in {\mathrm {Ext}}(K_j(SA^\alpha ),K_j(A^\alpha ))$
is the pure extension 
-
2. If both
 $K_0(A)$
and
$K_0(A)$
and
 $K_1(A)$
are (possibly infinite) direct sums of cyclic groups, then there are isomorphisms such that
$K_1(A)$
are (possibly infinite) direct sums of cyclic groups, then there are isomorphisms such that $$\begin{align*}K_0(A)\cong K_1(A)\cong K_0(A^\alpha)\oplus K_1(A^\alpha)\end{align*}$$
$$\begin{align*}K_0(A)\cong K_1(A)\cong K_0(A^\alpha)\oplus K_1(A^\alpha)\end{align*}$$
 $[1_A]\in K_0(A)$
is sent to
$[1_A]\in K_0(A)$
is sent to
 $([1_{A^\alpha }],0)\in K_0(A^\alpha )\oplus K_1(A^\alpha )$
.
$([1_{A^\alpha }],0)\in K_0(A^\alpha )\oplus K_1(A^\alpha )$
.
-
3. If at least one of
 $K_0(A)$
or
$K_0(A)$
or
 $K_1(A)$
is finitely generated, then there are isomorphisms as in (2).
$K_1(A)$
is finitely generated, then there are isomorphisms as in (2).
Proof (1). Arguing as in the beginning of the proof of Proposition 3.1, we deduce that the Pimsner–Voiculescu exact sequence associated with
![]() $\check {\alpha }$
splits into the short exact sequence
$\check {\alpha }$
splits into the short exact sequence
We claim that the extension is pure. By taking considering the tensor product of A with any unital
![]() $C^*$
-algebra which is KK-equivalent to
$C^*$
-algebra which is KK-equivalent to
![]() $C_0(\mathbb {R})$
, endowed with the trivial action of
$C_0(\mathbb {R})$
, endowed with the trivial action of
![]() $\mathbb {T}$
, it follows that it suffices to prove that
$\mathbb {T}$
, it follows that it suffices to prove that
![]() $K_0(A^\alpha )$
is a pure subgroup of
$K_0(A^\alpha )$
is a pure subgroup of
![]() $K_0(A)$
. Let
$K_0(A)$
. Let
![]() $x\in K_0(A^\alpha )$
, let
$x\in K_0(A^\alpha )$
, let
![]() $k\in {\mathbb {N}}$
, and let
$k\in {\mathbb {N}}$
, and let
![]() $y\in K_0(A)$
, and suppose that
$y\in K_0(A)$
, and suppose that
![]() $ky=K_0(\iota )(x)$
. Find projections
$ky=K_0(\iota )(x)$
. Find projections
![]() $p_x,q_x\in \bigcup _{m\in {\mathbb {N}}} M_m(A^\alpha )$
and
$p_x,q_x\in \bigcup _{m\in {\mathbb {N}}} M_m(A^\alpha )$
and
![]() $p_y,q_y\in \bigcup _{m\in {\mathbb {N}}} M_m(A)$
such that
$p_y,q_y\in \bigcup _{m\in {\mathbb {N}}} M_m(A)$
such that
![]() $x=[p_x]-[q_x]$
and
$x=[p_x]-[q_x]$
and
![]() $y=[p_y]-[q_y]$
. It follows that
$y=[p_y]-[q_y]$
. It follows that
![]() $k[p_y]+[q_x]=[p_x]+k[q_y]$
in
$k[p_y]+[q_x]=[p_x]+k[q_y]$
in
![]() $K_0(A)$
. Without loss of generality, we may assume that there is
$K_0(A)$
. Without loss of generality, we may assume that there is
![]() $n\in {\mathbb {N}}$
such that:
$n\in {\mathbb {N}}$
such that:
-
•
 $p_x,q_x$
to
$p_x,q_x$
to
 $M_n(A)^\alpha $
and
$M_n(A)^\alpha $
and
 $p_y,q_y$
belong to
$p_y,q_y$
belong to
 $M_n(A)$
;
$M_n(A)$
; -
•
 $p_x$
is orthogonal to
$p_x$
is orthogonal to
 $q_y$
and
$q_y$
and
 $p_y$
is orthogonal to
$p_y$
is orthogonal to
 $q_x$
;
$q_x$
; -
• there exists
 $s\in M_{nk}(A)$
with
$s\in M_{nk}(A)$
with  $$ \begin{align*} s^*s=\left( \begin{array}{cccc} q_x+p_y & & & \\ & p_y & & \\ & & \ddots & \\ & & & p_y \\ \end{array} \right) \ \ \mbox{ and } \ \ ss^*=\left( \begin{array}{cccc} p_x+q_y & & & \\ & q_y & & \\ & & \ddots & \\ & & & q_y \\ \end{array} \right).\end{align*} $$
$$ \begin{align*} s^*s=\left( \begin{array}{cccc} q_x+p_y & & & \\ & p_y & & \\ & & \ddots & \\ & & & p_y \\ \end{array} \right) \ \ \mbox{ and } \ \ ss^*=\left( \begin{array}{cccc} p_x+q_y & & & \\ & q_y & & \\ & & \ddots & \\ & & & q_y \\ \end{array} \right).\end{align*} $$
Note that
![]() $\alpha ^{(nk)}\colon {\mathbb {T}}\to {\mathrm {Aut}}(M_{nk}(A))$
has the Rokhlin property. For
$\alpha ^{(nk)}\colon {\mathbb {T}}\to {\mathrm {Aut}}(M_{nk}(A))$
has the Rokhlin property. For
![]() $\varepsilon =1/12$
, let
$\varepsilon =1/12$
, let
![]() $\delta>0$
such that whenever B is a
$\delta>0$
such that whenever B is a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $a\in B$
is a self-adjoint element satisfying
$a\in B$
is a self-adjoint element satisfying
![]() $\|a^2-a\|<\delta $
, then there exists a projection
$\|a^2-a\|<\delta $
, then there exists a projection
![]() $r\in B$
with
$r\in B$
with
![]() $\|r-a\|<\varepsilon $
. Set
$\|r-a\|<\varepsilon $
. Set
![]() $\varepsilon _0=\min \{\varepsilon ,\delta /10\}$
, and let
$\varepsilon _0=\min \{\varepsilon ,\delta /10\}$
, and let
![]() $\sigma \colon M_{nk}(A)\to M_{nk}(A^\alpha )$
be a unital completely positive map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
$\sigma \colon M_{nk}(A)\to M_{nk}(A^\alpha )$
be a unital completely positive map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
![]() $\varepsilon _0$
,
$\varepsilon _0$
,
![]() $F_1=\{p_x,q_x,p_y,q_y,s,s^*\}$
and
$F_1=\{p_x,q_x,p_y,q_y,s,s^*\}$
and
![]() $F_2=\{p_x,q_x\}$
. Then
$F_2=\{p_x,q_x\}$
. Then
![]() $\|\sigma (p_x)-p_x\|<\varepsilon $
and
$\|\sigma (p_x)-p_x\|<\varepsilon $
and
![]() $\|\sigma (q_x)-q_x\|<\varepsilon $
.
$\|\sigma (q_x)-q_x\|<\varepsilon $
.
Set
![]() $e_y=\sigma (p_y)$
and
$e_y=\sigma (p_y)$
and
![]() $f_y=\sigma (q_y)$
, which are self-adjoint contractions in
$f_y=\sigma (q_y)$
, which are self-adjoint contractions in
![]() $M_{nk}(A^\alpha )$
satisfying
$M_{nk}(A^\alpha )$
satisfying
![]() $\|e_y^2-e_y\|<2\varepsilon _0$
and
$\|e_y^2-e_y\|<2\varepsilon _0$
and
![]() $\|f_y^2-f_y\|<2\varepsilon _0.$
Set
$\|f_y^2-f_y\|<2\varepsilon _0.$
Set
![]() $t=\sigma (s)$
. Then
$t=\sigma (s)$
. Then
Set
![]() $a=(1-p_x)f_y(1-p_x)$
and
$a=(1-p_x)f_y(1-p_x)$
and
![]() $b=(1-q_x)e_y(1-q_x)$
, which are self-adjoint elements in the corners of
$b=(1-q_x)e_y(1-q_x)$
, which are self-adjoint elements in the corners of
![]() $M_{nk}(A^\alpha )$
by
$M_{nk}(A^\alpha )$
by
![]() $1-p_x$
and
$1-p_x$
and
![]() $1-q_x$
, respectively. Moreover,
$1-q_x$
, respectively. Moreover,
![]() $\|a-f_y\|\leq 4\varepsilon _0$
and
$\|a-f_y\|\leq 4\varepsilon _0$
and
![]() $\|b-e_y\|\leq 4\varepsilon _0$
. On the other hand,
$\|b-e_y\|\leq 4\varepsilon _0$
. On the other hand,
 $$ \begin{align*}a^2&=(1-p_x)f_y(1-p_x)f_y(1-p_x)\\ &\approx_{2\varepsilon_0}(1-p_x)f_y^2(1-p_x)\\ &\approx_{2\varepsilon_0}(1-p_x)f_y(1-p_x)=a,\end{align*} $$
$$ \begin{align*}a^2&=(1-p_x)f_y(1-p_x)f_y(1-p_x)\\ &\approx_{2\varepsilon_0}(1-p_x)f_y^2(1-p_x)\\ &\approx_{2\varepsilon_0}(1-p_x)f_y(1-p_x)=a,\end{align*} $$
so
![]() $\|a^2-a\|<4\varepsilon _0<\delta $
. Similarly, we have
$\|a^2-a\|<4\varepsilon _0<\delta $
. Similarly, we have
![]() $\|b^2-b\|<\delta $
. Using the definition of
$\|b^2-b\|<\delta $
. Using the definition of
![]() $\delta $
with
$\delta $
with
![]() $B=(1-p_x)M_{nk}(A^\alpha )(1-p_x)$
, there exits a projection
$B=(1-p_x)M_{nk}(A^\alpha )(1-p_x)$
, there exits a projection
![]() $\widetilde {q}_y \in M_{nk}(A^\alpha )$
satisfying
$\widetilde {q}_y \in M_{nk}(A^\alpha )$
satisfying
![]() $\|\widetilde {q}_y-a\|<\varepsilon $
and
$\|\widetilde {q}_y-a\|<\varepsilon $
and
![]() $p_x\widetilde {q}_y=0$
. Similarly, there exits a projection
$p_x\widetilde {q}_y=0$
. Similarly, there exits a projection
![]() $\widetilde {p}_y \in M_{nk}(A^\alpha )$
satisfying
$\widetilde {p}_y \in M_{nk}(A^\alpha )$
satisfying
![]() $\|\widetilde {p}_y-b\|<\varepsilon $
and
$\|\widetilde {p}_y-b\|<\varepsilon $
and
![]() $\widetilde {p}_yq_x=0$
. Set
$\widetilde {p}_yq_x=0$
. Set
which belongs to
![]() $M_{nk}(A^\alpha )$
. One checks that
$M_{nk}(A^\alpha )$
. One checks that
![]() $\|r^*r-{\mathrm {diag}}(q_x+\widetilde {p}_y,\widetilde {p}_y,\ldots ,\widetilde {p}_y)\|<1$
, and that
$\|r^*r-{\mathrm {diag}}(q_x+\widetilde {p}_y,\widetilde {p}_y,\ldots ,\widetilde {p}_y)\|<1$
, and that
![]() $\|r^*r-{\mathrm {diag}}(p_x+\widetilde {q}_y,\widetilde {q}_y,\ldots ,\widetilde {q}_y)\|<1$
. By Lemma 2.5.3 in [Reference Lin25], there exists a partial isometry
$\|r^*r-{\mathrm {diag}}(p_x+\widetilde {q}_y,\widetilde {q}_y,\ldots ,\widetilde {q}_y)\|<1$
. By Lemma 2.5.3 in [Reference Lin25], there exists a partial isometry
![]() $w\in M_{nk}(A^\alpha )$
such that
$w\in M_{nk}(A^\alpha )$
such that
 $$\begin{align*}w^*w=\left( \begin{array}{cccc} q_x+\widetilde{p}_y & & & \\ & \widetilde{p}_y & & \\ & & \ddots & \\ & & & \widetilde{p}_y \\ \end{array} \right) \ \mbox{ and } \ ww^*= \left( \begin{array}{cccc} p_y+\widetilde{q}_y & & & \\ & \widetilde{q}_y & & \\ & & \ddots & \\ & & & \widetilde{q}_y \\ \end{array} \right).\end{align*}$$
$$\begin{align*}w^*w=\left( \begin{array}{cccc} q_x+\widetilde{p}_y & & & \\ & \widetilde{p}_y & & \\ & & \ddots & \\ & & & \widetilde{p}_y \\ \end{array} \right) \ \mbox{ and } \ ww^*= \left( \begin{array}{cccc} p_y+\widetilde{q}_y & & & \\ & \widetilde{q}_y & & \\ & & \ddots & \\ & & & \widetilde{q}_y \\ \end{array} \right).\end{align*}$$
It follows that
![]() $[p_x]+k[\widetilde {q}_y]=k[\widetilde {p}_y]+[p_y]$
in
$[p_x]+k[\widetilde {q}_y]=k[\widetilde {p}_y]+[p_y]$
in
![]() $K_0(A^\alpha )$
. With
$K_0(A^\alpha )$
. With
![]() $z=[\widetilde {q}_x]-[\widetilde {q}_y]\in K_0(A^\alpha )$
, we have
$z=[\widetilde {q}_x]-[\widetilde {q}_y]\in K_0(A^\alpha )$
, we have
![]() $kz=x$
, as desired.
$kz=x$
, as desired.
(2). The displayed isomorphisms follow from Proposition 5.4 in [Reference Schochet40]. Since parts of the proposition are left as an exercise, and since we need to show that the isomorphism is compatible with the classes of the unit, we give a brief argument here for the existence of an isomorphism
![]() $K_0(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
sending
$K_0(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
sending
![]() $[1_A]$
to
$[1_A]$
to
![]() $([1_{A^\alpha }],0)$
. (The argument for
$([1_{A^\alpha }],0)$
. (The argument for
![]() $K_1(A)$
is identical because the assumptions are symmetric.) Abbreviate
$K_1(A)$
is identical because the assumptions are symmetric.) Abbreviate
![]() $K_j(A)$
to
$K_j(A)$
to
![]() $K_j$
, and
$K_j$
, and
![]() $K_j(A^\alpha )$
to
$K_j(A^\alpha )$
to
![]() $K_j^\alpha $
, for
$K_j^\alpha $
, for
![]() $j=0,1$
. It is a standard result in group theory, usually attributed to Kulikov, that subgroups of direct sums of cyclic groups are again direct sums of cyclic groups; see Theorem 18.1 in [Reference Fuchs6]. Since
$j=0,1$
. It is a standard result in group theory, usually attributed to Kulikov, that subgroups of direct sums of cyclic groups are again direct sums of cyclic groups; see Theorem 18.1 in [Reference Fuchs6]. Since
![]() $K_1$
is a direct sum of cyclic groups, we deduce that the same is true for
$K_1$
is a direct sum of cyclic groups, we deduce that the same is true for
![]() $K_1^\alpha $
.
$K_1^\alpha $
.
By part (1) of this theorem, there is a canonical quotient map
![]() $\pi \colon K_0\to K_1^\alpha $
whose kernel is
$\pi \colon K_0\to K_1^\alpha $
whose kernel is
![]() $K_0^\alpha $
. Choose a presentation
$K_0^\alpha $
. Choose a presentation
![]() $K_1^\alpha \cong \bigoplus _{s\in S}C_s$
, where each
$K_1^\alpha \cong \bigoplus _{s\in S}C_s$
, where each
![]() $C_s$
is a cyclic group with generator
$C_s$
is a cyclic group with generator
![]() $x_s$
. In particular,
$x_s$
. In particular,
![]() $\{x_s\colon s\in S\}$
generates
$\{x_s\colon s\in S\}$
generates
![]() $K_1^\alpha $
. Let
$K_1^\alpha $
. Let
![]() $s\in S$
. If
$s\in S$
. If
![]() $x_s$
has infinite order in
$x_s$
has infinite order in
![]() $K_1^\alpha $
, we let
$K_1^\alpha $
, we let
![]() $y_s\in K_0$
be any group element (necessarily of infinite order) satisfying
$y_s\in K_0$
be any group element (necessarily of infinite order) satisfying
![]() $\pi (y_s)=x_s$
. If
$\pi (y_s)=x_s$
. If
![]() $x_s$
has order
$x_s$
has order
![]() $n<\infty $
, let
$n<\infty $
, let
![]() $z_s\in K_0$
be any lift of
$z_s\in K_0$
be any lift of
![]() $x_s$
, and note that
$x_s$
, and note that
![]() $nz_s$
belongs to
$nz_s$
belongs to
![]() $K_0^\alpha $
, which is a pure subgroup of
$K_0^\alpha $
, which is a pure subgroup of
![]() $K_0$
. Hence, there exists
$K_0$
. Hence, there exists
![]() $k_s\in K_0^\alpha $
with
$k_s\in K_0^\alpha $
with
![]() $nk_s=nz_s$
, and we set
$nk_s=nz_s$
, and we set
![]() $y_s=z_s-k_s$
, which also lifts
$y_s=z_s-k_s$
, which also lifts
![]() $x_s$
.
$x_s$
.
Let L be the subgroup of
![]() $K_0$
generated by
$K_0$
generated by
![]() $\{y_s\colon s\in S\}$
, which is mapped isomorphically onto
$\{y_s\colon s\in S\}$
, which is mapped isomorphically onto
![]() $K_1^\alpha $
via
$K_1^\alpha $
via
![]() $\pi $
. In particular,
$\pi $
. In particular,
![]() $K_0^\alpha \cap L=\{0\}$
and
$K_0^\alpha \cap L=\{0\}$
and
![]() $K_0^\alpha +L=K_0$
. (Equivalently, L defines a splitting for the quotient map
$K_0^\alpha +L=K_0$
. (Equivalently, L defines a splitting for the quotient map
![]() $\pi $
.) We deduce that the extension
$\pi $
.) We deduce that the extension
![]() $0\to K_0^\alpha \to K_0\to K_1^\alpha \to 0$
splits, and thus
$0\to K_0^\alpha \to K_0\to K_1^\alpha \to 0$
splits, and thus
![]() $K_0\cong K_0^\alpha \oplus K_1^\alpha $
. The isomorphism can be clearly chosen to send
$K_0\cong K_0^\alpha \oplus K_1^\alpha $
. The isomorphism can be clearly chosen to send
![]() $[1_A]\in K_0$
to
$[1_A]\in K_0$
to
![]() $[1_{A^\alpha }]\in K_0^\alpha $
.
$[1_{A^\alpha }]\in K_0^\alpha $
.
(3). Assume that
![]() $K_1(A)$
is finitely generated (and in particular a direct sum of cyclic groups). Hence,
$K_1(A)$
is finitely generated (and in particular a direct sum of cyclic groups). Hence,
![]() $K_0(A^\alpha )$
and
$K_0(A^\alpha )$
and
![]() $K_1(A^\alpha )$
are both finitely generated, being a quotient and a subgroup of
$K_1(A^\alpha )$
are both finitely generated, being a quotient and a subgroup of
![]() $K_1(A)$
, respectively. The argument given in the proof of part (2) above shows that there is an isomorphism
$K_1(A)$
, respectively. The argument given in the proof of part (2) above shows that there is an isomorphism
![]() $K_0(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
. Thus
$K_0(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
. Thus
![]() $K_0(A)$
is also finitely generated, and repeating the same argument again, exchanging the roles of
$K_0(A)$
is also finitely generated, and repeating the same argument again, exchanging the roles of
![]() $K_0$
and
$K_0$
and
![]() $K_1$
, shows that
$K_1$
, shows that
![]() $K_1(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
.
$K_1(A)\cong K_0(A^\alpha )\oplus K_1(A^\alpha )$
.
In reference to part (2) of Theorem 3.3, we mention that it is not in general true that a pure subgroup of a direct sum of cyclic groups is automatically a direct summand. For example, set
![]() $G=\bigoplus _{n\in {\mathbb {N}}} {\mathbb {Z}}_{2^n}$
, with canonical generators
$G=\bigoplus _{n\in {\mathbb {N}}} {\mathbb {Z}}_{2^n}$
, with canonical generators
![]() $x_n\in {\mathbb {Z}}_{2^n}$
for
$x_n\in {\mathbb {Z}}_{2^n}$
for
![]() $n\in {\mathbb {N}}$
, and let H be the subgroup generated by
$n\in {\mathbb {N}}$
, and let H be the subgroup generated by
![]() $\{x_n-2x_{n+1}\colon n\in {\mathbb {N}}\}$
. Then H is pure in G but not a direct summand.
$\{x_n-2x_{n+1}\colon n\in {\mathbb {N}}\}$
. Then H is pure in G but not a direct summand.
4 Circle actions on Kirchberg algebras
This section contains our main results concerning
![]() $KK^{\mathbb {T}}$
-theory for Rokhlin actions. This includes Theorems C and F from the introduction. In the presence of the UCT, any isomorphism between the pure extensions from Theorem 3.3 lifts to a
$KK^{\mathbb {T}}$
-theory for Rokhlin actions. This includes Theorems C and F from the introduction. In the presence of the UCT, any isomorphism between the pure extensions from Theorem 3.3 lifts to a
![]() $KK^{\mathbb {T}}$
-equivalence. We show by means of an example that an isomorphism of the K- and
$KK^{\mathbb {T}}$
-equivalence. We show by means of an example that an isomorphism of the K- and
![]() $K^{\mathbb {T}}$
-theories does not necessarily lift to a
$K^{\mathbb {T}}$
-theories does not necessarily lift to a
![]() $KK^{\mathbb {T}}$
-equivalence (see Example 4.7). Finally, we also describe the extensions that arise as
$KK^{\mathbb {T}}$
-equivalence (see Example 4.7). Finally, we also describe the extensions that arise as
![]() ${\mathrm {Ext}}_\ast (\alpha )$
for a Rokhlin action
${\mathrm {Ext}}_\ast (\alpha )$
for a Rokhlin action
![]() $\alpha $
on a Kirchberg algebra satisfying the UCT (see Theorem 4.8).
$\alpha $
on a Kirchberg algebra satisfying the UCT (see Theorem 4.8).
Definition 4.1 Let A be a simple unital
![]() $C^*$
-algebra. Then A is said to be:
$C^*$
-algebra. Then A is said to be:
-
(1) purely infinite, if for every
 $a\in A\setminus \{0\}$
there are
$a\in A\setminus \{0\}$
there are
 $x,y\in A$
with
$x,y\in A$
with
 $xay=1$
,
$xay=1$
, -
(2) a Kirchberg algebra, if it is purely infinite, separable and nuclear.
Recall that an automorphism
![]() $\varphi $
of a
$\varphi $
of a
![]() $C^*$
-algebra is said to be aperiodic if
$C^*$
-algebra is said to be aperiodic if
![]() $\varphi ^n$
is not inner for all
$\varphi ^n$
is not inner for all
![]() $n\geq 1$
.
$n\geq 1$
.
Proposition 4.2 Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property.
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property.
-
(1) A is simple if and only if
 $A^\alpha $
is simple and
$A^\alpha $
is simple and
 $\check {\alpha }$
is aperiodic.
$\check {\alpha }$
is aperiodic. -
(2) A is purely infinite simple if and only if
 $A^\alpha $
is purely infinite simple and
$A^\alpha $
is purely infinite simple and
 $\check {\alpha }$
is aperiodic.
$\check {\alpha }$
is aperiodic. -
(3) A is a Kirchberg algebra if and only if
 $A^\alpha $
is a Kirchberg algebra and
$A^\alpha $
is a Kirchberg algebra and
 $\check {\alpha }$
is aperiodic.
$\check {\alpha }$
is aperiodic. -
(4) A satisfies the UCT if and only if
 $A^\alpha $
satisfies the UCT.
$A^\alpha $
satisfies the UCT.
Proof (1). If A is simple, then
![]() $A^\alpha $
is simple by Corollary 2.5. We show that
$A^\alpha $
is simple by Corollary 2.5. We show that
![]() $\check {\alpha }$
is aperiodic. Arguing by contradiction, suppose that there exist
$\check {\alpha }$
is aperiodic. Arguing by contradiction, suppose that there exist
![]() $n\geq 1$
and a unitary
$n\geq 1$
and a unitary
![]() $v\in A^\alpha $
such that
$v\in A^\alpha $
such that
![]() $\check {\alpha }^n={\mathrm {Ad}}(v)$
. Set
$\check {\alpha }^n={\mathrm {Ad}}(v)$
. Set
Then
![]() $\check {\alpha }^{n^2}={\mathrm {Ad}}(w)$
. Using that
$\check {\alpha }^{n^2}={\mathrm {Ad}}(w)$
. Using that
![]() $\check {\alpha }^n(v)=v$
at the second step, that
$\check {\alpha }^n(v)=v$
at the second step, that
![]() $vx=\check {\alpha }^n(x)v$
for all
$vx=\check {\alpha }^n(x)v$
for all
![]() $x\in A^\alpha $
at the third, and that
$x\in A^\alpha $
at the third, and that
![]() $\check {\alpha }^{-n}(v)=v$
at he fifth, we get
$\check {\alpha }^{-n}(v)=v$
at he fifth, we get
 $$ \begin{align*} \check{\alpha}(w)&= \check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) \check{\alpha}^{n}(v)= \check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) v\\ &=v\check{\alpha}^{-n}\big(\check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) \big)= v\check{\alpha}\big(\check{\alpha}^{-n}(v)\big)\check{\alpha}^2\big(\check{\alpha}^{-n}(v)\big)\dots\check{\alpha}^{n-1}(\check{\alpha}^{-n}(v)\big)\\ &=v\check{\alpha}(v)\dots\check{\alpha}^{n-1}(v)=w. \end{align*} $$
$$ \begin{align*} \check{\alpha}(w)&= \check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) \check{\alpha}^{n}(v)= \check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) v\\ &=v\check{\alpha}^{-n}\big(\check{\alpha}(v)\check{\alpha}^2(v)\dots\check{\alpha}^{n-1}(v) \big)= v\check{\alpha}\big(\check{\alpha}^{-n}(v)\big)\check{\alpha}^2\big(\check{\alpha}^{-n}(v)\big)\dots\check{\alpha}^{n-1}(\check{\alpha}^{-n}(v)\big)\\ &=v\check{\alpha}(v)\dots\check{\alpha}^{n-1}(v)=w. \end{align*} $$
It follows that w is
![]() $\check {\alpha }$
-invariant. With u denoting the canonical unitary in
$\check {\alpha }$
-invariant. With u denoting the canonical unitary in
![]() $A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
that implements
$A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
that implements
![]() $\check {\alpha }$
, we therefore have
$\check {\alpha }$
, we therefore have
![]() $uwu^*=w$
. Set
$uwu^*=w$
. Set
![]() $z=u^{n^2}w^*$
. It is clear that z commutes with u, and for
$z=u^{n^2}w^*$
. It is clear that z commutes with u, and for
![]() $a\in A^\alpha $
we have
$a\in A^\alpha $
we have
so z belongs to the center of
![]() $A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}\cong A$
. Since A is simple, its center is trivial and thus there is
$A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}\cong A$
. Since A is simple, its center is trivial and thus there is
![]() $\lambda \in {\mathbb {C}}$
with
$\lambda \in {\mathbb {C}}$
with
![]() $u^{n^2}=\lambda w$
. In particular,
$u^{n^2}=\lambda w$
. In particular,
![]() $u^{n^2}$
belongs to
$u^{n^2}$
belongs to
![]() $A^\alpha $
, which is a contradiction. This shows that
$A^\alpha $
, which is a contradiction. This shows that
![]() $\check {\alpha }$
is aperiodic.
$\check {\alpha }$
is aperiodic.
Conversely, if
![]() $\check {\alpha }$
is aperiodic and
$\check {\alpha }$
is aperiodic and
![]() $A^\alpha $
is simple, it follows from Theorem 3.1 in [Reference Kishimoto21] that the crossed product
$A^\alpha $
is simple, it follows from Theorem 3.1 in [Reference Kishimoto21] that the crossed product
![]() $A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}\cong A$
is simple.
$A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}\cong A$
is simple.
(2). Assume that A is purely infinite simple. Then
![]() $\check {\alpha }$
is aperiodic by part (1). Let
$\check {\alpha }$
is aperiodic by part (1). Let
![]() $a\in A^\alpha $
be nonzero, and let
$a\in A^\alpha $
be nonzero, and let
![]() $\varepsilon>0$
small enough so that
$\varepsilon>0$
small enough so that
![]() $\varepsilon ^3+3\varepsilon <1$
. Without loss of generality, we assume that
$\varepsilon ^3+3\varepsilon <1$
. Without loss of generality, we assume that
![]() $\|a\|=1$
. Find
$\|a\|=1$
. Find
![]() $x,y\in A$
such that
$x,y\in A$
such that
![]() $xay=1$
. By Lemma 4.1.7 in [Reference Rørdam and Størmer37], we may assume that
$xay=1$
. By Lemma 4.1.7 in [Reference Rørdam and Størmer37], we may assume that
![]() $\|x\|<1+\varepsilon $
and
$\|x\|<1+\varepsilon $
and
![]() $\|y\|<1+\varepsilon $
. Let
$\|y\|<1+\varepsilon $
. Let
![]() $\sigma \colon A\to A^\alpha $
a completely positive unital map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
$\sigma \colon A\to A^\alpha $
a completely positive unital map as in the conclusion of Theorem 2.11 in [Reference Gardella12] for
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $F_2=\{x,y,xa,a\}$
and
$F_2=\{x,y,xa,a\}$
and
![]() $F_1=\{a\}$
. Then
$F_1=\{a\}$
. Then
Hence
![]() $\|\sigma (x)a\sigma (y)-1\|\leq \varepsilon ^3+3\varepsilon <1$
. It follows that
$\|\sigma (x)a\sigma (y)-1\|\leq \varepsilon ^3+3\varepsilon <1$
. It follows that
![]() $\sigma (x)a\sigma (y)$
is invertible. With
$\sigma (x)a\sigma (y)$
is invertible. With
![]() $z\in A^\alpha $
denoting its inverse, we have
$z\in A^\alpha $
denoting its inverse, we have
![]() $\sigma (x)a\sigma (y)z=1$
, as desired.
$\sigma (x)a\sigma (y)z=1$
, as desired.
Conversely, assume that
![]() $\check {\alpha }$
is aperiodic and
$\check {\alpha }$
is aperiodic and
![]() $A^\alpha $
is purely infinite simple. Then
$A^\alpha $
is purely infinite simple. Then
![]() $A\cong A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
is purely infinite simple by Corollary 4.6 in [Reference Jeong and Osaka18].
$A\cong A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}}$
is purely infinite simple by Corollary 4.6 in [Reference Jeong and Osaka18].
(3). This follows from (1) and (2), since A is nuclear (respectively, separable) if and only if so is
![]() $A^\alpha $
.
$A^\alpha $
.
(4). If A satisfies the UCT, then so does
![]() $A^\alpha $
by Theorem 3.13 in [Reference Gardella10]. The converse follows from the fact that the UCT is preserved by
$A^\alpha $
by Theorem 3.13 in [Reference Gardella10]. The converse follows from the fact that the UCT is preserved by
![]() ${\mathbb {Z}}$
-crossed products.
${\mathbb {Z}}$
-crossed products.
Remark 4.3 Let the notation be as in Proposition 4.2.
-
• Simplicity of A is really needed in (1) to conclude that
 $\check {\alpha }$
is aperiodic, even if
$\check {\alpha }$
is aperiodic, even if
 $A^\alpha $
is simple. Consider for example the trivial automorphism of
$A^\alpha $
is simple. Consider for example the trivial automorphism of
 ${\mathbb {C}}$
, whose dual action is the left translation action
${\mathbb {C}}$
, whose dual action is the left translation action
 $\texttt {Lt}\colon {\mathbb {T}}\to {\mathrm {Aut}}(C({\mathbb {T}}))$
.
$\texttt {Lt}\colon {\mathbb {T}}\to {\mathrm {Aut}}(C({\mathbb {T}}))$
. -
• Outerness of
 $\alpha $
is not enough in (2) to deduce pure infiniteness of
$\alpha $
is not enough in (2) to deduce pure infiniteness of
 $A^\alpha $
from pure infiniteness of A (unlike for finite groups). For example, the fixed point algebra of
$A^\alpha $
from pure infiniteness of A (unlike for finite groups). For example, the fixed point algebra of
 ${\mathcal {O}_{\infty }}$
by its gauge action is AF (and not even simple).
${\mathcal {O}_{\infty }}$
by its gauge action is AF (and not even simple).
We will need some terminology.
Definition 4.4 Let G be a second countable, locally compact group (in this work either
![]() ${\mathbb {T}}$
,
${\mathbb {T}}$
,
![]() ${\mathbb {Z}}$
, or the trivial group), let A and B be separable, unital
${\mathbb {Z}}$
, or the trivial group), let A and B be separable, unital
![]() $C^*$
-algebras, and let
$C^*$
-algebras, and let
![]() $\alpha \colon G\to {\mathrm {Aut}}(A)$
and
$\alpha \colon G\to {\mathrm {Aut}}(A)$
and
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
be actions. We say that
$\beta \colon G\to {\mathrm {Aut}}(B)$
be actions. We say that
![]() $(A,\alpha )$
and
$(A,\alpha )$
and
![]() $(B,\beta )$
are unitally
$(B,\beta )$
are unitally
![]() $KK^G$
-equivalent, if there is an invertible class
$KK^G$
-equivalent, if there is an invertible class
![]() $\eta \in KK^G(A,B)$
with
$\eta \in KK^G(A,B)$
with
![]() $[1_A]\times \eta =[1_B]$
. In this situation, we say that
$[1_A]\times \eta =[1_B]$
. In this situation, we say that
![]() $\eta $
is a unital
$\eta $
is a unital
![]() $KK^G$
-equivalence.
$KK^G$
-equivalence.
A unital
![]() $KK^{\mathbb {Z}}$
-equivalence between two
$KK^{\mathbb {Z}}$
-equivalence between two
![]() ${\mathbb {Z}}$
-actions
${\mathbb {Z}}$
-actions
![]() $(A,\sigma )$
and
$(A,\sigma )$
and
![]() $(B,\theta )$
naturally induces an isomorphism between the Pimsner–Voiculescu 6-term exact sequences of
$(B,\theta )$
naturally induces an isomorphism between the Pimsner–Voiculescu 6-term exact sequences of
![]() $\sigma $
and
$\sigma $
and
![]() $\theta $
which moreover preserves the classes of the units; this can be found in [Reference Meyer and Nest29], and a special case will be proved in Theorem 4.6. If the automorphisms are moreover approximately inner, then each of these 6-term exact sequences splits into two short exact sequences. The resulting equivalence relation for sums of short exact sequences (with distinguished classes) is the following:
$\theta $
which moreover preserves the classes of the units; this can be found in [Reference Meyer and Nest29], and a special case will be proved in Theorem 4.6. If the automorphisms are moreover approximately inner, then each of these 6-term exact sequences splits into two short exact sequences. The resulting equivalence relation for sums of short exact sequences (with distinguished classes) is the following:
Definition 4.5 For
![]() $j=0,1$
, let
$j=0,1$
, let
![]() $K^{\mathcal {E}}_j, G^{\mathcal {E}}_j, K^{\mathcal {F}}_j$
, and
$K^{\mathcal {E}}_j, G^{\mathcal {E}}_j, K^{\mathcal {F}}_j$
, and
![]() $G^{\mathcal {F}}_j$
be countable abelian groups, let
$G^{\mathcal {F}}_j$
be countable abelian groups, let
![]() $k^{\mathcal {E}}_0\in K^{\mathcal {E}}_0$
and
$k^{\mathcal {E}}_0\in K^{\mathcal {E}}_0$
and
![]() $k^{\mathcal {F}}_0\in K^{\mathcal {F}}_0$
, and let
$k^{\mathcal {F}}_0\in K^{\mathcal {F}}_0$
, and let
be short exact sequences. We say that
![]() $(\mathcal {E}_0,\mathcal {E}_1,k_0^{\mathcal {E}})$
is isomorphic to
$(\mathcal {E}_0,\mathcal {E}_1,k_0^{\mathcal {E}})$
is isomorphic to
![]() $(\mathcal {F}_0,\mathcal {F}_1,k_0^{\mathcal {F}})$
if there exist group isomorphisms
$(\mathcal {F}_0,\mathcal {F}_1,k_0^{\mathcal {F}})$
if there exist group isomorphisms
![]() $\varphi _j \colon K_j^{\mathcal {E}}\to K_j^{\mathcal {F}}$
and
$\varphi _j \colon K_j^{\mathcal {E}}\to K_j^{\mathcal {F}}$
and
![]() $\psi _j \colon G_j^{\mathcal {E}}\to G_j^{\mathcal {F}}$
with
$\psi _j \colon G_j^{\mathcal {E}}\to G_j^{\mathcal {F}}$
with
![]() $\varphi _0(k_0^{\mathcal {E}})=k_0^{\mathcal {F}}$
making the following diagram commute:
$\varphi _0(k_0^{\mathcal {E}})=k_0^{\mathcal {F}}$
making the following diagram commute:

This is different from having two isomorphisms
![]() $(\mathcal {E}_0,k_0^{\mathcal {E}})\cong (\mathcal {F}_0,k_0^{\mathcal {F}})$
and
$(\mathcal {E}_0,k_0^{\mathcal {E}})\cong (\mathcal {F}_0,k_0^{\mathcal {F}})$
and
![]() $\mathcal {E}_1\cong \mathcal {F}_1$
, since, for example, we require the isomorphism
$\mathcal {E}_1\cong \mathcal {F}_1$
, since, for example, we require the isomorphism
![]() $K_0^{\mathcal {E}}\cong K_0^{\mathcal {F}}$
to be the same both in the isomorphism
$K_0^{\mathcal {E}}\cong K_0^{\mathcal {F}}$
to be the same both in the isomorphism
![]() $\mathcal {E}_0\cong \mathcal {F}_0$
and in
$\mathcal {E}_0\cong \mathcal {F}_0$
and in
![]() $\mathcal {E}_1\cong \mathcal {F}_1$
.
$\mathcal {E}_1\cong \mathcal {F}_1$
.
We are now ready to prove that Rokhlin actions of the circle on unital Kirchberg algebras are conjugate if they are unitally
![]() $KK^{\mathbb {T}}$
-equivalent.
$KK^{\mathbb {T}}$
-equivalent.
Theorem 4.6 Let A and B be unital Kirchberg algebras, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
and
![]() $\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
be actions with the Rokhlin property. Then
$\beta \colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
be actions with the Rokhlin property. Then
![]() $(A,\alpha )$
and
$(A,\alpha )$
and
![]() $(B,\beta )$
are conjugate if and only if they are unitally
$(B,\beta )$
are conjugate if and only if they are unitally
![]() $KK^{\mathbb {T}}$
-equivalent.
$KK^{\mathbb {T}}$
-equivalent.
When A and B satisfy the UCT, these conditions are equivalent to the existence of an isomorphism
![]() $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
in the sense of Definition 4.5.
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
in the sense of Definition 4.5.
Proof Assume that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are unitally
$\beta $
are unitally
![]() $KK^{\mathbb {T}}$
-equivalent, and fix a unital
$KK^{\mathbb {T}}$
-equivalent, and fix a unital
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $\xi \in KK^{\mathbb {T}}\big ((A,\alpha ),(B,\beta )\big )$
. Denote by
$\xi \in KK^{\mathbb {T}}\big ((A,\alpha ),(B,\beta )\big )$
. Denote by
![]() $\xi \rtimes {\mathbb {T}}$
the
$\xi \rtimes {\mathbb {T}}$
the
![]() $KK^{\mathbb {Z}}$
-equivalence between
$KK^{\mathbb {Z}}$
-equivalence between
![]() $(A\rtimes _\alpha {\mathbb {T}},\widehat {\alpha })$
and
$(A\rtimes _\alpha {\mathbb {T}},\widehat {\alpha })$
and
![]() $(B\rtimes _\beta {\mathbb {T}},\widehat {\beta })$
that
$(B\rtimes _\beta {\mathbb {T}},\widehat {\beta })$
that
![]() $\xi $
induces. Combining Takai duality with Theorem 2.3, it follows that
$\xi $
induces. Combining Takai duality with Theorem 2.3, it follows that
![]() $\xi \rtimes {\mathbb {T}}$
induces a
$\xi \rtimes {\mathbb {T}}$
induces a
![]() $KK^{\mathbb {Z}}$
-equivalence
$KK^{\mathbb {Z}}$
-equivalence
![]() $\eta $
between
$\eta $
between
![]() $(A^\alpha ,\check {\alpha })$
and
$(A^\alpha ,\check {\alpha })$
and
![]() $(B^\beta ,\check {\beta })$
. Since
$(B^\beta ,\check {\beta })$
. Since
![]() $\xi $
is unital, we can choose
$\xi $
is unital, we can choose
![]() $\eta $
to be unital as well.
$\eta $
to be unital as well.
Since
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $B^\beta $
are Kirchberg algebras by part (3) of Proposition 4.2, it follows from Theorem 4.2.1 in [Reference Phillips35] that there exists an isomorphism
$B^\beta $
are Kirchberg algebras by part (3) of Proposition 4.2, it follows from Theorem 4.2.1 in [Reference Phillips35] that there exists an isomorphism
![]() $\phi \colon A^\alpha \to B^\beta $
such that
$\phi \colon A^\alpha \to B^\beta $
such that
![]() $KK(\phi )=\eta $
. Since
$KK(\phi )=\eta $
. Since
![]() $\eta $
is equivariant, it follows that
$\eta $
is equivariant, it follows that
![]() $\phi \circ \check {\alpha }\circ \phi ^{-1}$
and
$\phi \circ \check {\alpha }\circ \phi ^{-1}$
and
![]() $\check {\beta }$
determine the same class in
$\check {\beta }$
determine the same class in
![]() $KK(B^\beta ,B^\beta )$
. Since A and B are simple, it follows from part (1) of Proposition 4.2 that
$KK(B^\beta ,B^\beta )$
. Since A and B are simple, it follows from part (1) of Proposition 4.2 that
![]() $\check {\alpha }$
and
$\check {\alpha }$
and
![]() $\check {\beta }$
are aperiodic. Thus, by the equivalence between (1’) and (3’) in Theorem 9 in [Reference Nakamura30],
$\check {\beta }$
are aperiodic. Thus, by the equivalence between (1’) and (3’) in Theorem 9 in [Reference Nakamura30],
![]() $\phi \circ \check {\alpha }\circ \phi ^{-1}$
and
$\phi \circ \check {\alpha }\circ \phi ^{-1}$
and
![]() $\check {\beta }$
, and thus
$\check {\beta }$
, and thus
![]() $\check {\alpha }$
and
$\check {\alpha }$
and
![]() $\check {\beta }$
, are cocycle conjugateFootnote
2
. It follows that their dual actions are conjugate, and hence
$\check {\beta }$
, are cocycle conjugateFootnote
2
. It follows that their dual actions are conjugate, and hence
![]() $(A,\alpha )\cong (B,\beta )$
as desired.
$(A,\alpha )\cong (B,\beta )$
as desired.
We turn to the last part of the statement. Fix a unital
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $\rho \in KK^{\mathbb {T}}((A,\alpha ),(B,\beta ))$
. Arguing as in the first part using Baaj–Skandalis duality, we obtain a unital
$\rho \in KK^{\mathbb {T}}((A,\alpha ),(B,\beta ))$
. Arguing as in the first part using Baaj–Skandalis duality, we obtain a unital
![]() $KK^{\mathbb {Z}}$
-equivalence
$KK^{\mathbb {Z}}$
-equivalence
Denote by
![]() $\mathcal {F}(\eta )\in KK(A^\alpha ,B^\beta )$
the
$\mathcal {F}(\eta )\in KK(A^\alpha ,B^\beta )$
the
![]() $KK$
-equivalence that
$KK$
-equivalence that
![]() $\eta $
induces under the forgetful functor
$\eta $
induces under the forgetful functor
![]() $KK^{\mathbb {Z}}\to KK$
. Similarly, we let
$KK^{\mathbb {Z}}\to KK$
. Similarly, we let
![]() $\mathcal {F}(\eta \rtimes {\mathbb {Z}})\in KK(A,A)$
denote the
$\mathcal {F}(\eta \rtimes {\mathbb {Z}})\in KK(A,A)$
denote the
![]() $KK$
-equivalence that
$KK$
-equivalence that
![]() $\eta \rtimes {\mathbb {Z}}$
induces, which can be canonically identified with
$\eta \rtimes {\mathbb {Z}}$
induces, which can be canonically identified with
![]() $\mathcal {F}(\rho )$
. Using naturality of the functors involved, we deduce that the diagram
$\mathcal {F}(\rho )$
. Using naturality of the functors involved, we deduce that the diagram

commutes. Since all vertical maps are isomorphisms and
![]() $\mathcal {F}(\eta )_0([1_{A^\alpha }])=[1_{B^\beta }]$
, we deduce that
$\mathcal {F}(\eta )_0([1_{A^\alpha }])=[1_{B^\beta }]$
, we deduce that
![]() $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
.
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
.
We now prove the converse, so assume that A and B satisfy the UCT. By part (4) of Proposition 4.2,
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $B^\beta $
also satisfy the UCT. Since
$B^\beta $
also satisfy the UCT. Since
![]() $\check {\alpha }$
and
$\check {\alpha }$
and
![]() $\check {\beta }$
are approximately inner, an isomorphism
$\check {\beta }$
are approximately inner, an isomorphism
![]() $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
is equivalent to
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong ({\mathrm {Ext}}_\ast (\beta ),[1_{B^\beta }])$
is equivalent to
![]() $\check {\alpha }$
and
$\check {\alpha }$
and
![]() $\check {\beta }$
having isomorphic Pimsner–Voiculescu 6-term exact sequences (in a unit-preserving way); see the comments before Definition 4.5. It thus follows from Theorem 2.12 in [Reference Meyer28] that
$\check {\beta }$
having isomorphic Pimsner–Voiculescu 6-term exact sequences (in a unit-preserving way); see the comments before Definition 4.5. It thus follows from Theorem 2.12 in [Reference Meyer28] that
![]() $(A^\alpha ,\check {\alpha })$
is unitally
$(A^\alpha ,\check {\alpha })$
is unitally
![]() $KK^{\mathbb {Z}}$
-equivalent to
$KK^{\mathbb {Z}}$
-equivalent to
![]() $(B^\beta ,\check {\beta })$
. Again by Baaj–Skandalis duality, it follows that
$(B^\beta ,\check {\beta })$
. Again by Baaj–Skandalis duality, it follows that
![]() $(A,\alpha )$
is unitally
$(A,\alpha )$
is unitally
![]() $KK^{\mathbb {T}}$
-equivalent to
$KK^{\mathbb {T}}$
-equivalent to
![]() $(B,\beta )$
. This finishes the proof.
$(B,\beta )$
. This finishes the proof.
In the context of Theorem 4.6, the assumption that the diagram (4.1) from Definition 4.5 commutes cannot be dropped, and it is not enough to have isomorphisms
![]() $K_\ast (A^\alpha )\cong K_\ast (B^\beta )$
and
$K_\ast (A^\alpha )\cong K_\ast (B^\beta )$
and
![]() $K_\ast (A)\cong K_\ast (B)$
. In the next example, we construct a Kirchberg algebra A satisfying the UCT, and two actions
$K_\ast (A)\cong K_\ast (B)$
. In the next example, we construct a Kirchberg algebra A satisfying the UCT, and two actions
![]() $\alpha ,\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
with the Rokhlin property, such that
$\alpha ,\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
with the Rokhlin property, such that
![]() $A^\alpha \cong A^\gamma $
but
$A^\alpha \cong A^\gamma $
but
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are not conjugate. In particular, the example shows that an isomorphism of the
$\gamma $
are not conjugate. In particular, the example shows that an isomorphism of the
![]() $K^{\mathbb {T}}$
-theory cannot in general be lifted to a
$K^{\mathbb {T}}$
-theory cannot in general be lifted to a
![]() $KK^{\mathbb {T}}$
-equivalence.
$KK^{\mathbb {T}}$
-equivalence.
In preparation for our construction, we introduce some notation. If B is a unital
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $\varphi \in {\mathrm {Aut}}(B)$
is an approximately inner automorphism, then the Pimsner–Voiculescu exact sequence for
$\varphi \in {\mathrm {Aut}}(B)$
is an approximately inner automorphism, then the Pimsner–Voiculescu exact sequence for
![]() $\varphi $
reduces to the short exact sequences
$\varphi $
reduces to the short exact sequences
for
![]() $j=0,1$
. We denote by
$j=0,1$
. We denote by
![]() $\eta _j(\varphi ) \in {\mathrm {Ext}}(K_{1-j}(B),K_j(B))$
the class of the above extension. Note that if
$\eta _j(\varphi ) \in {\mathrm {Ext}}(K_{1-j}(B),K_j(B))$
the class of the above extension. Note that if
![]() $\varphi ,\psi \in {\mathrm {Aut}}(B)$
are cocycle conjugate automorphisms, then
$\varphi ,\psi \in {\mathrm {Aut}}(B)$
are cocycle conjugate automorphisms, then
![]() $\eta _j(\varphi )=\eta _j(\psi )$
.
$\eta _j(\varphi )=\eta _j(\psi )$
.
Example 4.7 Let p be a prime number. Let
![]() $\xi _0\in \mathrm {Ext}_{\mathbb {Z}}^1\big ({\mathbb {Z}}\big [\tfrac {1}{p}\big ],{\mathbb {Z}} \big )$
be a nontrivial class, and fix a representing extension
$\xi _0\in \mathrm {Ext}_{\mathbb {Z}}^1\big ({\mathbb {Z}}\big [\tfrac {1}{p}\big ],{\mathbb {Z}} \big )$
be a nontrivial class, and fix a representing extension
Set
Then K and E are torsion free and abelian. Using that
![]() $E_0$
is a nontrivial extension of
$E_0$
is a nontrivial extension of
![]() ${\mathbb {Z}}\big [\tfrac {1}{p}\big ]$
by
${\mathbb {Z}}\big [\tfrac {1}{p}\big ]$
by
![]() ${\mathbb {Z}}$
, fix a nontrivial extension
${\mathbb {Z}}$
, fix a nontrivial extension
and write
![]() $\xi \in {\mathrm {Ext}}(K,K)$
for the induced class. Since K is torsion free, it follows that the extension in (4.3) is pure. Note that there is also an isomorphism
$\xi \in {\mathrm {Ext}}(K,K)$
for the induced class. Since K is torsion free, it follows that the extension in (4.3) is pure. Note that there is also an isomorphism
![]() $E\cong K\oplus K$
. (In other words, and this is a crucial ingredient in the construction, the group E can be written in two nonequivalent ways as an extension of K by itself.)
$E\cong K\oplus K$
. (In other words, and this is a crucial ingredient in the construction, the group E can be written in two nonequivalent ways as an extension of K by itself.)
Set
![]() $k_0=(1_{{\mathbb {Q}}},0,0,\ldots )\in K$
and
$k_0=(1_{{\mathbb {Q}}},0,0,\ldots )\in K$
and
![]() $e_0=(k_0,k_0)\in E$
. Since K is torsion-free, we may use Elliott’s classification of simple A
$e_0=(k_0,k_0)\in E$
. Since K is torsion-free, we may use Elliott’s classification of simple A
![]() ${\mathbb {T}}$
-algebras with real rank zero (see the comments before Proposition 3.2.7 in [Reference Rørdam and Størmer37]), to find a simple, unital A
${\mathbb {T}}$
-algebras with real rank zero (see the comments before Proposition 3.2.7 in [Reference Rørdam and Størmer37]), to find a simple, unital A
![]() ${\mathbb {T}}$
-algebra C satisfying
${\mathbb {T}}$
-algebra C satisfying
![]() $K_0(C)\cong K_1(C)\cong K$
with
$K_0(C)\cong K_1(C)\cong K$
with
![]() $[1_C]$
corresponding to
$[1_C]$
corresponding to
![]() $k_0\in K$
. Use the case
$k_0\in K$
. Use the case
![]() $i=1$
of Theorem 3.1 in [Reference Kishimoto and Kumjian24] to find an approximately inner automorphism
$i=1$
of Theorem 3.1 in [Reference Kishimoto and Kumjian24] to find an approximately inner automorphism
![]() $\varphi \in {\mathrm {Aut}}(C)$
with
$\varphi \in {\mathrm {Aut}}(C)$
with
![]() $\eta _0(\varphi )=0$
and
$\eta _0(\varphi )=0$
and
![]() $\eta _1(\varphi )=\xi \in {\mathrm {Ext}}(K,K)$
. Then
$\eta _1(\varphi )=\xi \in {\mathrm {Ext}}(K,K)$
. Then
The proof of Theorem 3.1 in [Reference Kishimoto and Kumjian24] is in fact constructive, and the argument used to prove the case
![]() $i=1$
shows that
$i=1$
shows that
![]() $\varphi $
can be chosen to be approximately representable. Indeed, it is shown in Section 3.11 of [Reference Kishimoto and Kumjian24] that there is an increasing sequence
$\varphi $
can be chosen to be approximately representable. Indeed, it is shown in Section 3.11 of [Reference Kishimoto and Kumjian24] that there is an increasing sequence
![]() $(C_n)_{n\in {\mathbb {N}}}$
of unital subalgebras of C with
$(C_n)_{n\in {\mathbb {N}}}$
of unital subalgebras of C with
![]() $C=\varinjlim C_n$
, and unitaries
$C=\varinjlim C_n$
, and unitaries
![]() $u_n\in C_n$
satisfying
$u_n\in C_n$
satisfying
![]() $\varphi =\varinjlim {\mathrm {Ad}}(u_n)$
.
$\varphi =\varinjlim {\mathrm {Ad}}(u_n)$
.
Claim:
![]() $\varphi $
is aperiodic. Arguing by contradiction, suppose that there exist
$\varphi $
is aperiodic. Arguing by contradiction, suppose that there exist
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $u\in {\mathcal {U}}(C)$
such that
$u\in {\mathcal {U}}(C)$
such that
![]() $\varphi ^n={\mathrm {Ad}}(u)$
. Set
$\varphi ^n={\mathrm {Ad}}(u)$
. Set
![]() $v=u\varphi (u)\dots \varphi ^{n-1}(u)\in C$
. Then
$v=u\varphi (u)\dots \varphi ^{n-1}(u)\in C$
. Then
![]() $\varphi ^{n^2}={\mathrm {Ad}}(v)$
and v is
$\varphi ^{n^2}={\mathrm {Ad}}(v)$
and v is
![]() $\varphi ^{n^2}$
-invariant. Moreover, we have
$\varphi ^{n^2}$
-invariant. Moreover, we have
 $$ \begin{align*} \varphi(v)&= \varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) \varphi^{n}(u)= \varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) u\\ &=u\varphi^{-n}\big(\varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) \big)= u\varphi\big(\varphi^{-n}(u)\big)\varphi^2\big(\varphi^{-n}(u)\big)\dots\varphi^{n-1}(\varphi^{-n}(u)\big)\\ &=u\varphi(u)\dots\varphi^{n-1}(u)=v, \end{align*} $$
$$ \begin{align*} \varphi(v)&= \varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) \varphi^{n}(u)= \varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) u\\ &=u\varphi^{-n}\big(\varphi(u)\varphi^2(u)\dots\varphi^{n-1}(u) \big)= u\varphi\big(\varphi^{-n}(u)\big)\varphi^2\big(\varphi^{-n}(u)\big)\dots\varphi^{n-1}(\varphi^{-n}(u)\big)\\ &=u\varphi(u)\dots\varphi^{n-1}(u)=v, \end{align*} $$
and thus v is
![]() $\varphi $
-invariant. Denote by D the twisted crossed product of C by
$\varphi $
-invariant. Denote by D the twisted crossed product of C by
![]() $\varphi $
with respect to the twist induced by v. By Theorem 2.4 in [Reference Olesen and Pedersen32], the crossed product
$\varphi $
with respect to the twist induced by v. By Theorem 2.4 in [Reference Olesen and Pedersen32], the crossed product
![]() $C\rtimes _\varphi {\mathbb {Z}}$
is isomorphic to the induced algebra
$C\rtimes _\varphi {\mathbb {Z}}$
is isomorphic to the induced algebra
![]() $\mathrm {Ind}_{(n^2{\mathbb {Z}})^{\perp }}^{\mathbb {T}} (D)$
. By compactness of
$\mathrm {Ind}_{(n^2{\mathbb {Z}})^{\perp }}^{\mathbb {T}} (D)$
. By compactness of
![]() ${\mathbb {T}}$
, this induced algebra is isomorphic to
${\mathbb {T}}$
, this induced algebra is isomorphic to
![]() $C({\mathbb {T}},D)$
. In particular,
$C({\mathbb {T}},D)$
. In particular,
We proceed to compute the K-theory of D. Set
![]() ${\mathcal {K}}={\mathcal {K}}(\ell ^2({\mathbb {Z}}))$
. By Theorem 3.4 in [Reference Packer and Raeburn33], there is an automorphism
${\mathcal {K}}={\mathcal {K}}(\ell ^2({\mathbb {Z}}))$
. By Theorem 3.4 in [Reference Packer and Raeburn33], there is an automorphism
![]() $\varphi _0$
of
$\varphi _0$
of
![]() $C\otimes {\mathcal {K}}$
whose crossed product is isomorphic to D (this is the so-called Packer–Raeburn stabilization trick). An explicit formula for
$C\otimes {\mathcal {K}}$
whose crossed product is isomorphic to D (this is the so-called Packer–Raeburn stabilization trick). An explicit formula for
![]() $\varphi _0$
is given at the beginning of the proof on page 301 (see Equation (3.1)), which shows that we can choose
$\varphi _0$
is given at the beginning of the proof on page 301 (see Equation (3.1)), which shows that we can choose
![]() $\varphi _0$
to be unitarily equivalent to
$\varphi _0$
to be unitarily equivalent to
![]() $\varphi \otimes {\mathrm {id}}_{{\mathcal {K}}}$
(see also the top line on page 302). It follows that D is isomorphic to
$\varphi \otimes {\mathrm {id}}_{{\mathcal {K}}}$
(see also the top line on page 302). It follows that D is isomorphic to
![]() $(C\otimes {\mathcal {K}})\rtimes _{\varphi \otimes {\mathrm {id}}_{\mathcal {K}}}{\mathbb {Z}}\cong (C\rtimes _\varphi {\mathbb {Z}})\otimes {\mathcal {K}}$
, and thus has the same K-groups as
$(C\otimes {\mathcal {K}})\rtimes _{\varphi \otimes {\mathrm {id}}_{\mathcal {K}}}{\mathbb {Z}}\cong (C\rtimes _\varphi {\mathbb {Z}})\otimes {\mathcal {K}}$
, and thus has the same K-groups as
![]() $C\rtimes _\varphi {\mathbb {Z}}$
. That is,
$C\rtimes _\varphi {\mathbb {Z}}$
. That is,
![]() $K_0(D)\cong K_1(D)\cong E$
.
$K_0(D)\cong K_1(D)\cong E$
.
Combining the above with (4.4), we deduce that
![]() $E\cong E\oplus E$
. This is, however, not the case: the largest divisible subgroup of E is
$E\cong E\oplus E$
. This is, however, not the case: the largest divisible subgroup of E is
![]() ${\mathbb {Q}}^2$
, while the largest divisible subgroup of
${\mathbb {Q}}^2$
, while the largest divisible subgroup of
![]() $E\oplus E$
is
$E\oplus E$
is
![]() ${\mathbb {Q}}^4$
. This contradiction shows that
${\mathbb {Q}}^4$
. This contradiction shows that
![]() $\varphi $
is aperiodic, proving the claim.
$\varphi $
is aperiodic, proving the claim.
Set
![]() $B=C\rtimes _\varphi {\mathbb {Z}}$
and
$B=C\rtimes _\varphi {\mathbb {Z}}$
and
![]() $\beta =\widehat {\varphi }\colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
. Then
$\beta =\widehat {\varphi }\colon {\mathbb {T}}\to {\mathrm {Aut}}(B)$
. Then
![]() $\beta $
has the Rokhlin property by Proposition 2.8, since
$\beta $
has the Rokhlin property by Proposition 2.8, since
![]() $\varphi $
is approximately representable. Moreover, B is unital, separable, nuclear, satisfies the UCT, and is simple since
$\varphi $
is approximately representable. Moreover, B is unital, separable, nuclear, satisfies the UCT, and is simple since
![]() $\varphi $
is aperiodic. Set
$\varphi $
is aperiodic. Set
![]() $A=B\otimes {\mathcal {O}_{\infty }}$
and
$A=B\otimes {\mathcal {O}_{\infty }}$
and
![]() $\alpha =\beta \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
. Then A is a unital Kirchberg algebra satisfying the UCT, and
$\alpha =\beta \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
. Then A is a unital Kirchberg algebra satisfying the UCT, and
![]() $\alpha $
has the Rokhlin property. Note that
$\alpha $
has the Rokhlin property. Note that
and thus
![]() $A^\alpha $
is the unique unital Kirchberg algebra satisfying the UCT with K-theory given by
$A^\alpha $
is the unique unital Kirchberg algebra satisfying the UCT with K-theory given by
![]() $K_0(A^\alpha )\cong K_1(A^\alpha )\cong K$
, with unit class
$K_0(A^\alpha )\cong K_1(A^\alpha )\cong K$
, with unit class
![]() $k_0$
.
$k_0$
.
We now wish to realize A in a different way as a crossed product by an approximately representable automorphism, in such a way such that the associated Pimsner–Voiculescu exact sequence splits into two copies of the trivial extension of K by itself.
Let
![]() $\psi _0\in {\mathrm {Aut}}({\mathcal {O}_{\infty }})$
be an aperiodic, approximately representable automorphism of
$\psi _0\in {\mathrm {Aut}}({\mathcal {O}_{\infty }})$
be an aperiodic, approximately representable automorphism of
![]() ${\mathcal {O}_{\infty }}$
(see, for example, Proposition 3.3 in [Reference Gardella11]). Set
${\mathcal {O}_{\infty }}$
(see, for example, Proposition 3.3 in [Reference Gardella11]). Set
![]() $\psi ={\mathrm {id}}_{A^\alpha }\otimes \psi _0$
, which we identify with an aperiodic, approximately representable automorphism of
$\psi ={\mathrm {id}}_{A^\alpha }\otimes \psi _0$
, which we identify with an aperiodic, approximately representable automorphism of
![]() $A^\alpha $
. Since
$A^\alpha $
. Since
![]() $K_1({\mathcal {O}_{\infty }})=0$
, both classes
$K_1({\mathcal {O}_{\infty }})=0$
, both classes
![]() $\eta _0(\psi _0)$
and
$\eta _0(\psi _0)$
and
![]() $\eta _1(\psi _0)$
are trivial. It follows that the same is true for
$\eta _1(\psi _0)$
are trivial. It follows that the same is true for
![]() $\eta _0(\psi )=\eta _1(\psi )=0$
in
$\eta _0(\psi )=\eta _1(\psi )=0$
in
![]() ${\mathrm {Ext}}(K,K)$
. The crossed product
${\mathrm {Ext}}(K,K)$
. The crossed product
![]() $A^\alpha \rtimes _\psi {\mathbb {Z}}$
is therefore a unital Kirchberg algebra satisfying the UCT with both K-groups isomorphic to E, and unit class
$A^\alpha \rtimes _\psi {\mathbb {Z}}$
is therefore a unital Kirchberg algebra satisfying the UCT with both K-groups isomorphic to E, and unit class
![]() $e_0$
. It follows from the classification of Kirchberg algebras (specifically Theorem 4.2.4 in [Reference Phillips35]) that there is an isomorphism
$e_0$
. It follows from the classification of Kirchberg algebras (specifically Theorem 4.2.4 in [Reference Phillips35]) that there is an isomorphism
![]() $A\cong A^\alpha \rtimes _\psi {\mathbb {Z}}$
. Denote by
$A\cong A^\alpha \rtimes _\psi {\mathbb {Z}}$
. Denote by
![]() $\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
the action that
$\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
the action that
![]() $\widehat {\psi }$
induces on A via this identification. Then
$\widehat {\psi }$
induces on A via this identification. Then
![]() $\gamma $
has the Rokhlin property because
$\gamma $
has the Rokhlin property because
![]() $\psi $
is approximately representable. Moreover,
$\psi $
is approximately representable. Moreover,
It follows that
![]() $K_\ast ^{\mathbb {T}}(A,\alpha )\cong K^{\mathbb {T}}_\ast (A,\gamma )$
as groups (in fact,
$K_\ast ^{\mathbb {T}}(A,\alpha )\cong K^{\mathbb {T}}_\ast (A,\gamma )$
as groups (in fact,
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
have isomorphic crossed products and fixed point algebras). This group isomorphism is automatically an isomorphism of
$\gamma $
have isomorphic crossed products and fixed point algebras). This group isomorphism is automatically an isomorphism of
![]() $R({\mathbb {T}})$
-modules, since the action of
$R({\mathbb {T}})$
-modules, since the action of
![]() $R({\mathbb {T}})\cong {\mathbb {Z}}[x,x^{-1}]$
on
$R({\mathbb {T}})\cong {\mathbb {Z}}[x,x^{-1}]$
on
![]() $K_\ast ^{\mathbb {T}}$
is determined by the dual automorphism, which for Rokhlin actions is approximately inner (by Proposition 2.8) and hence trivial on K-theory.
$K_\ast ^{\mathbb {T}}$
is determined by the dual automorphism, which for Rokhlin actions is approximately inner (by Proposition 2.8) and hence trivial on K-theory.
We denote by
![]() $\iota ^\alpha \colon A^\alpha \to A$
and
$\iota ^\alpha \colon A^\alpha \to A$
and
![]() $\iota ^\gamma \colon A^\alpha \to A$
the induced inclusions of
$\iota ^\gamma \colon A^\alpha \to A$
the induced inclusions of
![]() $A^\alpha $
into A as the
$A^\alpha $
into A as the
![]() $\alpha $
- and
$\alpha $
- and
![]() $\gamma $
-fixed point algebras, respectively.
$\gamma $
-fixed point algebras, respectively.
Claim: there is no
![]() $KK^{\mathbb {T}}$
-equivalence (unital or otherwise) between
$KK^{\mathbb {T}}$
-equivalence (unital or otherwise) between
![]() $(A,\alpha )$
and
$(A,\alpha )$
and
![]() $(A,\gamma )$
. This argument is in part similar to the one used in the proof of Theorem 4.6. Arguing by contradiction, let us assume that there is a
$(A,\gamma )$
. This argument is in part similar to the one used in the proof of Theorem 4.6. Arguing by contradiction, let us assume that there is a
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $\rho \in KK^{\mathbb {T}}((A,\alpha ),(A,\gamma ))$
. Using the Baaj–Skandalis duality, we get a
$\rho \in KK^{\mathbb {T}}((A,\alpha ),(A,\gamma ))$
. Using the Baaj–Skandalis duality, we get a
![]() $KK^{\mathbb {Z}}$
-equivalence
$KK^{\mathbb {Z}}$
-equivalence
Since
![]() $(A\rtimes _\alpha {\mathbb {T}},\widehat {\alpha })\sim _{KK^{\mathbb {Z}}} (A^\alpha ,\check {\alpha })$
and
$(A\rtimes _\alpha {\mathbb {T}},\widehat {\alpha })\sim _{KK^{\mathbb {Z}}} (A^\alpha ,\check {\alpha })$
and
![]() $(A\rtimes _\alpha {\mathbb {T}},\widehat {\gamma })\sim _{KK^{\mathbb {Z}}} (A^\alpha ,\check {\gamma })$
by Takai duality, we identify
$(A\rtimes _\alpha {\mathbb {T}},\widehat {\gamma })\sim _{KK^{\mathbb {Z}}} (A^\alpha ,\check {\gamma })$
by Takai duality, we identify
![]() $\rho \rtimes {\mathbb {T}}$
with a
$\rho \rtimes {\mathbb {T}}$
with a
![]() $KK^{\mathbb {Z}}$
-equivalence
$KK^{\mathbb {Z}}$
-equivalence
Denote by
![]() $\mathcal {F}(\kappa )\in KK(A^\alpha ,A^\alpha )$
the
$\mathcal {F}(\kappa )\in KK(A^\alpha ,A^\alpha )$
the
![]() $KK$
-equivalence that
$KK$
-equivalence that
![]() $\kappa $
induces under the forgetful functor
$\kappa $
induces under the forgetful functor
![]() $KK^{\mathbb {Z}}\to KK$
. Similarly, we let
$KK^{\mathbb {Z}}\to KK$
. Similarly, we let
![]() $\mathcal {F}(\kappa \rtimes {\mathbb {Z}})\in KK(A,A)$
denote the
$\mathcal {F}(\kappa \rtimes {\mathbb {Z}})\in KK(A,A)$
denote the
![]() $KK$
-equivalence that
$KK$
-equivalence that
![]() $\kappa \rtimes {\mathbb {Z}}$
induces, which can be canonically identified with
$\kappa \rtimes {\mathbb {Z}}$
induces, which can be canonically identified with
![]() $\mathcal {F}(\rho )$
. By naturality of all the functors involved, there is a commutative diagram
$\mathcal {F}(\rho )$
. By naturality of all the functors involved, there is a commutative diagram

where the vertical maps are all group isomorphisms. Note that the horizontal short exact sequences are the Pimsner–Voiculescu sequences associated with
![]() $\check {\alpha }$
and
$\check {\alpha }$
and
![]() $\check {\gamma }$
, respectively, as in (4.2), and thus their
$\check {\gamma }$
, respectively, as in (4.2), and thus their
![]() $\mathrm {Ext}$
-classes are
$\mathrm {Ext}$
-classes are
![]() $\eta _1(\check {\alpha })$
and
$\eta _1(\check {\alpha })$
and
![]() $\eta _1(\check {\gamma })$
, respectively. Moreover,
$\eta _1(\check {\gamma })$
, respectively. Moreover,
![]() $\check {\alpha }=\varphi \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
and under the
$\check {\alpha }=\varphi \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
and under the
![]() $KK$
-equivalence
$KK$
-equivalence
![]() $C\sim _{KK}C\otimes {\mathcal {O}_{\infty }}$
induced by
$C\sim _{KK}C\otimes {\mathcal {O}_{\infty }}$
induced by
![]() ${\mathbb {C}}\sim _{KK}{\mathcal {O}_{\infty }}$
, the class
${\mathbb {C}}\sim _{KK}{\mathcal {O}_{\infty }}$
, the class
![]() $\eta _1(\check {\alpha })$
corresponds to
$\eta _1(\check {\alpha })$
corresponds to
![]() $\xi $
. Similarly,
$\xi $
. Similarly,
![]() $\check {\gamma }$
is conjugate to
$\check {\gamma }$
is conjugate to
![]() ${\mathrm {id}}_{A^\alpha }\otimes \psi _0\in {\mathrm {Aut}}(A^\alpha \otimes {\mathcal {O}_{\infty }})$
, which under the
${\mathrm {id}}_{A^\alpha }\otimes \psi _0\in {\mathrm {Aut}}(A^\alpha \otimes {\mathcal {O}_{\infty }})$
, which under the
![]() $KK$
-equivalence
$KK$
-equivalence
![]() $A^\alpha \sim _{KK}A^\alpha \otimes {\mathcal {O}_{\infty }}$
induced by
$A^\alpha \sim _{KK}A^\alpha \otimes {\mathcal {O}_{\infty }}$
induced by
![]() ${\mathbb {C}}\sim _{KK}{\mathcal {O}_{\infty }}$
, the class
${\mathbb {C}}\sim _{KK}{\mathcal {O}_{\infty }}$
, the class
![]() $\eta _1(\check {\gamma })$
corresponds to
$\eta _1(\check {\gamma })$
corresponds to
![]() $\eta _1({\mathrm {id}}_{A^\alpha })=0$
.
$\eta _1({\mathrm {id}}_{A^\alpha })=0$
.
Commutativity of (4.5) implies that
![]() $\xi =0$
, which is a contradiction. We conclude that
$\xi =0$
, which is a contradiction. We conclude that
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are not
$\gamma $
are not
![]() $KK^{\mathbb {T}}$
-equivalent. In particular,
$KK^{\mathbb {T}}$
-equivalent. In particular,
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are not conjugate.
$\gamma $
are not conjugate.
The above example shows an interesting phenomenon, worth putting into perspective. In Example 10.6 in [Reference Rosenberg and Schochet38], the authors construct two circle actions on commutative
![]() $C^*$
-algebras with isomorphic
$C^*$
-algebras with isomorphic
![]() $K^{\mathbb {T}}$
-theory, which are not
$K^{\mathbb {T}}$
-theory, which are not
![]() $KK^{\mathbb {T}}$
-equivalent. In their example, the underlying algebras are not even
$KK^{\mathbb {T}}$
-equivalent. In their example, the underlying algebras are not even
![]() $KK$
-equivalent, so the actions cannot be
$KK$
-equivalent, so the actions cannot be
![]() $KK^{\mathbb {T}}$
-equivalent. As informed to us by Schochet, there was until now no known example of two circle actions on the same
$KK^{\mathbb {T}}$
-equivalent. As informed to us by Schochet, there was until now no known example of two circle actions on the same
![]() $C^*$
-algebra, with isomorphic fixed point algebras and crossed products, all satisfying the UCT, and with isomorphic
$C^*$
-algebra, with isomorphic fixed point algebras and crossed products, all satisfying the UCT, and with isomorphic
![]() $K^{\mathbb {T}}$
-theory, that are not
$K^{\mathbb {T}}$
-theory, that are not
![]() $KK^{\mathbb {T}}$
-equivalent. Our construction provides such an example.
$KK^{\mathbb {T}}$
-equivalent. Our construction provides such an example.
Theorem 4.6 states that, for Rokhlin actions on UCT Kirchberg algebras, the class Ext(
![]() $\alpha )$
defined in part (1) of Theorem 3.3 is a complete invariant up to conjugacy. It is then natural to ask for a range result, namely, which Ext-classes arise from Rokhlin actions on UCT Kirchberg algebras. In the next result, we show that the only possible obstructions are the ones we obtained in Theorem 3.3, specifically that the extension is pure.
$\alpha )$
defined in part (1) of Theorem 3.3 is a complete invariant up to conjugacy. It is then natural to ask for a range result, namely, which Ext-classes arise from Rokhlin actions on UCT Kirchberg algebras. In the next result, we show that the only possible obstructions are the ones we obtained in Theorem 3.3, specifically that the extension is pure.
Theorem 4.8 Let
![]() $K_0$
and
$K_0$
and
![]() $K_1$
be abelian groups, let
$K_1$
be abelian groups, let
![]() $k_0\in K_0$
, and let
$k_0\in K_0$
, and let
![]() $\mathcal {E}_0\in {\mathrm {Ext}}(K_0,K_1)$
and
$\mathcal {E}_0\in {\mathrm {Ext}}(K_0,K_1)$
and
![]() $\mathcal {E}_1\in {\mathrm {Ext}}(K_1,K_0)$
be extensions. The following are equivalent:
$\mathcal {E}_1\in {\mathrm {Ext}}(K_1,K_0)$
be extensions. The following are equivalent:
-
(a) There is a Rokhlin action
 $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital UCT Kirchberg algebra A with
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
on a unital UCT Kirchberg algebra A with
 $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong (\mathcal {E}_0,\mathcal {E}_1,k_0)$
in the sense of Definition 4.5.
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])\cong (\mathcal {E}_0,\mathcal {E}_1,k_0)$
in the sense of Definition 4.5. -
(b)
 $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
 $\mathcal {E}_1$
are pure.
$\mathcal {E}_1$
are pure.
Proof That (a) implies (b) follows from part (1) of Theorem 3.3. Assume that (b) holds, and write
![]() $\mathcal {E}_0$
and
$\mathcal {E}_0$
and
![]() $\mathcal {E}_1$
explicitly as
$\mathcal {E}_1$
explicitly as
For
![]() $j=0,1$
, let
$j=0,1$
, let
![]() $(K_j^{(n)})_{n\in {\mathbb {N}}}$
be an increasing sequence of finitely generated subgroups of
$(K_j^{(n)})_{n\in {\mathbb {N}}}$
be an increasing sequence of finitely generated subgroups of
![]() $K_j$
whose union equals
$K_j$
whose union equals
![]() $K_j$
. Without loss of generality, we assume that
$K_j$
. Without loss of generality, we assume that
![]() $k_0$
belongs to
$k_0$
belongs to
![]() $K_0^{(n)}$
for all
$K_0^{(n)}$
for all
![]() $n\in {\mathbb {N}}$
. Fix
$n\in {\mathbb {N}}$
. Fix
![]() $j=0,1$
. Since
$j=0,1$
. Since
![]() $\mathcal {E}_j$
is pure, for every
$\mathcal {E}_j$
is pure, for every
![]() $n\in {\mathbb {N}}$
there exists a (necessarily finitely generated) subgroup
$n\in {\mathbb {N}}$
there exists a (necessarily finitely generated) subgroup
![]() $\widetilde {K}_{1-j}^{(n)}$
of
$\widetilde {K}_{1-j}^{(n)}$
of
![]() $G_j$
such that
$G_j$
such that
![]() $\pi _j$
restricts to an isomorphism
$\pi _j$
restricts to an isomorphism
![]() $\widetilde {K}_{1-j}^{(n)}\cong K_{1-j}^{(n)}$
.
$\widetilde {K}_{1-j}^{(n)}\cong K_{1-j}^{(n)}$
.
Let
![]() $G_j^{(n)}$
be the subgroup of
$G_j^{(n)}$
be the subgroup of
![]() $G_j$
generated by
$G_j$
generated by
![]() $\iota _j(K_j^{(n)})$
and
$\iota _j(K_j^{(n)})$
and
![]() $\widetilde {K}_{1-j}^{(n)}$
. We denote by
$\widetilde {K}_{1-j}^{(n)}$
. We denote by
![]() $\mathcal {E}_j^{(n)}$
the restricted short exact sequence
$\mathcal {E}_j^{(n)}$
the restricted short exact sequence
where the maps are the restrictions of the ones for
![]() $\mathcal {E}_j$
. Fix
$\mathcal {E}_j$
. Fix
![]() $n\in {\mathbb {N}}$
. Since
$n\in {\mathbb {N}}$
. Since
![]() $\mathcal {E}_j$
is pure and
$\mathcal {E}_j$
is pure and
![]() $G^{(n)}_j$
is finitely generated, it follows that
$G^{(n)}_j$
is finitely generated, it follows that
![]() $\mathcal {E}^{(n)}_j$
is isomorphic to the trivial extension. Thus there are isomorphisms
$\mathcal {E}^{(n)}_j$
is isomorphic to the trivial extension. Thus there are isomorphisms
Under the above identifications, let
be the induced injective map.
Given
![]() $n\in {\mathbb {N}}$
, let
$n\in {\mathbb {N}}$
, let
![]() $\widetilde {B}_{n}$
be a UCT Kirchberg algebra satisfying
$\widetilde {B}_{n}$
be a UCT Kirchberg algebra satisfying
Fix an aperiodic approximately representable automorphism
![]() $\Phi $
of
$\Phi $
of
![]() ${\mathcal {O}_{\infty }}$
.Footnote
3
Set
${\mathcal {O}_{\infty }}$
.Footnote
3
Set
![]() $B_n=\widetilde {B}_n\otimes {\mathcal {O}_{\infty }}$
and
$B_n=\widetilde {B}_n\otimes {\mathcal {O}_{\infty }}$
and
![]() $\varphi _n={\mathrm {id}}_{\widetilde {B}_n}\otimes \Phi \in {\mathrm {Aut}}(B_n)$
. Then
$\varphi _n={\mathrm {id}}_{\widetilde {B}_n}\otimes \Phi \in {\mathrm {Aut}}(B_n)$
. Then
![]() $\varphi _n$
is approximately representable and aperiodic. Set
$\varphi _n$
is approximately representable and aperiodic. Set
![]() $A_n=B_n\rtimes _{\varphi _n}{\mathbb {Z}}$
and let
$A_n=B_n\rtimes _{\varphi _n}{\mathbb {Z}}$
and let
![]() $\alpha ^{(n)}\colon {\mathbb {T}}\to {\mathrm {Aut}}(A_n)$
denote the dual action of
$\alpha ^{(n)}\colon {\mathbb {T}}\to {\mathrm {Aut}}(A_n)$
denote the dual action of
![]() $\varphi _n$
. Then
$\varphi _n$
. Then
![]() $A_n$
is a Kirchberg algebra satisfying the UCT by part (4) of Proposition 4.2, and
$A_n$
is a Kirchberg algebra satisfying the UCT by part (4) of Proposition 4.2, and
![]() $\alpha ^{(n)}$
has the Rokhlin property by Proposition 2.8. Since the K-theory of
$\alpha ^{(n)}$
has the Rokhlin property by Proposition 2.8. Since the K-theory of
![]() $A_n$
is finitely generated, it follows from part (3) of Theorem 3.3 that
$A_n$
is finitely generated, it follows from part (3) of Theorem 3.3 that
![]() ${\mathrm {Ext}}_\ast (\alpha ^{(n)})$
is isomorphic to the trivial extension, and hence
${\mathrm {Ext}}_\ast (\alpha ^{(n)})$
is isomorphic to the trivial extension, and hence
![]() $({\mathrm {Ext}}_\ast (\alpha ^{(n)}),k_0)\cong (\mathcal {E}_0^{(n)},\mathcal {E}_1^{(n)},k_0)$
.
$({\mathrm {Ext}}_\ast (\alpha ^{(n)}),k_0)\cong (\mathcal {E}_0^{(n)},\mathcal {E}_1^{(n)},k_0)$
.
Use Theorem 4.1.1 in [Reference Phillips35] to find a unital homomorphism
![]() $\widetilde {\theta }_n\colon \widetilde {B}_n \to \widetilde {B}_{n+1}$
inducing the canonical inclusion
$\widetilde {\theta }_n\colon \widetilde {B}_n \to \widetilde {B}_{n+1}$
inducing the canonical inclusion
at the level of K-theory. Set
![]() $\theta _n=\widetilde {\theta }_n\otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}\colon B_n \to B_{n+1}$
, and note that
$\theta _n=\widetilde {\theta }_n\otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}\colon B_n \to B_{n+1}$
, and note that
![]() $\theta _n$
is equivariant with respect to the automorphisms
$\theta _n$
is equivariant with respect to the automorphisms
![]() $\varphi _n$
and
$\varphi _n$
and
![]() $\varphi _{n+1}$
. Let
$\varphi _{n+1}$
. Let
![]() $\rho _n\colon (A_n,\alpha ^{(n)})\to (A_{n+1},\alpha ^{(n+1)})$
be the unital equivariant homomorphism induced by
$\rho _n\colon (A_n,\alpha ^{(n)})\to (A_{n+1},\alpha ^{(n+1)})$
be the unital equivariant homomorphism induced by
![]() $\theta _n$
using duality.
$\theta _n$
using duality.
Finally, we set
![]() $(A,\alpha )=\varinjlim (A_n,\rho _n,\alpha ^{(n)})$
. Then A is a Kirchberg algebra satisfying the UCT, and
$(A,\alpha )=\varinjlim (A_n,\rho _n,\alpha ^{(n)})$
. Then A is a Kirchberg algebra satisfying the UCT, and
![]() $\alpha $
has the Rokhlin property by part (4) of Theorem 2.5 in [Reference Gardella12]. Since
$\alpha $
has the Rokhlin property by part (4) of Theorem 2.5 in [Reference Gardella12]. Since
![]() $K_j(\rho _n)$
is identified with
$K_j(\rho _n)$
is identified with
![]() $h_j^{(n)}\colon G_j^{(n)}\to G_j^{(n+1)}$
, it follows that
$h_j^{(n)}\colon G_j^{(n)}\to G_j^{(n+1)}$
, it follows that
![]() $\rho _n$
induces an embedding
$\rho _n$
induces an embedding
![]() $\mathcal {E}_j^{(n)}\hookrightarrow \mathcal {E}_j^{(n+1)}$
. Since the direct limit of
$\mathcal {E}_j^{(n)}\hookrightarrow \mathcal {E}_j^{(n+1)}$
. Since the direct limit of
![]() $\big (\mathcal {E}_j^{(n)},\rho _n\big )_{n\in {\mathbb {N}}}$
is isomorphic to
$\big (\mathcal {E}_j^{(n)},\rho _n\big )_{n\in {\mathbb {N}}}$
is isomorphic to
![]() $\mathcal {E}_j$
, we conclude that
$\mathcal {E}_j$
, we conclude that
![]() $({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])=(\mathcal {E}_0,\mathcal {E}_1,k_0)$
, as desired.
$({\mathrm {Ext}}_\ast (\alpha ),[1_{A^\alpha }])=(\mathcal {E}_0,\mathcal {E}_1,k_0)$
, as desired.
The following consequence of Theorems 4.6 and 4.8 will be needed later.
Corollary 4.9 Up to conjugacy, there exists a unique circle action on
![]() ${\mathcal {O}_2}$
with the Rokhlin property.
${\mathcal {O}_2}$
with the Rokhlin property.
We turn to Theorems F of the introduction, relating Rokhlin actions on arbitrary
![]() $C^*$
-algebras with Rokhlin actions on Kirchberg algebras. We will need to consider a specific automorphism of
$C^*$
-algebras with Rokhlin actions on Kirchberg algebras. We will need to consider a specific automorphism of
![]() ${\mathcal {O}_2}$
; its explicit description will be crucial in the proof of Theorem 4.15.
${\mathcal {O}_2}$
; its explicit description will be crucial in the proof of Theorem 4.15.
Notation 4.10 For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $u_n\in M_n\cong {\mathcal {B}}(\ell ^2(\{0,\ldots ,n-1\}))$
be the unitary given by
$u_n\in M_n\cong {\mathcal {B}}(\ell ^2(\{0,\ldots ,n-1\}))$
be the unitary given by
![]() $u_n(\delta _j)=\delta _{j+1}$
for
$u_n(\delta _j)=\delta _{j+1}$
for
![]() $j=0,\ldots ,n-1$
, where the subscripts are taken modulo n. (In particular,
$j=0,\ldots ,n-1$
, where the subscripts are taken modulo n. (In particular,
![]() $u_1=1\in {\mathbb {C}}$
.) Let
$u_1=1\in {\mathbb {C}}$
.) Let
![]() $\rho _n\colon M_n\to {\mathcal {O}_2}$
be a unital homomorphism. Fix an isomorphism
$\rho _n\colon M_n\to {\mathcal {O}_2}$
be a unital homomorphism. Fix an isomorphism
![]() $\kappa \colon \bigotimes _{n=1}^\infty {\mathcal {O}_2}\to {\mathcal {O}_2}$
, and let
$\kappa \colon \bigotimes _{n=1}^\infty {\mathcal {O}_2}\to {\mathcal {O}_2}$
, and let
![]() $\Psi \in {\mathrm {Aut}}({\mathcal {O}_2})$
be the automorphism satisfying
$\Psi \in {\mathrm {Aut}}({\mathcal {O}_2})$
be the automorphism satisfying
![]() $\Psi \circ \kappa =\kappa \circ \bigotimes _{n=1}^\infty {\mathrm {Ad}}(\rho _n(u_n))$
. One can check with elementary methods that
$\Psi \circ \kappa =\kappa \circ \bigotimes _{n=1}^\infty {\mathrm {Ad}}(\rho _n(u_n))$
. One can check with elementary methods that
![]() $\Psi $
is aperiodic.
$\Psi $
is aperiodic.
There exist by now a few equivariant
![]() $\mathcal {O}_2$
-embedding results; see, for example, Proposition 5.3 in [Reference Szabo42] or Theorem 4.8 in [Reference Gabe and Szabo7]. We need a more precise version of this embedding result in order to use it in the proof of Theorem 4.15, so we prove it next.
$\mathcal {O}_2$
-embedding results; see, for example, Proposition 5.3 in [Reference Szabo42] or Theorem 4.8 in [Reference Gabe and Szabo7]. We need a more precise version of this embedding result in order to use it in the proof of Theorem 4.15, so we prove it next.
Proposition 4.11 Let B be a unital, separable, exact
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\varphi \in {\mathrm {Aut}}(B)$
be an approximately inner automorphism. Then there exist a unitary
$\varphi \in {\mathrm {Aut}}(B)$
be an approximately inner automorphism. Then there exist a unitary
![]() $v\in {\mathcal {O}_2}$
and a unital, equivariant embedding
$v\in {\mathcal {O}_2}$
and a unital, equivariant embedding
![]() $(B,\varphi )\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
.
$(B,\varphi )\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
.
Moreover, the unitary v can be chosen so that there is a unital, equivariant embedding
![]() $({\mathcal {O}_2},{\mathrm {id}}_{\mathcal {O}_2})\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
.
$({\mathcal {O}_2},{\mathrm {id}}_{\mathcal {O}_2})\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
.
Proof Fix a unital embedding
![]() $\theta \colon B\to {\mathcal {O}_2}$
. Denote by
$\theta \colon B\to {\mathcal {O}_2}$
. Denote by
![]() $\pi \colon \ell ^\infty ({\mathcal {O}_2})\to ({\mathcal {O}_2})_\infty $
the canonical quotient map. Let
$\pi \colon \ell ^\infty ({\mathcal {O}_2})\to ({\mathcal {O}_2})_\infty $
the canonical quotient map. Let
![]() $(u_n)_{n\in {\mathbb {N}}}$
be any sequence of unitaries in B satisfying
$(u_n)_{n\in {\mathbb {N}}}$
be any sequence of unitaries in B satisfying
![]() $\varphi (b)=\lim \limits _{n\to \infty } {\mathrm {Ad}}(u_n)(b)$
for all
$\varphi (b)=\lim \limits _{n\to \infty } {\mathrm {Ad}}(u_n)(b)$
for all
![]() $b\in B$
, and set
$b\in B$
, and set
![]() $z=\pi \big ((\theta (u_n))_{n\in {\mathbb {N}}}\big )\in ({\mathcal {O}_2})_\infty $
. Then the unitary z satisfies
$z=\pi \big ((\theta (u_n))_{n\in {\mathbb {N}}}\big )\in ({\mathcal {O}_2})_\infty $
. Then the unitary z satisfies
![]() $\varphi (b)=z\theta (b)z^*$
for all
$\varphi (b)=z\theta (b)z^*$
for all
![]() $b\in B$
. By the universal property of the crossed product, there exists a unital embedding
$b\in B$
. By the universal property of the crossed product, there exists a unital embedding
![]() $\Theta \colon B\rtimes _{\varphi }{\mathbb {Z}}\to ({\mathcal {O}_2})_\infty $
.
$\Theta \colon B\rtimes _{\varphi }{\mathbb {Z}}\to ({\mathcal {O}_2})_\infty $
.
We will show that
![]() $\Theta $
lifts to a unital completely positive map
$\Theta $
lifts to a unital completely positive map
![]() $B\rtimes _\varphi {\mathbb {Z}}\to \ell ^\infty ({\mathcal {O}_2})$
which agrees with
$B\rtimes _\varphi {\mathbb {Z}}\to \ell ^\infty ({\mathcal {O}_2})$
which agrees with
![]() $\theta $
on the canonical copy of B. Denote by
$\theta $
on the canonical copy of B. Denote by
![]() $u\in B\rtimes _{\varphi }{\mathbb {Z}}$
the canonical unitary implementing
$u\in B\rtimes _{\varphi }{\mathbb {Z}}$
the canonical unitary implementing
![]() $\varphi $
For
$\varphi $
For
![]() $n\in {\mathbb {N}}$
, let
$n\in {\mathbb {N}}$
, let
![]() $\phi _n\colon B\rtimes _\varphi {\mathbb {Z}}\to M_n(B)$
and
$\phi _n\colon B\rtimes _\varphi {\mathbb {Z}}\to M_n(B)$
and
![]() $\psi _n\colon M_n(B)\to B\rtimes _\varphi {\mathbb {Z}}$
be the unital completely positive maps given as follows:
$\psi _n\colon M_n(B)\to B\rtimes _\varphi {\mathbb {Z}}$
be the unital completely positive maps given as follows:
 $$\begin{align*}\phi_n(bu^j)= \begin{cases} \sum\limits_{k=j}^{n-1}\varphi^{-k}(b)e_{k,k-j}, & \text{ if }0\leq j<n \\ \sum\limits_{k=0}^{j+n-1}\varphi^{-k}(b)e_{k,k-j}, & \text{ if } -n< j\leq 0\\ 0, & otherwise, \end{cases} \ \text{ and } \ \ \psi_n(b\otimes e_{j,k})=\frac{1}{n}\varphi^k(a)u^{k-j}. \end{align*}$$
$$\begin{align*}\phi_n(bu^j)= \begin{cases} \sum\limits_{k=j}^{n-1}\varphi^{-k}(b)e_{k,k-j}, & \text{ if }0\leq j<n \\ \sum\limits_{k=0}^{j+n-1}\varphi^{-k}(b)e_{k,k-j}, & \text{ if } -n< j\leq 0\\ 0, & otherwise, \end{cases} \ \text{ and } \ \ \psi_n(b\otimes e_{j,k})=\frac{1}{n}\varphi^k(a)u^{k-j}. \end{align*}$$
One readily checks that
![]() $\psi _n(\phi _n(bv^j))=\frac {n-j}{n}bv^j$
if
$\psi _n(\phi _n(bv^j))=\frac {n-j}{n}bv^j$
if
![]() $|j|< n$
, and
$|j|< n$
, and
![]() $0$
otherwise. In particular,
$0$
otherwise. In particular,
![]() $\psi _n\circ \phi _n$
converges pointwise in norm to
$\psi _n\circ \phi _n$
converges pointwise in norm to
![]() ${\mathrm {id}}_{B\rtimes _\varphi {\mathbb {Z}}}$
, and thus
${\mathrm {id}}_{B\rtimes _\varphi {\mathbb {Z}}}$
, and thus
![]() $\Theta \circ \psi _n\circ \phi _n$
converges pointwise in norm to
$\Theta \circ \psi _n\circ \phi _n$
converges pointwise in norm to
![]() $\Theta $
. Since
$\Theta $
. Since
![]() $B\rtimes _\varphi {\mathbb {Z}}$
is separable, it follows from Theorem 6 in [Reference Arveson2] that the set of maps
$B\rtimes _\varphi {\mathbb {Z}}$
is separable, it follows from Theorem 6 in [Reference Arveson2] that the set of maps
![]() $B\rtimes _\varphi {\mathbb {Z}}\to ({\mathcal {O}_2})_\infty $
which have unital completely positive lifts into
$B\rtimes _\varphi {\mathbb {Z}}\to ({\mathcal {O}_2})_\infty $
which have unital completely positive lifts into
![]() $\ell ^\infty ({\mathcal {O}_2})$
is closed in the point-norm topology. In particular, it suffices to show that for every
$\ell ^\infty ({\mathcal {O}_2})$
is closed in the point-norm topology. In particular, it suffices to show that for every
![]() $n\in {\mathbb {N}}$
, the map
$n\in {\mathbb {N}}$
, the map
![]() $\Theta \circ \psi _n\circ \phi _n$
has a unital completely positive lift which extends
$\Theta \circ \psi _n\circ \phi _n$
has a unital completely positive lift which extends
![]() $\theta $
.
$\theta $
.
Using nuclearity of
![]() $M_n$
, let
$M_n$
, let
![]() $\widetilde {\rho }_n\colon M_n\to \ell ^\infty ({\mathcal {O}_2})$
be any unital completely positive lift of the composition
$\widetilde {\rho }_n\colon M_n\to \ell ^\infty ({\mathcal {O}_2})$
be any unital completely positive lift of the composition
Let
![]() $\rho _n\colon M_n(B) \to \ell ^\infty ({\mathcal {O}_2})$
be the linear map determined by
$\rho _n\colon M_n(B) \to \ell ^\infty ({\mathcal {O}_2})$
be the linear map determined by
for all
![]() $b\in B$
and
$b\in B$
and
![]() $j,k=0,\ldots ,n-1$
. Then
$j,k=0,\ldots ,n-1$
. Then
![]() $\rho _n$
is unital. We claim that
$\rho _n$
is unital. We claim that
![]() $\rho _n$
is positive. Since a positive element in
$\rho _n$
is positive. Since a positive element in
![]() $M_n(B)$
is the sum of n elements of the form
$M_n(B)$
is the sum of n elements of the form
![]() $\sum _{j,k=0}^{n-1} b_j^*b_k\otimes e_{j,k}$
for some
$\sum _{j,k=0}^{n-1} b_j^*b_k\otimes e_{j,k}$
for some
![]() $b_0,\ldots ,b_{n-1}\in B$
, it suffices to show that
$b_0,\ldots ,b_{n-1}\in B$
, it suffices to show that
![]() $\rho _n$
preserves positivity of such elements. Given
$\rho _n$
preserves positivity of such elements. Given
![]() $b_0,\ldots ,b_{n-1}\in B$
, set
$b_0,\ldots ,b_{n-1}\in B$
, set
 $$\begin{align*}b=\sum_{j,k=0}^{n-1} b_j^*b_k\otimes e_{j,k}\in M_n(B) \ \ \mbox{ and } \ \ x=\sum_{j=0}^{n-1}\theta(b_j)\widetilde{\rho}_n(e_{j,j})^{1/2}\in \ell^\infty({\mathcal{O}_2}).\end{align*}$$
$$\begin{align*}b=\sum_{j,k=0}^{n-1} b_j^*b_k\otimes e_{j,k}\in M_n(B) \ \ \mbox{ and } \ \ x=\sum_{j=0}^{n-1}\theta(b_j)\widetilde{\rho}_n(e_{j,j})^{1/2}\in \ell^\infty({\mathcal{O}_2}).\end{align*}$$
Then
![]() $\rho _n(b)=x^*x\geq 0$
, as desired. It follows that
$\rho _n(b)=x^*x\geq 0$
, as desired. It follows that
![]() $\rho _n$
is positive, and one shows in a similar way that it is completely positive.
$\rho _n$
is positive, and one shows in a similar way that it is completely positive.
Note that
![]() $\pi \circ \rho _n=\Theta \circ \psi _n$
, and this
$\pi \circ \rho _n=\Theta \circ \psi _n$
, and this
![]() $\rho _n\circ \phi _n$
is a lift for
$\rho _n\circ \phi _n$
is a lift for
![]() $\Theta \circ \psi _n\circ \phi _n$
which agrees with
$\Theta \circ \psi _n\circ \phi _n$
which agrees with
![]() $\theta $
on the canonical copy of B. Thus there exists a unital completely positive lift for
$\theta $
on the canonical copy of B. Thus there exists a unital completely positive lift for
![]() $\Theta $
which extends
$\Theta $
which extends
![]() $\theta $
.
$\theta $
.
Using Lemma 2.2 in [Reference Kirchberg and Phillips20], find a unital embedding
![]() $\sigma \colon B\rtimes _{\varphi }{\mathbb {Z}}\to {\mathcal {O}_2}$
satisfying
$\sigma \colon B\rtimes _{\varphi }{\mathbb {Z}}\to {\mathcal {O}_2}$
satisfying
![]() $\sigma (b)=\theta (b)$
for all
$\sigma (b)=\theta (b)$
for all
![]() $b\in B$
, and set
$b\in B$
, and set
![]() $w=\sigma (u)$
. Consider the following embeddings, where the first one is the restriction of
$w=\sigma (u)$
. Consider the following embeddings, where the first one is the restriction of
![]() $\sigma $
to B:
$\sigma $
to B:
Note that
![]() ${\mathrm {Ad}}(w)$
is unitarily equivalent to
${\mathrm {Ad}}(w)$
is unitarily equivalent to
![]() ${\mathrm {id}}_{{\mathcal {O}_2}}$
, and that
${\mathrm {id}}_{{\mathcal {O}_2}}$
, and that
![]() ${\mathrm {id}}_{{\mathcal {O}_2}}\otimes \Psi $
is conjugate to
${\mathrm {id}}_{{\mathcal {O}_2}}\otimes \Psi $
is conjugate to
![]() $\Psi $
. It follows that
$\Psi $
. It follows that
![]() ${\mathrm {Ad}}(w)\otimes \Psi $
is unitarily equivalent to
${\mathrm {Ad}}(w)\otimes \Psi $
is unitarily equivalent to
![]() ${\mathrm {id}}_{\mathcal {O}_2}\otimes \Psi $
of
${\mathrm {id}}_{\mathcal {O}_2}\otimes \Psi $
of
![]() ${\mathcal {O}_2}\cong {\mathcal {O}_2}\otimes {\mathcal {O}_2}$
. Since
${\mathcal {O}_2}\cong {\mathcal {O}_2}\otimes {\mathcal {O}_2}$
. Since
![]() ${\mathrm {id}}_{\mathcal {O}_2}\otimes \Psi $
is conjugate to
${\mathrm {id}}_{\mathcal {O}_2}\otimes \Psi $
is conjugate to
![]() $\Psi $
, and thus there is a unital, equivariant embedding
$\Psi $
, and thus there is a unital, equivariant embedding
![]() $(B,\varphi )\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
for some unitary
$(B,\varphi )\to ({\mathcal {O}_2},{\mathrm {Ad}}(v)\circ \Psi )$
for some unitary
![]() $v\in {\mathcal {O}_2}$
.
$v\in {\mathcal {O}_2}$
.
Since
![]() $({\mathcal {O}_2},{\mathrm {id}}_{{\mathcal {O}_2}})$
embeds unitally into
$({\mathcal {O}_2},{\mathrm {id}}_{{\mathcal {O}_2}})$
embeds unitally into
![]() $({\mathcal {O}_2}, \Psi )$
, it follows that is also embeds unitally into
$({\mathcal {O}_2}, \Psi )$
, it follows that is also embeds unitally into
![]() $({\mathcal {O}_2}\otimes {\mathcal {O}_2},{\mathrm {Ad}}(w)\otimes \Psi )$
. Thus the last part of the statement also follows from the construction above.
$({\mathcal {O}_2}\otimes {\mathcal {O}_2},{\mathrm {Ad}}(w)\otimes \Psi )$
. Thus the last part of the statement also follows from the construction above.
As a byproduct of the proposition above, we can easily deduce a
![]() $\mathbb {T}$
-equivariant version of Kirchberg’s
$\mathbb {T}$
-equivariant version of Kirchberg’s
![]() $\mathcal {O}_2$
-embedding theorem. It should be pointed out that there are other ways of proving this which even apply to all compact groups (see Remark 4.13). We thus do not claim the corollary below to be really new, or as general as it could possibly be.
$\mathcal {O}_2$
-embedding theorem. It should be pointed out that there are other ways of proving this which even apply to all compact groups (see Remark 4.13). We thus do not claim the corollary below to be really new, or as general as it could possibly be.
Corollary 4.12 Let A be a unital, separable, exact
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Denote by
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Denote by
![]() $\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}({\mathcal {O}_2})$
the unique action with the Rokhlin property (see Corollary 4.9). Then there exists a unital, equivariant embedding
$\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}({\mathcal {O}_2})$
the unique action with the Rokhlin property (see Corollary 4.9). Then there exists a unital, equivariant embedding
![]() $(A,\alpha ) \hookrightarrow ({\mathcal {O}_2},\gamma )$
.
$(A,\alpha ) \hookrightarrow ({\mathcal {O}_2},\gamma )$
.
Proof Note that
![]() $A^\alpha $
is unital, separable and exact, and that the predual automorphism
$A^\alpha $
is unital, separable and exact, and that the predual automorphism
![]() $\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
is approximately inner by Proposition 2.8. Use Proposition 4.11 to find a unitary
$\check {\alpha }\in {\mathrm {Aut}}(A^\alpha )$
is approximately inner by Proposition 2.8. Use Proposition 4.11 to find a unitary
![]() $v\in {\mathcal {O}_2}$
and a unital embedding
$v\in {\mathcal {O}_2}$
and a unital embedding
Set
![]() $\Phi ={\mathrm {Ad}}(u)\circ \Psi $
. Since
$\Phi ={\mathrm {Ad}}(u)\circ \Psi $
. Since
![]() $\Psi $
is aperiodic, the same is true for
$\Psi $
is aperiodic, the same is true for
![]() $\Phi $
. It follows from parts (3) and (4) of Proposition 4.2 that
$\Phi $
. It follows from parts (3) and (4) of Proposition 4.2 that
![]() ${\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}}$
is a Kirchberg algebra satisfying the UCT, and it has trivial K-theory by the Pimsner–Voiculescu exact sequence. Thus
${\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}}$
is a Kirchberg algebra satisfying the UCT, and it has trivial K-theory by the Pimsner–Voiculescu exact sequence. Thus
![]() ${\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}}$
is isomorphic to
${\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}}$
is isomorphic to
![]() ${\mathcal {O}_2}$
. Moreover, since
${\mathcal {O}_2}$
. Moreover, since
![]() $\Psi $
is approximately representable by construction, the same is true for
$\Psi $
is approximately representable by construction, the same is true for
![]() $\Phi $
. By Proposition 2.8, it follows that the dual action
$\Phi $
. By Proposition 2.8, it follows that the dual action
![]() $\widehat {\Phi }$
has the Rokhlin property, and thus
$\widehat {\Phi }$
has the Rokhlin property, and thus
![]() $\widehat {\Phi }$
is conjugate to
$\widehat {\Phi }$
is conjugate to
![]() $\gamma $
by Corollary 4.9.
$\gamma $
by Corollary 4.9.
Applying crossed products to (4.7), and identifying
![]() $(A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}},\widehat {\check {\alpha }})$
with
$(A^\alpha \rtimes _{\check {\alpha }}{\mathbb {Z}},\widehat {\check {\alpha }})$
with
![]() $(A,\alpha )$
(see Theorem 2.3), and identifying
$(A,\alpha )$
(see Theorem 2.3), and identifying
![]() $({\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}},\widehat {\Phi })$
with
$({\mathcal {O}_2}\rtimes _\Phi {\mathbb {Z}},\widehat {\Phi })$
with
![]() $({\mathcal {O}_2},\gamma )$
as in the paragraph above, we obtain a unital homomorphism
$({\mathcal {O}_2},\gamma )$
as in the paragraph above, we obtain a unital homomorphism
![]() $\widetilde {\iota }\colon (A,\alpha )\to ({\mathcal {O}_2},\gamma )$
. Finally,
$\widetilde {\iota }\colon (A,\alpha )\to ({\mathcal {O}_2},\gamma )$
. Finally,
![]() $\widetilde {\iota }$
is injective because so is
$\widetilde {\iota }$
is injective because so is
![]() $\iota $
and
$\iota $
and
![]() ${\mathbb {Z}}$
is amenable.
${\mathbb {Z}}$
is amenable.
Remark 4.13 We point out that it is possible to give a simpler proof of Corollary 4.12 which avoids Proposition 4.11, by applying Lemma 4.7 in [Reference Arano and Kubota1] to any embedding
![]() $A\hookrightarrow {\mathcal {O}_2}$
. This argument even has the advantage of working for arbitrary compact groups. We have taken a more indirect approach because Corollary 4.12 by itself is not enough to prove Theorem 4.15, and in its proof we will need to use Proposition 4.11 instead.
$A\hookrightarrow {\mathcal {O}_2}$
. This argument even has the advantage of working for arbitrary compact groups. We have taken a more indirect approach because Corollary 4.12 by itself is not enough to prove Theorem 4.15, and in its proof we will need to use Proposition 4.11 instead.
Recall that a homomorphism
![]() $\pi \colon A\to B$
is said to be full if for every
$\pi \colon A\to B$
is said to be full if for every
![]() $a\in A$
with
$a\in A$
with
![]() ${a\neq 0}$
, the ideal in B generated by
${a\neq 0}$
, the ideal in B generated by
![]() $\pi (a)$
is all of B. If
$\pi (a)$
is all of B. If
![]() $\varphi \in {\mathrm {Aut}}(A)$
and
$\varphi \in {\mathrm {Aut}}(A)$
and
![]() $\psi \in {\mathrm {Aut}}(B)$
satisfy
$\psi \in {\mathrm {Aut}}(B)$
satisfy
![]() $\psi \circ \pi =\pi \circ \varphi $
, then the
$\psi \circ \pi =\pi \circ \varphi $
, then the
![]() ${\mathbb {T}}$
-equivariant homomorphism
${\mathbb {T}}$
-equivariant homomorphism
![]() $\widehat {\pi }\colon A\rtimes _\varphi {\mathbb {Z}} \to B\rtimes _\psi {\mathbb {Z}}$
induced by
$\widehat {\pi }\colon A\rtimes _\varphi {\mathbb {Z}} \to B\rtimes _\psi {\mathbb {Z}}$
induced by
![]() $\pi $
is full if and only if so is
$\pi $
is full if and only if so is
![]() $\pi $
.
$\pi $
.
The following easy observation will be used in the proof of Theorem 4.15.
Remark 4.14 If
![]() $(A_n,\pi _n)_{n\in {\mathbb {N}}}$
is an inductive system and
$(A_n,\pi _n)_{n\in {\mathbb {N}}}$
is an inductive system and
![]() $\pi _n$
is full for every
$\pi _n$
is full for every
![]() $n\in {\mathbb {N}}$
, then
$n\in {\mathbb {N}}$
, then
![]() $\varinjlim (A_n,\pi _n)$
is simple.
$\varinjlim (A_n,\pi _n)$
is simple.
We are ready to show that every Rokhlin action on a separable, nuclear
![]() $C^*$
-algebra is
$C^*$
-algebra is
![]() $KK^{\mathbb {T}}$
-equivalent to a Rokhlin action on a Kirchberg algebra. Our proof roughly follows arguments of Kirchberg, specifically as in Chapter 11 of [Reference Kirchberg19]. However, we need to make the choices carefully and perform some computations in equivariant
$KK^{\mathbb {T}}$
-equivalent to a Rokhlin action on a Kirchberg algebra. Our proof roughly follows arguments of Kirchberg, specifically as in Chapter 11 of [Reference Kirchberg19]. However, we need to make the choices carefully and perform some computations in equivariant
![]() $KK^{\mathbb {T}}$
-theory using the continuous Rokhlin property from [Reference Gardella11], in order to guarantee that the resulting action on the Kirchberg algebra has the Rokhlin property. (We do not seem to be able to guarantee this using the Cuntz–Pimsner construction from Theorem 2.1 in [Reference Meyer27].)
$KK^{\mathbb {T}}$
-theory using the continuous Rokhlin property from [Reference Gardella11], in order to guarantee that the resulting action on the Kirchberg algebra has the Rokhlin property. (We do not seem to be able to guarantee this using the Cuntz–Pimsner construction from Theorem 2.1 in [Reference Meyer27].)
Theorem 4.15 Let A be a separable, nuclear unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there exist a unital Kirchberg algebra D and a circle action
$\alpha \colon {\mathbb {T}}\to {\mathrm {Aut}}(A)$
be an action with the Rokhlin property. Then there exist a unital Kirchberg algebra D and a circle action
![]() $\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
with the Rokhlin property, such that
$\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
with the Rokhlin property, such that
![]() $(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
unitally.
$(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
unitally.
Proof Let
![]() $v\in {\mathcal {O}_2}$
be a unitary as in the conclusion of Corollary 4.12, and set
$v\in {\mathcal {O}_2}$
be a unitary as in the conclusion of Corollary 4.12, and set
![]() $\Phi ={\mathrm {Ad}}(v)\circ \Psi $
. Fix unital embeddings
$\Phi ={\mathrm {Ad}}(v)\circ \Psi $
. Fix unital embeddings
We prove the theorem in two steps. First, assume that there is a unital equivariant embedding
![]() $\sigma \colon ({\mathcal {O}_2},\Phi )\to (A^\alpha ,\check {\alpha })$
. Let
$\sigma \colon ({\mathcal {O}_2},\Phi )\to (A^\alpha ,\check {\alpha })$
. Let
![]() $s_1,s_2\in \mathcal {O}_2$
be the canonical generating isometries, and note that
$s_1,s_2\in \mathcal {O}_2$
be the canonical generating isometries, and note that
![]() $\tau (s_1)$
and
$\tau (s_1)$
and
![]() $\tau (s_2)$
are
$\tau (s_2)$
are
![]() $\Phi $
-invariant. Set
$\Phi $
-invariant. Set
![]() $t_j=\sigma (\tau (s_j))$
for
$t_j=\sigma (\tau (s_j))$
for
![]() $j=1,2$
. Then
$j=1,2$
. Then
![]() $t_j$
is an isometry,
$t_j$
is an isometry,
![]() $\check {\alpha }(t_j)=t_j$
, and
$\check {\alpha }(t_j)=t_j$
, and
![]() $t_1t_1^*+t_2t_2^*=1$
. Define a unital equivariant map
$t_1t_1^*+t_2t_2^*=1$
. Define a unital equivariant map
![]() $\pi \colon (A^\alpha ,\check {\alpha })\to (A^\alpha ,\check {\alpha })$
by
$\pi \colon (A^\alpha ,\check {\alpha })\to (A^\alpha ,\check {\alpha })$
by
for all
![]() $a\in A^\alpha $
. Then
$a\in A^\alpha $
. Then
![]() $\pi $
is full. Indeed, if
$\pi $
is full. Indeed, if
![]() $a\in A^\alpha \setminus \{0\}$
, then
$a\in A^\alpha \setminus \{0\}$
, then
![]() $\rho (a)\neq 0$
and thus pure infiniteness of
$\rho (a)\neq 0$
and thus pure infiniteness of
![]() ${\mathcal {O}_2}$
implies that there exist
${\mathcal {O}_2}$
implies that there exist
![]() $x,y\in {\mathcal {O}_2}$
with
$x,y\in {\mathcal {O}_2}$
with
![]() $x\rho (a)y=1_{\mathcal {O}_2}$
. Then
$x\rho (a)y=1_{\mathcal {O}_2}$
. Then
and thus
![]() $\pi (a)$
generates
$\pi (a)$
generates
![]() $A^\alpha $
as an ideal, as desired.
$A^\alpha $
as an ideal, as desired.
Claim 1
We have
![]() $KK^{\mathbb {Z}}(\pi )=KK^{\mathbb {Z}}({\mathrm {id}}_{A^\alpha })$
. By Theorem F in the introduction of [Reference Gardella11] (see also Corollary 3.10 there), the action
$KK^{\mathbb {Z}}(\pi )=KK^{\mathbb {Z}}({\mathrm {id}}_{A^\alpha })$
. By Theorem F in the introduction of [Reference Gardella11] (see also Corollary 3.10 there), the action
![]() $\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}({\mathcal {O}_2})$
has the continuous Rokhlin property, and thus it is unitally
$\gamma \colon {\mathbb {T}}\to {\mathrm {Aut}}({\mathcal {O}_2})$
has the continuous Rokhlin property, and thus it is unitally
![]() $KK^{\mathbb {T}}$
-equivalent to
$KK^{\mathbb {T}}$
-equivalent to
![]() $\big (C({\mathbb {T}})\otimes {\mathcal {O}_2},\texttt {Lt}\otimes {\mathrm {id}}_{{\mathcal {O}_2}}\big )$
by Theorem C of [Reference Gardella11]. By Baaj–Skandalis duality, and since the dual of
$\big (C({\mathbb {T}})\otimes {\mathcal {O}_2},\texttt {Lt}\otimes {\mathrm {id}}_{{\mathcal {O}_2}}\big )$
by Theorem C of [Reference Gardella11]. By Baaj–Skandalis duality, and since the dual of
![]() $\gamma $
is
$\gamma $
is
![]() $KK^{\mathbb {Z}}$
-equivalent to
$KK^{\mathbb {Z}}$
-equivalent to
![]() $\Phi $
, we deduce that
$\Phi $
, we deduce that
![]() $({\mathcal {O}_2},\Phi )$
is
$({\mathcal {O}_2},\Phi )$
is
![]() $KK^{\mathbb {Z}}$
-equivalent to
$KK^{\mathbb {Z}}$
-equivalent to
![]() $({\mathcal {O}_2},{\mathrm {id}}_{{\mathcal {O}_2}})$
. Thus
$({\mathcal {O}_2},{\mathrm {id}}_{{\mathcal {O}_2}})$
. Thus
Since
![]() $\sigma \circ \rho $
factors through
$\sigma \circ \rho $
factors through
![]() $({\mathcal {O}_2},\Phi )$
, it must be
$({\mathcal {O}_2},\Phi )$
, it must be
![]() $KK^{\mathbb {Z}}$
-trivial. We conclude that
$KK^{\mathbb {Z}}$
-trivial. We conclude that
![]() $KK^{\mathbb {Z}}(\pi )=KK^{\mathbb {Z}}({\mathrm {id}}_{A^\alpha })$
.
$KK^{\mathbb {Z}}(\pi )=KK^{\mathbb {Z}}({\mathrm {id}}_{A^\alpha })$
.
We deduce from the claim above that
![]() $\pi $
is a
$\pi $
is a
![]() $KK^{\mathbb {Z}}$
-equivalence, and that
$KK^{\mathbb {Z}}$
-equivalence, and that
![]() $\widehat {\pi }$
is a
$\widehat {\pi }$
is a
![]() $KK^{\mathbb {T}}$
-equivalence. Set
$KK^{\mathbb {T}}$
-equivalence. Set
![]() $(C_0,\theta _0)=\varinjlim \big ((A^\alpha ,\check {\alpha }),\pi \big )$
. Then
$(C_0,\theta _0)=\varinjlim \big ((A^\alpha ,\check {\alpha }),\pi \big )$
. Then
![]() $C_0$
is simple because
$C_0$
is simple because
![]() $\pi $
is full (see Remark 4.14), and it is nuclear, unital and separable because so is
$\pi $
is full (see Remark 4.14), and it is nuclear, unital and separable because so is
![]() $A^\alpha $
. Denote by
$A^\alpha $
. Denote by
![]() $\Pi \colon (A^\alpha , \check {\alpha })\to (C_0,\theta _0)$
the canonical equivariant map into the limit.
$\Pi \colon (A^\alpha , \check {\alpha })\to (C_0,\theta _0)$
the canonical equivariant map into the limit.
Claim 2
![]() $\Pi $
is a
$\Pi $
is a
![]() $KK^{\mathbb {Z}}$
-equivalence. (This is not immediate from Claim 1, since
$KK^{\mathbb {Z}}$
-equivalence. (This is not immediate from Claim 1, since
![]() $KK^{\mathbb {Z}}$
is not a continuous functor.) By the second paragraph on page 287 of [Reference Meyer and Nest29], it suffices to show that the class
$KK^{\mathbb {Z}}$
is not a continuous functor.) By the second paragraph on page 287 of [Reference Meyer and Nest29], it suffices to show that the class
![]() $\mathcal {F}(\Pi )\in KK(A^\alpha , C_0)$
that
$\mathcal {F}(\Pi )\in KK(A^\alpha , C_0)$
that
![]() $\Pi $
induces under the forgetful functor
$\Pi $
induces under the forgetful functor
![]() $\mathcal {F}$
, is a
$\mathcal {F}$
, is a
![]() $KK$
-equivalence. This is contained in Kirchberg’s proof (specifically Sections 11.2 and 11.3 in [Reference Kirchberg19]) there), so the claim follows.
$KK$
-equivalence. This is contained in Kirchberg’s proof (specifically Sections 11.2 and 11.3 in [Reference Kirchberg19]) there), so the claim follows.
Set
![]() $(C,\theta )=(C\otimes {\mathcal {O}_{\infty }},\theta _0\otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}})$
. Then C is a unital Kirchberg algebra, and
$(C,\theta )=(C\otimes {\mathcal {O}_{\infty }},\theta _0\otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}})$
. Then C is a unital Kirchberg algebra, and
![]() $(C,\theta )\sim _{KK^{\mathbb {Z}}}(A^\alpha ,\check {\alpha })$
unitally, since
$(C,\theta )\sim _{KK^{\mathbb {Z}}}(A^\alpha ,\check {\alpha })$
unitally, since
![]() $({\mathcal {O}_{\infty }},{\mathrm {id}}_{{\mathcal {O}_{\infty }}})\sim _{KK^{\mathbb {Z}}}({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})$
unitally.
$({\mathcal {O}_{\infty }},{\mathrm {id}}_{{\mathcal {O}_{\infty }}})\sim _{KK^{\mathbb {Z}}}({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})$
unitally.
Claim 3
![]() $\theta $
is aperiodic and approximately representable. It suffices to prove the claim for
$\theta $
is aperiodic and approximately representable. It suffices to prove the claim for
![]() $\theta _0$
. Since
$\theta _0$
. Since
![]() $(C_0,\theta _0)$
is the direct limit of
$(C_0,\theta _0)$
is the direct limit of
![]() $(A^\alpha ,\check {\alpha })$
and
$(A^\alpha ,\check {\alpha })$
and
![]() $\check {\alpha }$
is approximately representable, it follows that so is
$\check {\alpha }$
is approximately representable, it follows that so is
![]() $\theta _0$
. Note that there is an isomorphism
$\theta _0$
. Note that there is an isomorphism
![]() $C_0=\varinjlim (A,\widehat {\pi })$
. Let
$C_0=\varinjlim (A,\widehat {\pi })$
. Let
![]() $\widehat {\pi }\colon (A,\alpha )\to (A,\alpha )$
be the map induced by
$\widehat {\pi }\colon (A,\alpha )\to (A,\alpha )$
be the map induced by
![]() $\pi $
. Then
$\pi $
. Then
![]() $\widehat {\pi }$
is full, because so is
$\widehat {\pi }$
is full, because so is
![]() $\pi $
. It therefore follows from Remark 4.14 that
$\pi $
. It therefore follows from Remark 4.14 that
![]() $C_0$
is simple. By part (1) of Proposition 4.2, we deduce that
$C_0$
is simple. By part (1) of Proposition 4.2, we deduce that
![]() $\theta _0$
is aperiodic.
$\theta _0$
is aperiodic.
Set
![]() $D=C\rtimes _\theta {\mathbb {Z}}$
and
$D=C\rtimes _\theta {\mathbb {Z}}$
and
![]() $\delta =\widehat {\theta }$
. Since C is a Kirchberg algebra and
$\delta =\widehat {\theta }$
. Since C is a Kirchberg algebra and
![]() $\theta $
is aperiodic, it follows from part (3) of Proposition 4.2 that D is a unital Kirchberg algebra. Moreover,
$\theta $
is aperiodic, it follows from part (3) of Proposition 4.2 that D is a unital Kirchberg algebra. Moreover,
![]() $\delta $
has the Rokhlin property by Proposition 2.8, since
$\delta $
has the Rokhlin property by Proposition 2.8, since
![]() $\theta $
is approximately representable by Claim 3. Finally, by Claim 2, the equivariant map
$\theta $
is approximately representable by Claim 3. Finally, by Claim 2, the equivariant map
![]() $\Pi \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
is a unital
$\Pi \otimes {\mathrm {id}}_{{\mathcal {O}_{\infty }}}$
is a unital
![]() $KK^{\mathbb {Z}}$
-equivalent
$KK^{\mathbb {Z}}$
-equivalent
![]() $(A^\alpha ,\check {\alpha })\sim _{KK^{\mathbb {Z}}} (C,\theta )$
. By taking crossed products, we obtain a unital
$(A^\alpha ,\check {\alpha })\sim _{KK^{\mathbb {Z}}} (C,\theta )$
. By taking crossed products, we obtain a unital
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
. This proves the theorem in the case that there is a unital equivariant embedding
$(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
. This proves the theorem in the case that there is a unital equivariant embedding
![]() $\sigma \colon ({\mathcal {O}_2},\Phi )\to (A^\alpha ,\check {\alpha })$
.
$\sigma \colon ({\mathcal {O}_2},\Phi )\to (A^\alpha ,\check {\alpha })$
.
We turn to the general case. Let
![]() $\mathcal {O}_\infty ^{(0)}$
be the unique unital UCT Kirchberg algebra which is
$\mathcal {O}_\infty ^{(0)}$
be the unique unital UCT Kirchberg algebra which is
![]() $KK$
-equivalent to
$KK$
-equivalent to
![]() ${\mathcal {O}_{\infty }}$
and whose class of the unit is zero.
${\mathcal {O}_{\infty }}$
and whose class of the unit is zero.
Claim 4
There exists an automorphism
![]() $\psi \in {\mathrm {Aut}}(\mathcal {O}_\infty )$
which leaves a copy of
$\psi \in {\mathrm {Aut}}(\mathcal {O}_\infty )$
which leaves a copy of
![]() $\mathcal {O}^{(0)}_\infty $
invariant, and such that with
$\mathcal {O}^{(0)}_\infty $
invariant, and such that with
![]() $\varphi \in {\mathrm {Aut}}(\mathcal {O}^{(0)}_\infty )$
denoting its restriction,
$\varphi \in {\mathrm {Aut}}(\mathcal {O}^{(0)}_\infty )$
denoting its restriction,
![]() $\varphi $
is aperiodic and admits and a unital equivariant embedding
$\varphi $
is aperiodic and admits and a unital equivariant embedding
![]() $\iota \colon ({\mathcal {O}_2},\Phi )\hookrightarrow (\mathcal {O}_\infty ^{(0)},\varphi )$
. Fix an injective homomorphism
$\iota \colon ({\mathcal {O}_2},\Phi )\hookrightarrow (\mathcal {O}_\infty ^{(0)},\varphi )$
. Fix an injective homomorphism
![]() $\nu \colon {\mathcal {O}_2}\to {\mathcal {O}_{\infty }}$
, and set
$\nu \colon {\mathcal {O}_2}\to {\mathcal {O}_{\infty }}$
, and set
![]() $p=1_{\mathcal {O}_{\infty }}-\nu (1)$
, which is a projection in
$p=1_{\mathcal {O}_{\infty }}-\nu (1)$
, which is a projection in
![]() ${\mathcal {O}_{\infty }}$
. Adopt the notation of Notation 4.10, in particular, we will use the unital homomorphisms
${\mathcal {O}_{\infty }}$
. Adopt the notation of Notation 4.10, in particular, we will use the unital homomorphisms
![]() $\rho _n\colon M_n\to {\mathcal {O}_2}$
and the permutation unitaries
$\rho _n\colon M_n\to {\mathcal {O}_2}$
and the permutation unitaries
![]() $u_n\in M_n$
. For
$u_n\in M_n$
. For
![]() $n\in {\mathbb {N}}$
, set
$n\in {\mathbb {N}}$
, set
![]() $w_n=\nu (\rho _n(u_n))+p$
, which is a unitary in
$w_n=\nu (\rho _n(u_n))+p$
, which is a unitary in
![]() ${\mathcal {O}_{\infty }}$
. Consider the automorphism
${\mathcal {O}_{\infty }}$
. Consider the automorphism
![]() $\widetilde {\psi }= \bigotimes _{n=1}^\infty {\mathrm {Ad}}(w_n)$
of
$\widetilde {\psi }= \bigotimes _{n=1}^\infty {\mathrm {Ad}}(w_n)$
of
![]() $\bigotimes _{n=1}^\infty {\mathcal {O}_{\infty }}$
, and note that the restriction of
$\bigotimes _{n=1}^\infty {\mathcal {O}_{\infty }}$
, and note that the restriction of
![]() $\widetilde {\psi }$
to the invariant subalgebra
$\widetilde {\psi }$
to the invariant subalgebra
![]() $\bigotimes _{n=0}^\infty \nu ({\mathcal {O}_2})$
can be identified with
$\bigotimes _{n=0}^\infty \nu ({\mathcal {O}_2})$
can be identified with
![]() $\bigotimes _{n=1}^\infty {\mathrm {Ad}}(\rho _n(u_n))$
. Fix an isomorphism
$\bigotimes _{n=1}^\infty {\mathrm {Ad}}(\rho _n(u_n))$
. Fix an isomorphism
![]() $\widetilde {\kappa }\colon \bigotimes _{n=1}^\infty {\mathcal {O}_{\infty }}\to {\mathcal {O}_{\infty }}$
, and let
$\widetilde {\kappa }\colon \bigotimes _{n=1}^\infty {\mathcal {O}_{\infty }}\to {\mathcal {O}_{\infty }}$
, and let
![]() $\mu \colon {\mathcal {O}_2}\to {\mathcal {O}_{\infty }}$
be the following composition:
$\mu \colon {\mathcal {O}_2}\to {\mathcal {O}_{\infty }}$
be the following composition:

Set
![]() $w=\mu (v)$
and
$w=\mu (v)$
and
![]() $\psi =\widetilde {\kappa }\circ {\mathrm {Ad}}(w)\circ \widetilde {\psi }\circ \widetilde {\kappa }^{-1}\in {\mathrm {Aut}}({\mathcal {O}_{\infty }})$
. Set
$\psi =\widetilde {\kappa }\circ {\mathrm {Ad}}(w)\circ \widetilde {\psi }\circ \widetilde {\kappa }^{-1}\in {\mathrm {Aut}}({\mathcal {O}_{\infty }})$
. Set
![]() $e=\mu (1)$
, which is a projection in
$e=\mu (1)$
, which is a projection in
![]() ${\mathcal {O}_{\infty }}$
satisfying
${\mathcal {O}_{\infty }}$
satisfying
![]() $\psi (e)=e$
and
$\psi (e)=e$
and
![]() $[e]=0$
in
$[e]=0$
in
![]() $K_0({\mathcal {O}_{\infty }})\cong {\mathbb {Z}}$
. In particular, there is an injective homomorphism
$K_0({\mathcal {O}_{\infty }})\cong {\mathbb {Z}}$
. In particular, there is an injective homomorphism
![]() $j\colon \mathcal {O}_{\infty }^{(0)}\to {\mathcal {O}_{\infty }}$
whose image is
$j\colon \mathcal {O}_{\infty }^{(0)}\to {\mathcal {O}_{\infty }}$
whose image is
![]() $e{\mathcal {O}_{\infty }} e$
. Note that
$e{\mathcal {O}_{\infty }} e$
. Note that
![]() $\psi $
leaves the image of j invariant. Then
$\psi $
leaves the image of j invariant. Then
![]() $\mu (v)$
is a unitary in
$\mu (v)$
is a unitary in
![]() $e{\mathcal {O}_{\infty }} e$
, and we let
$e{\mathcal {O}_{\infty }} e$
, and we let
![]() $\varphi \in {\mathrm {Aut}}(\mathcal {O}_{\infty }^{(0)})$
be given by
$\varphi \in {\mathrm {Aut}}(\mathcal {O}_{\infty }^{(0)})$
be given by
![]() $\varphi =j^{-1}\circ \psi \circ j$
. Let
$\varphi =j^{-1}\circ \psi \circ j$
. Let
![]() $\iota \colon {\mathcal {O}_2}\to \mathcal {O}_{\infty }^{(0)}$
be the unital homomorphism given by
$\iota \colon {\mathcal {O}_2}\to \mathcal {O}_{\infty }^{(0)}$
be the unital homomorphism given by
![]() $\iota =j^{-1}\circ \mu $
. One readily checks that
$\iota =j^{-1}\circ \mu $
. One readily checks that
![]() $\varphi $
and
$\varphi $
and
![]() $\iota $
satisfy the conditions in the claim.
$\iota $
satisfy the conditions in the claim.
Claim 5
Any automorphism
![]() $\varphi \in {\mathrm {Aut}}(\mathcal {O}_\infty ^{(0)})$
satisfying the conclusion of Claim 4 satisfies
$\varphi \in {\mathrm {Aut}}(\mathcal {O}_\infty ^{(0)})$
satisfying the conclusion of Claim 4 satisfies
![]() $(\mathcal {O}_\infty ^{(0)},\varphi )\sim _{KK^{\mathbb {Z}}} ({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})$
. Note that there are unital, equivariant homomorphisms
$(\mathcal {O}_\infty ^{(0)},\varphi )\sim _{KK^{\mathbb {Z}}} ({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})$
. Note that there are unital, equivariant homomorphisms
![]() $(\mathcal {O}^{(0)}_\infty ,\varphi )\to ({\mathcal {O}_{\infty }},\psi )$
and
$(\mathcal {O}^{(0)}_\infty ,\varphi )\to ({\mathcal {O}_{\infty }},\psi )$
and
![]() $({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})\to ({\mathcal {O}_{\infty }},\psi )$
. Both of these are
$({\mathbb {C}},{\mathrm {id}}_{\mathbb {C}})\to ({\mathcal {O}_{\infty }},\psi )$
. Both of these are
![]() $KK$
-equivalences, and thus they are
$KK$
-equivalences, and thus they are
![]() $KK^{\mathbb {Z}}$
-equivalences by the second paragraph on page 287 of [Reference Meyer and Nest29].
$KK^{\mathbb {Z}}$
-equivalences by the second paragraph on page 287 of [Reference Meyer and Nest29].
Let
![]() $\varphi \in {\mathrm {Aut}}(\mathcal {O}_\infty ^{(0)})$
be as in the conclusion of Claim 4. Then clearly there is a unital equivariant embedding of
$\varphi \in {\mathrm {Aut}}(\mathcal {O}_\infty ^{(0)})$
be as in the conclusion of Claim 4. Then clearly there is a unital equivariant embedding of
![]() $({\mathcal {O}_2},\Phi )$
into
$({\mathcal {O}_2},\Phi )$
into
![]() $(A^\alpha \otimes \mathcal {O}_\infty ^{(0)},\check {\alpha }\otimes \varphi )$
. Using the first part of this proof, let
$(A^\alpha \otimes \mathcal {O}_\infty ^{(0)},\check {\alpha }\otimes \varphi )$
. Using the first part of this proof, let
![]() $\delta _0\colon {\mathbb {T}}\to {\mathrm {Aut}}(D_0)$
be an action with the Rokhlin property on a unital Kirchberg algebra
$\delta _0\colon {\mathbb {T}}\to {\mathrm {Aut}}(D_0)$
be an action with the Rokhlin property on a unital Kirchberg algebra
![]() $D_0$
such that
$D_0$
such that
![]() $(D_0,\delta _0)$
is
$(D_0,\delta _0)$
is
![]() $KK^{\mathbb {T}}$
-equivalent to the dual system of
$KK^{\mathbb {T}}$
-equivalent to the dual system of
![]() $(A^\alpha \otimes \mathcal {O}_\infty ^{(0)},\check {\alpha }\otimes \varphi )$
. Said dual system is
$(A^\alpha \otimes \mathcal {O}_\infty ^{(0)},\check {\alpha }\otimes \varphi )$
. Said dual system is
![]() $KK^{\mathbb {T}}$
-equivalent to
$KK^{\mathbb {T}}$
-equivalent to
![]() $(A,\alpha )$
by Claim 5, and thus there is a
$(A,\alpha )$
by Claim 5, and thus there is a
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $\eta \in KK^{\mathbb {T}}\big ((A,\alpha ),(D_0,\delta _0)\big )$
. Since
$\eta \in KK^{\mathbb {T}}\big ((A,\alpha ),(D_0,\delta _0)\big )$
. Since
![]() $\delta _0$
has the Rokhlin property, by Corollary 2.5 there is a canonical isomorphism
$\delta _0$
has the Rokhlin property, by Corollary 2.5 there is a canonical isomorphism
![]() $K_0(D_0\rtimes _{\delta _0}{\mathbb {T}})\cong K_0(D_0^{\delta _0})$
. Combining this with the natural group isomorphism
$K_0(D_0\rtimes _{\delta _0}{\mathbb {T}})\cong K_0(D_0^{\delta _0})$
. Combining this with the natural group isomorphism
![]() $K_0^{\mathbb {T}}(D_0,\delta _0)\cong K_0(D_0\rtimes _{\delta _0}{\mathbb {T}})$
given by Julg’s theorem, it follows that there is a natural identification
$K_0^{\mathbb {T}}(D_0,\delta _0)\cong K_0(D_0\rtimes _{\delta _0}{\mathbb {T}})$
given by Julg’s theorem, it follows that there is a natural identification
![]() $K_0^{\mathbb {T}}(D_0,\delta _0)\cong K_0(D_0^{\delta _0})$
. Since
$K_0^{\mathbb {T}}(D_0,\delta _0)\cong K_0(D_0^{\delta _0})$
. Since
![]() $D_0^{\delta _0}$
is a Kirchberg algebra by part (3) of Proposition 4.2, any element of its
$D_0^{\delta _0}$
is a Kirchberg algebra by part (3) of Proposition 4.2, any element of its
![]() $K_0$
-group can be realized by a projection in
$K_0$
-group can be realized by a projection in
![]() $D_0^{\delta _0}$
. It follows that there exists a projection
$D_0^{\delta _0}$
. It follows that there exists a projection
![]() $q\in D_0^{\delta _0}$
such that
$q\in D_0^{\delta _0}$
such that
![]() $[1_A]\times \eta =[q]$
in
$[1_A]\times \eta =[q]$
in
![]() $K_0^{\mathbb {T}}(D_0,\delta _0)$
. Set
$K_0^{\mathbb {T}}(D_0,\delta _0)$
. Set
![]() $D=qD_0q$
and let
$D=qD_0q$
and let
![]() $\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
denote the restriction of
$\delta \colon {\mathbb {T}}\to {\mathrm {Aut}}(D)$
denote the restriction of
![]() $\delta _0$
to D. Then D is a unital Kirchberg algebra, and
$\delta _0$
to D. Then D is a unital Kirchberg algebra, and
![]() $\delta $
has the Rokhlin property by part (3) of Theorem 2.5 in [Reference Gardella12]. Finally, it is clear that
$\delta $
has the Rokhlin property by part (3) of Theorem 2.5 in [Reference Gardella12]. Finally, it is clear that
![]() $\eta $
implements a unital
$\eta $
implements a unital
![]() $KK^{\mathbb {T}}$
-equivalence
$KK^{\mathbb {T}}$
-equivalence
![]() $(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
, as desired.
$(A,\alpha )\sim _{KK^{\mathbb {T}}}(D,\delta )$
, as desired.
Acknowledgments
The author is grateful to a number of people for helpful discussions, correspondence, or feedback, including Claude Schochet, Rasmus Bentmann, Martino Lupini, Ralf Meyer, Chris Phillips, and Hannes Thiel.