Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-22T09:25:46.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Bounds for Torsion Points on Abelian Varieties

Published online by Cambridge University Press:  20 November 2018

Pete L. Clark  and
Xavier Xarles
Pete L. Clark
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA 30602, U.S.A. e-mail:, pete@math.uga.edu
Xavier Xarles
Affiliation:
Departament de Matemátiques, Universitsat Autónoma de Barcelona, Catahunya, Spain e-mail:, xarles@mat.uab.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

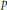We say that an abelian variety over a $p$-adic field 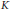$K$ has anisotropic reduction 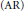$(\text{AR})$ if the special fiber of its Néron minimal model does not contain a nontrivial split torus. This includes all abelian varieties with potentially good reduction and, in particular, those with complex or quaternionic multiplication. We give a bound for the size of the 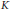$K$-rational torsion subgroup of a 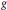$g$-dimensional 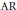$\text{AR}$ variety depending only on 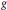$g$ and the numerical invariants of 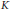$K$ (the absolute ramification index and the cardinality of the residue field). Applying these bounds to abelian varieties over a number field with everywhere locally anisotropic reduction, we get bounds which, as a function of 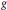$g$, are close to optimal. In particular, we determine the possible cardinalities of the torsion subgroup of an 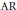$\text{AR}$ abelian surface over the rational numbers, up to a set of 11 values which are not known to occur. The largest such value is 72.

Keywords

11G1014K15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 532 - 555
Copyright
Copyright © Canadian Mathematical Society 2008

References

[BLR] Bosch, S., Lütkebohmert, W., and Raynaud, M., Néron models. Ergebnisse derMathematik und ihrer Grenzgebiete 21, Springer-Verlag, Berlin, 1990.Google Scholar
[BX] Bosch, S. and Xarles, X., Component groups of Néron models via rigid uniformization. Math. Ann. 306(1996), no. 3, 459–486.Google Scholar
[Bu] Buzzard, K., Integral models of certain Shimura curves. Duke Math. J. 87(1997), no. 3, 591–612.Google Scholar
[Cl] Clark, P., Rational points on Atkin-Lehner quotients of Shimura curves. Thesis, Harvard University, 2003.Google Scholar
[DH] DiPippo, S. and Howe, E., Real polynomials with all roots on the unit circle and abelian varieties over finite fields. J. Number Theory 73(1998), no. 2, 426–450.Google Scholar
[Ed] Edixhoven, S., On the prime-to-p part of the groups of connected components of Néron models. Compositio Math. 97(1995), no. 1-2, 29–49.Google Scholar
[ELL] Edixhoven, S., Liu, Q., and Lorenzini, D., The p-part of the group of components of a Néron model. J. Algebraic Geom. 5(1996), no. 4, 801–813.Google Scholar
[FO] Flexor, M. and Oesterl, J.é, Sur les points de torsion des courbes elliptiques. In: Séminaire sur les Pinceaux de Courbes Elliptiques, Astérisque 1990 no. 193, pp. 25–36.Google Scholar
[Fr] Frey, G., Some remarks concerning points of finite order on elliptic curves over global fields. Ark. Mat. 15(1977), no. 1, 1–19.Google Scholar
[HS] Hindry, M. and Silverman, J., Sur le nombre de points de torsion rationnels sur une courbe elliptique. C. R. Acad. Sci. Paris Sér. I Math. 329(1999), no. 2, 97–100.Google Scholar
[Kub] Kubert, D., Universal bounds on the torsion of elliptic curves. Proc. LondonMath. Soc. 33(1976), no. 2, 193–237.Google Scholar
[LO] Lenstra, H. W., Jr. and Oort, F., Abelian varieties having purely additive reduction. J. Pure Appl. Algebra 36(1985), no. 3, 281–298.Google Scholar
[Lo1] Lorenzini, D., Jacobians with potentially good ℓ-reduction. J. Reine Angew.Math. 430(1992), 151–177.Google Scholar
[Lo2] Lorenzini, D., On the group of components of a Néron model. J. Reine Angew.Math. 445(1993), 109–160.Google Scholar
[MT] Mazur, B. and Tate, J., Points of order 13 on elliptic curves. Invent.Math. 22(1973/74), 41–49.Google Scholar
[Me] Merel, L., Bornes pour la torsion des courbes elliptiques sur les corps de nombres. Invent.Math. 124(1996), no. 1-3, 437–449.Google Scholar
[Mi] Minkowski, H., Zur Theorie der positiven quadratische Formen. J. Reine Angew.Math. 101(1887), 196–202.Google Scholar
[MSZ] Müller, H., Ströher, H., and Zimmer, H., Torsion groups of elliptic curves with integral j-invariant over quadratic felds. J. Reine Angew.Math. 397(1989), 100–161.Google Scholar
[Ol] Olson, L., Points of finite order on elliptic curves with complex multiplication. ManuscriptaMath. 14(1974), 195–205.Google Scholar
[PY] Prasad, D. and Yogananda, C. S., Bounding the torsion in CM elliptic curves. C. R. Math. Acad. Sci. Soc. R. Can. 23(2001), no. 1, 1–5.Google Scholar
[Se1] Serre, J.-P.. Corps locaux, Hermann, Paris, 1962.Google Scholar
[Se2] Serre, J.-P., Algebraic Groups and Class Fields. Graduate Texts in Mathematics 117, Springer-Verlag, New York, 1988.Google Scholar
[Se3] Serre, J.-P., Lie Algebras and Lie Groups. Lecture Notes in Mathematics 1500, Springer-Verlag, Berlin, 1992.Google Scholar
[ST] Serre, J.-P. and Tate, J., Good reduction of abelian varieties. Ann. of Math. 88(1968), 492–517.Google Scholar
[Sg1] Silverberg, A., Torsion points on abelian varieties of CM-type. Compositio Math. 68(1988), no. 3, 241–249.Google Scholar
[Sg2] Silverberg, A., Points of finite order on abelian varieties. Contemp.Math. 133(1992), 175–193.Google Scholar
[Sg3] Silverberg, A., Open questions in arithmetic algebraic geometry. In: Arithmetic Algebraic Geometry. IAS/Park CityMath. Ser. 9, American Mathematical Society, Providence, RI, 2001, pp. 83–142.Google Scholar
[Si1] Silverman, J., The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 106, Springer-Verlag, New York, 1986.Google Scholar
[Si2] Silverman, J., Advanced Topics in The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics 151, Springer-Verlag, New York, 1994.Google Scholar
[VanM] Van Mulbregt, P., Torsion-points on low-dimensional abelian varieties with complex multiplication. Contemp.Math. 133(1992), 205–210,Google Scholar
[Wa] Waterhouse, W. C., Abelian varieties over finite fields. Ann. Sci. école Norm. Sup. 2(1969), 521–560.Google Scholar
[Xa] Xarles, X., The scheme of connected components of the Néron model of an algebraic torus. J. Reine Angew.Math. 437(1993), 167–179.Google Scholar