Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-29T21:17:05.360Z Has data issue: false hasContentIssue false
  • English
  • Français

Loops in the fundamental group of 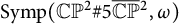${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions

Part of: Differential topology Symplectic geometry, contact geometry Homology and homotopy of topological groups and related structures

Published online by Cambridge University Press:  30 June 2022

Sílvia Anjos Open the ORCID record for Sílvia Anjos [Opens in a new window] ,
Miguel Barata ,
Martin Pinsonnault  and
Ana Alexandra Reis
Sílvia Anjos*
Affiliation:
Center for Mathematical Analysis, Geometry and Dynamical Systems, Department of Mathematics, Instituto Superior Técnico, Avenida Rovisco Pais, 1049-001 Lisboa, Portugal
Miguel Barata
Affiliation:
Utrecht Geometry Center, Utrecht University, Budapestlaan 6,3584 CD Utrecht, The Netherlands e-mail: m.lourencohenriquesbarata@uu.nl
Martin Pinsonnault
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON, Canada e-mail: mpinson@uwo.ca
Ana Alexandra Reis
Affiliation:
Department of Mathematics, Instituto Superior Técnico, Avenida Rovisco Pais, 1049-001 Lisboa, Portugal e-mail: ana.alexandra.reis@tecnico.ulisboa.pt
*
e-mail: sanjos@math.tecnico.ulisboa.pt
Get access Rights & Permissions [Opens in a new window]

Abstract

We study generators of the fundamental group of the group of symplectomorphisms 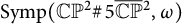$\operatorname {\mathrm{Symp}} (\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2, \omega )$ for some particular symplectic forms. It was observed by Kȩdra (2009, Archivum Mathematicum 45) that there are many symplectic 4-manifolds 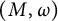$(M, \omega )$, where M is neither rational nor ruled, that admit no circle action and 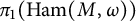$\pi _1 (\operatorname {\mathrm {Ham}} (M,\omega ))$ is nontrivial. On the other hand, it follows from Abreu and McDuff (2000, Journal of the American Mathematical Society 13, 971–1009), Anjos and Eden (2019, Michigan Mathematical Journal 68, 71–126), Anjos and Pinsonnault (2013, Mathematische Zeitschrift 275, 245–292), and Pinsonnault (2008, Compositio Mathematica 144, 787–810) that the fundamental group of the group 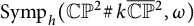$ \operatorname {\mathrm{Symp}}_h(\mathbb C\mathbb P^2\#\,k\overline { \mathbb C\mathbb P}\,\!^2,\omega )$, of symplectomorphisms that act trivially on homology, with 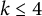$k \leq 4$, is generated by circle actions on the manifold. We show that, for some particular symplectic forms 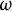$\omega $, the set of all Hamiltonian circle actions generates a proper subgroup in 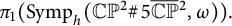$\pi _1(\operatorname {\mathrm{Symp}}_{h}(\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2,\omega )).$ Our work depends on Delzant classification of toric symplectic manifolds, Karshon’s classification of Hamiltonian 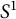$S^1$-spaces, and the computation of Seidel elements of some circle actions.

Keywords

symplectic geometrysymplectomorphism groupfundamental groupHamiltonian circle actions

MSC classification

Primary: 53D35: Global theory of symplectic and contact manifolds
Secondary: 57R17: Symplectic and contact topology 57S05: Topological properties of groups of homeomorphisms or diffeomorphisms 57T20: Homotopy groups of topological groups and homogeneous spaces

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 4 , August 2023 , pp. 1226 - 1271
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author is partially supported by FCT/Portugal through projects UID/MAT/04459/2019 and PTDC/MAT-PUR/29447/2017. The third author is partially supported by NSERC Discovery Grant RGPIN-2020-06428. All authors except the third are supported by the Calouste Gulbenkian Foundation through the program “New Talents in Mathematics.”

References

Abreu, M., Granja, G., and Kitchloo, N., Compatible complex structures on symplectic rational ruled surfaces . Duke Math. J. 148(2009), 539–600.10.1215/00127094-2009-033CrossRefGoogle Scholar
Abreu, M. and McDuff, D., Topology of symplectomorphism groups of rational ruled surfaces . J. Amer. Math. Soc. 13(2000), 971–1009.CrossRefGoogle Scholar
Anjos, S. and Eden, S., The homotopy Lie algebra of symplectomorphisms groups of 3-folds blow-ups of $\left({S}^2\times {S}^2,{\sigma}_{\mathrm{std}}\oplus {\sigma}_{\mathrm{std}}\right)$ . Michigan Math. J. 68(2019), no. 1, 71–126.10.1307/mmj/1547089467CrossRefGoogle Scholar
Anjos, S. and Leclercq, R., Seidel’s morphism of toric 4-manifolds . J. Symplectic Geom. 16(2018), no. 1, 1–68.CrossRefGoogle Scholar
Anjos, S. and Pinsonnault, M., The homotopy Lie algebra of symplectomorphism groups of 3-fold blow-ups of the projective plane . Math. Z. 275(2013), 245–292.10.1007/s00209-012-1134-5CrossRefGoogle Scholar
Buse, O., Negative inflation and stability in symplectomorphism groups of ruled surfaces . J. Symplectic Geom. 9(2011), no. 2, 147–160.10.4310/JSG.2011.v9.n2.a3CrossRefGoogle Scholar
Crauder, B. and Miranda, R., Quantum cohomology of rational surfaces . In: Dijkgraaf, R. H., Faber, C. F., and van der Geer, G. B. M. (eds.), The moduli space of curves. Progress in Mathematics, 129, Birkhäuser, Boston, 1995.Google Scholar
Delzant, T., Hamiltoniens périodiques et image convexe de l’application moment . Bull. Soc. Math. France 116(1988), 315–339.10.24033/bsmf.2100CrossRefGoogle Scholar
Evans, J. D., Symplectic mapping class groups of some Stein and rational surfaces . J. Symplectic Geom. 9(2011), no. 1, 45–82.10.4310/JSG.2011.v9.n1.a4CrossRefGoogle Scholar
Karshon, Y., Periodic Hamiltonian flows on four dimensional manifolds, Memoirs of the American Mathematical Society, 141, no. 672 (1999).10.1090/memo/0672CrossRefGoogle Scholar
Karshon, Y. and Kessler, L., Distinguishing symplectic blowups of the complex projective plane . J. Symplectic Geom. 15(2017), no. 4, 1089–1128.10.4310/JSG.2017.v15.n4.a5CrossRefGoogle Scholar
Karshon, Y., Kessler, L., and Pinsonnault, M., Counting Toric actions on symplectic four-manifolds . C. R. Math. Acad. Sci. Soc. R. Can. 37(2015), no. 1, 33–40.Google Scholar
Kȩdra, J., Fundamental group of $\ Symp(M,\omega)\,{}$ with no circle action . Arch. Math. (Brno) 45(2009), no. 1, 75–78.Google Scholar
Lalonde, F. and McDuff, D., The classification of ruled symplectic 4-manifolds . Math. Res. Lett. 3(1996), 769–778.10.4310/MRL.1996.v3.n6.a5CrossRefGoogle Scholar
Lalonde, F. and McDuff, D.. J-curves and the classification of rational and ruled symplectic 4-manifolds . In: Contact and symplectic geometry (Cambridge, 1994), Publications of the Newton Institute, 8, Cambridge University Press, Cambridge, 1996, pp. 3–42 (in English summary).Google Scholar
Li, J. and Li, T. J., Symplectic-2 spheres and the symplectomorphism group of small rational 4-manifolds . Pacific J. Math. 304(2020), no. 2, 561–606.10.2140/pjm.2020.304.561CrossRefGoogle Scholar
Li, J., Li, T. J., and Wu, W., The symplectic mapping class group of $\ {\mathbb{CP}}^2\#\mathrm{n}\overline{{\mathbb{CP}}^2\,}$ with $\ n\le 4$ . Michigan Math. J. 64(2015), no. 2, 319–333.CrossRefGoogle Scholar
Li, J., Li, T. J., and Wu, W., Symplectic-2 spheres and the symplectomorphism group of small rational 4-manifolds II . Trans. Amer. Math. Soc. 375(2022), no. 2, 1357–1410.Google Scholar
Li, T. J. and Liu, A., Symplectic structure on ruled surfaces and a generalized adjunction formula . Math. Res. Lett. 2(1995), no. 4, 453–471.CrossRefGoogle Scholar
Li, T. J. and Liu, A., Uniqueness of symplectic canonical class, surface cone and symplectic cone of 4-manifolds with $\ {b}^{+}=1$ . J. Differential Geom. 58(2001), no. 2, 331–370.10.4310/jdg/1090348329CrossRefGoogle Scholar
Li, T. J. and Wu, W., Lagrangian spheres, symplectic surfaces and the symplectic mapping class group . Geom. Topol. 16(2012), no. 2, 1121–1169.CrossRefGoogle Scholar
McDuff, D., From symplectic deformation to isotopy . In: Topics in symplectic 4-manifolds (Irvine, CA, 1996), International Press, Cambridge, MA, 1998, pp. 85–99.Google Scholar
McDuff, D. and Salamon, D. A., J-holomorphic curves and quantum cohomology. 2nd ed., American Mathematical Society Colloquium Publications, 52, American Mathematical Society, Providence, RI, 2012, xiv+726 pp.Google Scholar
McDuff, D. and Tolman, S., Topological properties of Hamiltonian circle actions . Int. Math. Res. Not. IMRN 2006(2006), 72826.Google Scholar
Pinsonnault, M., Symplectomorphism groups and embeddings of balls into rational ruled surfaces . Compos. Math. 144(2008), no. 3, 787–810.CrossRefGoogle Scholar
Pinsonnault, M., Maximal compact tori in the Hamiltonian group of 4-dimensional symplectic manifolds . J. Mod. Dyn. 2(2008), no. 3, 431–455.10.3934/jmd.2008.2.431CrossRefGoogle Scholar
Seidel, P., ${\pi}_1$ of symplectic automorphism groups and invertibles in quantum cohomology rings . Geom. Funct. Anal. 7(1997), 237–250.CrossRefGoogle Scholar
Seidel, P., Lectures on four-dimensional Dehn twists . In Symplectic 4-manifolds and algebraic surfaces, Lecture Notes in Mathematics, 1938, Springer, Berlin, 2008, pp. 231–267.CrossRefGoogle Scholar
Sternberg, S., Minimal coupling and the symplectic mechanics of a classical particle in the presence of a Yang–Mills field . Proc. Natl. Acad. Sci. USA 74, 5253–5254.CrossRefGoogle Scholar
Zhang, J., Symplectic structure perturbations and continuity of symplectic invariants . Algebr. Geom. Topol. 19(2019), no. 7, 3261–3314.CrossRefGoogle Scholar