No CrossRef data available.
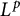 $L^p$-regularity of the Bergman projection on quotient domains
$L^p$-regularity of the Bergman projection on quotient domainsPublished online by Cambridge University Press: 08 February 2021
We obtain sharp ranges of 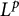 $L^p$
-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating
$L^p$
-boundedness for domains in a wide class of Reinhardt domains representable as sublevel sets of monomials, by expressing them as quotients of simpler domains. We prove a general transformation law relating 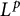 $L^p$
-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is
$L^p$
-boundedness on a domain and its quotient by a finite group. The range of p for which the Bergman projection is 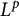 $L^p$
-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
$L^p$
-bounded on our class of Reinhardt domains is found to shrink as the complexity of the domain increases .
Chase Bender was supported by a Student Research and Creative Endeavors grant from Central Michigan University.
Debraj Chakrabarti was partially supported by National Science Foundation grant DMS-1600371.