Article contents
Modular Abelian Varieties Over Number Fields
Published online by Cambridge University Press: 20 November 2018
Abstract
The main result of this paper is a characterization of the abelian varieties 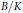 $B/K$ defined over Galois number fields with the property that the
$B/K$ defined over Galois number fields with the property that the  $L$ -function
$L$ -function 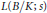 $L\left( B/K;\,s \right)$ is a product of
$L\left( B/K;\,s \right)$ is a product of  $L$ -functions of non-
$L$ -functions of non- 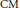 $\text{CM}$ newforms over
$\text{CM}$ newforms over 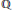 $Q$ for congruence subgroups of the form
$Q$ for congruence subgroups of the form 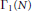 ${{\Gamma }_{1}}\,\left( N \right)$ . The characterization involves the structure of End
${{\Gamma }_{1}}\,\left( N \right)$ . The characterization involves the structure of End 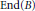 $\left( B \right)$ , isogenies between the Galois conjugates of
$\left( B \right)$ , isogenies between the Galois conjugates of  $B$ , and a Galois cohomology class attached to
$B$ , and a Galois cohomology class attached to 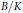 $B/K$ .
$B/K$ .
We call the varieties having this property strongly modular. The last section is devoted to the study of a family of abelian surfaces with quaternionic multiplication. As an illustration of the ways in which the general results of the paper can be applied, we prove the strong modularity of some particular abelian surfaces belonging to that family, and we show how to find nontrivial examples of strongly modular varieties by twisting.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
- 4
- Cited by

