Hostname: page-component-7f64f4797f-bnl7t Total loading time: 0 Render date: 2025-11-04T12:06:27.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone Paths on Zonotopes and Oriented Matroids

Published online by Cambridge University Press:  20 November 2018

Christos A. Athanasiadis  and
Francisco Santos
Christos A. Athanasiadis
Affiliation:
Department of Mathematics, Royal Institute of Technology, S-100 44 Stockholm, Sweden. email: athana@math.kth.se
Francisco Santos
Affiliation:
Departamento de Matemàticas, Estadística y Computación, Universidad de Cantabria, Santander, E-39005, Spain. email: santos@matesco.unican.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Monotone paths on zonotopes and the natural generalization to maximal chains in the poset of topes of an oriented matroid or arrangement of pseudo-hyperplanes are studied with respect to a kind of local move, called polygon move or flip. It is proved that any monotone path on a 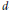$d$ -dimensional zonotope with $n$ generators admits at least 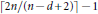$\left\lceil 2n/\left( n-d+2 \right) \right\rceil -1$ flips for all 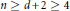$n\ge d+2\ge 4$ and that for any fixed value of 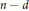$n-d$ , this lower bound is sharp for infinitely many values of $n$ . In particular, monotone paths on zonotopes which admit only three flips are constructed in each dimension 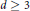$d\ge 3$ . Furthermore, the previously known 2-connectivity of the graph of monotone paths on a polytope is extended to the 2-connectivity of the graph of maximal chains of topes of an oriented matroid. An application in the context of Coxeter groups of a result known to be valid for monotone paths on simple zonotopes is included.

Keywords

52C3552B1252C4020F55

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 6 , 01 December 2001 , pp. 1121 - 1140
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Athanasiadis, C. A., Edelman, P. H. and Reiner, V., Monotone paths on polytopes. Math. Z. 235(2000), 315–334.Google Scholar
[2] Barnette, D., Graph theorems for manifolds. Israel J. Math. 16(1973), 62–72.Google Scholar
[3] Billera, L. J. and Sturmfels, B., Fiber polytopes. Ann. of Math. 135(1992), 527–549.Google Scholar
[4] Billera, L. J., Kapranov, M. M. and Sturmfels, B., Cellular strings on polytopes. Proc. Amer. Math. Soc. 122(1994), 549–555.Google Scholar
[5] Björner, A., Vergnas, M. Las, Sturmfels, B., White, N. and Ziegler, G. M., Oriented Matroids. Encyclopedia Math. Appl. 46, Cambridge University Press, Cambridge, 1993; second edition, 1999.Google Scholar
[6] Bourbaki, N., Groupes et algébres de Lie. Ch. IV–VI, Hermann, Paris, 1968.Google Scholar
[7] Cordovil, R. and Fukuda, K., Oriented matroids and combinatorial manifolds. European J. Combin. 14(1993), 9–15.Google Scholar
[8] Cordovil, R. and Moreira, M. L., A homotopy theorem on oriented matroids. Discrete Math. 111(1993), 131–136.Google Scholar
[9] Deligne, P., Les immeubles des groupes de tresses généralisés. Invent. Math. 17(1972), 273–302.Google Scholar
[10] Edelman, P. H., A partial order on the regions of ℝ n dissected by hyperplanes. Trans. Amer. Math. Soc. 283(1984), 617–631.Google Scholar
[11] Edelman, P. H. and Reiner, V., personal communication, 1999.Google Scholar
[12] Humphreys, J. E., Reflection groups and Coxeter groups. Cambridge Stud. Adv. Math. 29, Cambridge University Press, Cambridge, England, 1990.Google Scholar
[13] Orlik, P. and Terao, H., Arrangements of Hyperplanes. Grundlehren Math. Wiss. 300, Springer-Verlag, New York, 1992.Google Scholar
[14] Reiner, V., The generalized Baues problem. In New Perspectives in Algebraic Combinatorics (eds. Billera, L. J. et al.), MSRI Book Series 38, Cambridge University Press, New York, 1999, 293–336.Google Scholar
[15] Santos, F., A point set whose space of triangulations is disconnected. J. Amer. Math. Soc. 13(2000), 611–637.Google Scholar
[16] Ziegler, G. M., Lectures on Polytopes. Graduate Texts in Math. 152, Springer-Verlag, New York, 1995.Google Scholar