Article contents
Non-stable K1-functors of Multiloop Groups
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 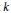 $k$ be a field of characteristic 0. Let
$k$ be a field of characteristic 0. Let 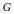 $G$ be a reductive group over the ring of Laurent polynomials
$G$ be a reductive group over the ring of Laurent polynomials 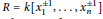 $R\,=\,k\left[ x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1} \right]$ . Assume that
$R\,=\,k\left[ x_{1}^{\pm 1},\ldots ,x_{n}^{\pm 1} \right]$ . Assume that 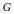 $G$ contains a maximal
$G$ contains a maximal 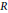 $R$ -torus, and that every semisimple normal subgroup of
$R$ -torus, and that every semisimple normal subgroup of 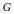 $G$ contains a two-dimensional split torus
$G$ contains a two-dimensional split torus 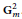 $\mathbf{G}_{m}^{2}$ . We show that the natural map of non-stable
$\mathbf{G}_{m}^{2}$ . We show that the natural map of non-stable 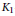 ${{K}_{1}}$ -functors, also called Whitehead groups,
${{K}_{1}}$ -functors, also called Whitehead groups, 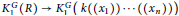 $K_{1}^{G}\left( R \right)\,\to \,K_{1}^{G}\left( k\left( \left( {{x}_{1}} \right) \right)\cdots \left( \left( {{x}_{n}} \right) \right) \right)$ is injective, and an isomorphism if
$K_{1}^{G}\left( R \right)\,\to \,K_{1}^{G}\left( k\left( \left( {{x}_{1}} \right) \right)\cdots \left( \left( {{x}_{n}} \right) \right) \right)$ is injective, and an isomorphism if 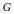 $G$ is semisimple. As an application, we provide a way to compute the difference between the full automorphism group of a Lie torus (in the sense of Yoshii–Neher) and the subgroup generated by exponential automorphisms.
$G$ is semisimple. As an application, we provide a way to compute the difference between the full automorphism group of a Lie torus (in the sense of Yoshii–Neher) and the subgroup generated by exponential automorphisms.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 7
- Cited by

