Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T19:18:29.596Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Caradus Class 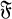of BoundedLinear Operators on a Complex Banach Space

Published online by Cambridge University Press:  20 November 2018

A. F. Ruston
A. F. Ruston*
Affiliation:
University College of North Wales, Bangor, Caernarvonshire
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. In a recent paper (1) on meromorphic operators, Caradus introduced the class 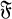of bounded linear operators on a complex Banach space X. A bounded linear operator T is put in the class 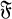if and only if its spectrum consists of a finite number of poles of the resolvent of T. Equivalently, T is in 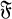if and only if it has a rational resolvent (8, p. 314).

Some ten years ago (in May, 1957), I discovered a property of the class g which may be of interest in connection with Caradus' work, and is the subject of the present note.

2. THEOREM. Let X be a complex Banach space. If T belongs to the class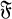, and the linear operator S commutes with every bounded linear operator which commutes with T, then there is a polynomial p such that S = p(T).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 592 - 594
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Caradus, S. R., On meromorphic operators. I, Can. J. Math. 19 (1967), 723–736 Google Scholar
2. Day, M. M., Normed linear spaces (Springer-Verlag, Berlin, 1958).Google Scholar
3. Dunford, N. and Schwartz, J. T., Linear operators. I. General theory (Interscience, New York, 1958).Google Scholar
4. Frôberg, C.-E., Introduction to numerical analysis, pp. 146–148 (Addison-Wesley, Reading, Massachusetts, 1965).Google Scholar
5. Hamming, R. W., Numerical methods for scientists and engineers, pp. 96–97 (McGraw-Hill, New York, 1962).Google Scholar
6. Jeffreys, H. and Jeffreys, B. S., Methods of mathematical physics, p. 246 (Cambridge, at the University Press, 1946).Google Scholar
7. Ruston, A. F., On the Fredholm theory of integral equations for operators belonging to the trace class of a general Banach space, Proc. London Math. Soc. (2) 53 (1951), 109–124.Google Scholar
8. Taylor, A. E., Introduction to functional analysis (Wiley, New York, 1958).Google Scholar