No CrossRef data available.
Article contents
On the Absolute Cesaro Summability of Negative Order of a Series Associated with the Conjugate Series of a Fourier Series
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
1. Definition. Let λ ≡ λ(ω) be continuous, differentiable, and monotonie increasing in (0, ∞) and let it tend to infinity as ω → ∞. A series 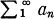 an is summable |R, λ, r|, where r > 0, if
an is summable |R, λ, r|, where r > 0, if
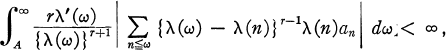
where A is a fixed positive number (6, Definition B).
Let f(t) be a periodic function with period 2π and Lebesgue integrable over (–π, π) and let
1.1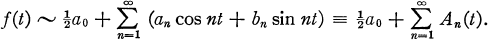
The series conjugate to (1.1), at t = x, is
1.2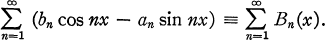
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1969
References
1.
Bosanquet, L. S. and Hyslop, J. M., On the absolute summability of the allied series of a Fourier Series, Math. Z.
42 (1937), 489–512.Google Scholar
2.
Chandrasekharan, K., The second theorem of consistency for absolutely summable series, J. Indian Math. Soc. (N.S.)
6 (1942), 168–180.Google Scholar
3.
Hardy, G. H., Notes on some points in the integral calculus. LXVII: The arithmetic mean of a Fourier constant, Messenger of Math.
58 (1928), 50–52.Google Scholar
4.
Hyslop, J. M., The absolute summability of series by Rieszian means, Proc. Edinburgh Math. Soc. (2) 5 (1936), 46–54.Google Scholar
5.
Mazhar, S. M., A Tauberian theorem for absolute summability, Indian J. Math.
1 (1959), 69–76.Google Scholar
6.
Mohanty, R., On the absolute Riesz summability of Fourier series and allied series, Proc. London Math. Soc. (2) 52 (1951), 295–320.Google Scholar
7.
Mohanty, R. and Misra, B., On absolute logarithmic summability of a sequence related to a Fourier series, Tôhoku Math. J. (2) 6 (1954), 5–12.Google Scholar
8.
Mohanty, R. and Mahapatra, S., On the absolute logarithmic summability of a Fourier series and its differentiated series, Proc. Amer. Math. Soc.
7 (1956), 254–259.Google Scholar
9.
Mohanty, R. and Ray, B. K., On the behaviour of a series associated with the conjugate series of a Fourier series, Can. J. Math.
21 (1969), 535–551.Google Scholar
10.
Varshney, O. P., On the absolute harmonic summability of a series related to a Fourier series, Proc. Amer. Math. Soc.
10 (1959), 784–789.Google Scholar

