Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-19T07:14:06.976Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Group of Homeomorphisms of the Real Line That Map the Pseudoboundary Onto Itself

Published online by Cambridge University Press:  20 November 2018

Jan J. Dijkstra  and
Jan van Mill
Jan J. Dijkstra
Affiliation:
Faculteit der Exacte Wetenschappen / Afdeling Wiskunde, Vrije Universiteit, De Boelelaan 1081, 1081 HV Amsterdam, The Netherlands e-mail: dijkstra@cs.vu.nlvanmill@cs.vu.nl
Jan van Mill
Affiliation:
Faculteit der Exacte Wetenschappen / Afdeling Wiskunde, Vrije Universiteit, De Boelelaan 1081, 1081 HV Amsterdam, The Netherlands e-mail: dijkstra@cs.vu.nlvanmill@cs.vu.nl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we primarily consider two natural subgroups of the autohomeomorphism group of the real line 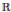$\mathbb{R}$, endowed with the compact-open topology. First, we prove that the subgroup of homeomorphisms that map the set of rational numbers $\mathbb{Q}$ onto itself is homeomorphic to the infinite power of $\mathbb{Q}$ with the product topology. Secondly, the group consisting of homeomorphisms that map the pseudoboundary onto itself is shown to be homeomorphic to the hyperspace of nonempty compact subsets of $\mathbb{Q}$ with the Vietoris topology. We obtain similar results for the Cantor set but we also prove that these results do not extend to 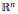${{\mathbb{R}}^{n}}$ for 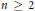$n\ge 2$, by linking the groups in question with Erdős space.

Keywords

57S05homeomorphism groupreal linecountable dense setpseudoboundaryErdős spacehyperspace
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 529 - 547
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Abry, M. and Dijkstra, J. J., On topological Kadec norms. Math. Ann. 332(2005), no. 4, 759–765.Google Scholar
[2] Alexandroff, P., Über nulldimensionale Punktmengen. Math. Ann. 98(1928), no. 1, 89–106.Google Scholar
[3] Arens, R., Topologies for homeomorphism groups. Amer. J. Math. 68(1946), 593–610.Google Scholar
[4] Bessaga, C. and Pełczyński, A., The estimated extension theorem homogeneous collections and skeletons, and their application to the topological classification of linear metric spaces and convex sets. Fund. Math. 69(1970), 153–190.Google Scholar
[5] Bessaga, C. and Pełczyński, A., Selected Topics in Infinite-Dimensional Topology. Mathematical Monographs 58, PWN — Polish Scientific Publishers, Warsaw, 1975.Google Scholar
[6] Bestvina, M. and Mogilski, J., Characterizing certain incomplete infinite-dimensional absolute retracts. Michigan Math. J. 33(1986), no. 3, 291–313.Google Scholar
[7] Brechner, B. L., On the dimensions of certain spaces of homeomorphisms. Trans. Amer. Math. Soc. 121(1966), 516–548.Google Scholar
[8] Brouwer, L. E. J., Some remarks on the coherence type η. Proc. Akad. Amsterdam 15(1913), 1256–1263.Google Scholar
[9] Curtis, D. W. and van Mill, J., Zero-dimensional countable dense unions of Z-sets in the Hilbert cube. Fund. Math. 118(1983), no. 2, 103–108.Google Scholar
[10] Dijkstra, J. J., Fake Topological Hilbert Spaces and Characterizations of Dimension in Terms of Negligibility. CWI Tract 2, Stichting Mathematisch Centrum, Centrum voor Wiskunde en Informatica, Amsterdam, 1984.Google Scholar
[11] Dijkstra, J. J., k-dimensional skeletoids in ℝn and the Hilbert cube. Topology Appl. 19(1985), no. 1, 13–28.Google Scholar
[12] Dijkstra, J. J., On homeomorphism groups of Menger continua. Trans. Amer. Math. Soc. 357(2005), no. 7, 2665–2679.Google Scholar
[13] Dijkstra, J. J., A criterion for Erdőos spaces. Proc. Edinb. Math. Soc. 48(2005), no. 3, 595–601.Google Scholar
[14] Dijkstra, J. J., On homeomorphism groups and the compact-open topology. Amer.Math. Monthly 112(2005), 910–912.Google Scholar
[15] Dijkstra, J. J. and van Mill, J., Homeomorphism groups of manifolds and Erdőos space. Electron. Res. Announc. Amer. Math. Soc. 10(2004), 29–38.Google Scholar
[16] Dijkstra, J. J. and van Mill, J., Erdőos space and homeomorphism groups of manifolds. Preprint: http://www.cs.vu.nl/_dijkstra/research/papers/EH.pdf. Google Scholar
[17] Dijkstra, J. J., van Mill, J., and Steprāns, J., Complete Erdőos space is unstable. Math. Proc. Cambridge Philos. Soc. 137(2004), no. 2, 465–473.Google Scholar
[18] van Engelen, F., Homogeneous Zero-Dimensional Absolute Borel Sets. CWI Tract 27, Stichting Mathematisch Centrum, Centrum voor Wiskunde en Informatica, Amsterdam, 1986.Google Scholar
[19] van Engelen, F., On the homogeneity of infinite products. Topology Proc. 17(1992), 303–315.Google Scholar
[20] Erdőos, P., The dimension of the rational points in Hilbert space. Ann. of Math. 41(1940), 734–736.Google Scholar
[21] Ferry, S., The homeomorphism group of a compact Hilbert cube manifold is an ANR. Ann. of Math. 106(1977), no. 1, 101–119.Google Scholar
[22] Fujita, H. and Taniyama, S., On homogeneity of hyperspace of rationals. Tsukuba J. Math. 20(1996), no. 1, 213–218.Google Scholar
[23] Geoghegan, R. and Summerhill, R. R., Concerning the shapes of finite-dimensional compacta. Trans. Amer. Math. Soc. 179(1973), 281–292.Google Scholar
[24] Geoghegan, R. and Summerhill, R. R., Pseudo-boundaries and pseudo-interiors in Euclidean spaces and topological manifolds. Trans. Amer. Math. Soc. 194(1974), 141–165.Google Scholar
[25] Kechris, A. S., Classical Descriptive Set Theory. Graduate Texts in Mathematics 156, Springer-Verlag, New York, 1995.Google Scholar
[26] Levin, M. and Pol, R., A metric condition which implies dimension ≤ 1. Proc. Amer. Math. Soc. 125(1997), no. 1, 269–273.Google Scholar
[27] Louveau, A. and Saint-Raymond, J., Borel classes and closed games: Wadge-type and Hurewicz-type results. Trans. Amer. Math. Soc. 304(1987), no. 2, 431–467.Google Scholar
[28] Luke, R. and Mason, W. K., The space of homeomorphisms on a compact two-manifold is an absolute neighborhood retract.. Trans. Amer. Math. Soc. 164(1972), 275–285.Google Scholar
[29] Mattila, P., Geometry of Sets and Measures in Euclidean Spaces. Fractals and Rectifiability. Cambridge Studies in Advanced Mathematics 44, Cambridge University Press, Cambridge, 1995.Google Scholar
[30] Michalewski, H., Homogeneity ofK(ℚ). Tsukuba J. Math. 24(2000), 297–302.Google Scholar
[31] van Mill, J., Characterization of a certain subset of the Cantor set. Fund. Math. 118(1983), no. 2, 81–91.Google Scholar
[32] Munkres, J. R., Topology. Second edition. Prentice-Hall, Upper Saddle River, NJ, 2000.Google Scholar
[33] Oversteegen, L. G. and Tymchatyn, E. D., On the dimension of certain totally disconnected spaces. Proc. Amer. Math. Soc. 122(1994), no. 3, 885–891.Google Scholar
[34] Steel, J. R., Analytic sets and Borel isomorphisms. Fund. Math. 108(1980), no. 2, 83–88.Google Scholar
[35] Toruńczyk, H., Homeomorphism groups of compact Hilbert cube manifolds which are manifolds. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 25(1977), no. 4, 401–408.Google Scholar
[36] West, J. E., The ambient homeomorphy of an incomplete subspace of infinite-dimensional Hilbert spaces. Pacific J. Math. 34(1970), 257–267.Google Scholar