Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-29T20:21:14.920Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Product of two Kummer Series

Published online by Cambridge University Press:  20 November 2018

Peter Henrici
Peter Henrici*
Affiliation:
University of California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let a, β, μ, ν, z be complex numbers such that 2μ and 2ν are not negative integers. Using the notation of (4) for generalized hypergeometric series, we set

(1)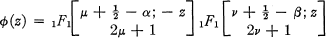 and define an = an(α,β, μ, ν) by

(2)

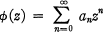
Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 463 - 467
Copyright
Copyright © Canadian Mathematical Society 1958 

Footnotes

Supported by the Office of Ordnance Research, U.S. Army. Reproduction in whole or in part is permitted for any purpose of the United States Government.

References

1. Bailey, W. N., Products of generalized hyper geometric series, Proc. London Math. Soc. (2), 28 (1928), 242-254.Google Scholar
2. Bailey, W. N., Generalized hyper geometric series (Cambridge, 1935).Google Scholar
3. Burchnall, J. L. and Chaundy, T. W., The hyper geometric identities of Cayley, Orr, and Bailey, Proc. London Math. Soc. (2), 50 (1948-49), 56-74.Google Scholar
4. A., Erdélyi et al., Higher transcendental functions, vols. 1 and 2 (New York, 1953 and 1954).Google Scholar
5. Henrici, P., On certain series expansions involving Whittaker functions and Jacobi polynomials, Pacific J. Math., 5 (1955), 725-744.10.2140/pjm.1955.5.725CrossRefGoogle Scholar
6. Henrici, P., On generating functions of the Jacobi polynomials, Pacific J. Math., 5 (1955), 923-931.10.2140/pjm.1955.5.923CrossRefGoogle Scholar