Article contents
On the Restriction to 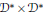 ${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ of Representations of
${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ of Representations of 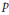 $p$ -adic
$p$ -adic 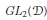 $G{{L}_{2}}(\mathcal{D})$
$G{{L}_{2}}(\mathcal{D})$
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 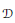 $\mathcal{D}$ be a division algebra over a nonarchimedean local field. Given an irreducible representation
$\mathcal{D}$ be a division algebra over a nonarchimedean local field. Given an irreducible representation  $\pi $ of
$\pi $ of 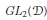 $G{{L}_{2}}(\mathcal{D})$ , we describe its restriction to the diagonal subgroup
$G{{L}_{2}}(\mathcal{D})$ , we describe its restriction to the diagonal subgroup 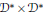 ${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ . The description is in terms of the structure of the twisted Jacquet module of the representation
${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ . The description is in terms of the structure of the twisted Jacquet module of the representation  $\pi $ . The proof involves Kirillov theory that we have developed earlier in joint work with Dipendra Prasad. The main result on restriction also shows that
$\pi $ . The proof involves Kirillov theory that we have developed earlier in joint work with Dipendra Prasad. The main result on restriction also shows that  $\pi $ is
$\pi $ is 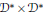 ${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ -distinguished if and only if
${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ -distinguished if and only if  $\pi $ admits a Shalika model. We further prove that if
$\pi $ admits a Shalika model. We further prove that if 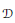 $\mathcal{D}$ is a quaternion division algebra then the twisted Jacquet module is multiplicity-free by proving an appropriate theorem on invariant distributions; this then proves a multiplicity-one theorem on the restriction to
$\mathcal{D}$ is a quaternion division algebra then the twisted Jacquet module is multiplicity-free by proving an appropriate theorem on invariant distributions; this then proves a multiplicity-one theorem on the restriction to 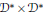 ${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ in the quaternionic case.
${{\mathcal{D}}^{*}}\,\times \,{{\mathcal{D}}^{*}}$ in the quaternionic case.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 6
- Cited by

